使用人工神经网络对心血管疾病进行早期预测
摘要
近年来，死亡率明显上升，而心脏病是导致这一趋势的重要因素。根据加利福尼亚糖尿病研究协会的数据，到2015年，心血管疾病将成为拥有620亿人口的印度的主要死因。心脏向身体其他部位泵血能力的缺陷是心血管疾病的主要原因。医疗行业是一个能够从海量数据和分析洞察中极大受益的典型领域。未来，提取医疗数据以预测和治疗由心脏病发作引起的高死亡率将变得愈发重要。人类每天产生数以太字节计的数据。只有通过高质量的服务才能避免具有严重后果的医疗错误。医院可以通过使用决策支持系统来降低昂贵临床测试的费用。现代医院使用医院信息系统来跟踪患者记录。医疗保健领域产生了大量数据，但其中很少部分被真正有效利用。采用新策略以降低成本并准确预测心脏病变得至关重要。为了确定哪些机器学习和深度学习方法在预测和分类心脏疾病方面最为有效和准确，本文回顾了该主题的现有文献，并进而尝试识别最可能导致心脏病的因素。本研究提出并建模了一种人工神经网络方法，用于识别潜在的心血管疾病风险因素。在本研究中，我们分析并展示了风险属性之间的各种完全和部分相关性。此外，还分析了多个风险变量，以生成最可能导致心血管疾病的预测风险特征列表。
关键词 ：冠心病，人工神经网络，完全性心脏传导阻滞，反向传播
1 引言
现代生活节奏紧张，这可能导致许多人感到焦虑、烦躁和压力。脉率（每分钟心跳次数）和血压（BP；以英寸汞柱或毫米汞柱以及数十或数百毫米汞柱为单位）在个体之间差异很大，通常在120/80和140/90之间。心脏病是全世界任何人群中导致死亡的主要原因。“Cardio”是心脏的医学术语。心血管疾病描述的是一组与心脏相关的病症。
不同类型的心脏病如下：
- 先天性心脏病
- 心律失常
- 冠状动脉疾病
- 扩张型心肌病
- 心肌梗死
- 心力衰竭
- 肥厚型心肌病
- 二尖瓣反流
通常所说的神经网络是指一组神经元。人工神经网络（ANN）是一种设计成类似人类神经系统的计算机网络。它是一个包含多个层次的网络，每一层包含输入神经元、隐藏神经元或输出神经元 [1,2]。对于传统计算机或人类都难以完成的任务，人工神经网络是一种有前景的替代方案 [3]。它们被用于非参数预测，能够从周围环境中获取信息，存储这些信息，并在需要时再次应用。简而言之，人工神经网络由人工神经元和其他数据组成的网络构成，以联结主义方式组织的处理单元 [4]。通过在学习和训练过程中不断更新联结权重的系统，它在模式匹配、预测、识别等方面表现出色。因此，它能够建立所提供数据与最终分类结果之间的关联。在人工神经网络的发展训练阶段，它们本质上是自适应网络，持续调整其内部结构以及在整个系统中流动的信息 [5]。人工神经网络是解决模式分类和预测问题的强大工具。以下是人工神经网络的一些主要优势：
- 首先，权重的增加使它们更能抵抗噪声。
- 其次，人工神经网络（ANN）的性能总是可以更优，因为它在训练过程中也在持续学习。
- 第三，人工神经网络（ANN）可以并行运行以提高效率。
- 当进行适当的训练时，错误率较低。
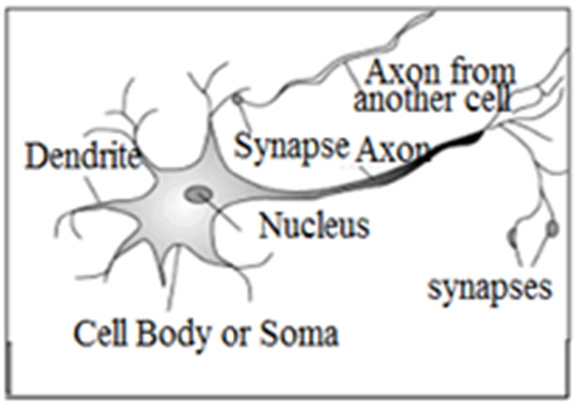
人工神经网络是一种复杂的数据处理架构，包含许多独立的节点。它们之间的关系非常复杂。每个处理元件都有一个输出连接，该连接会分出多个分支，所有分支都传递相同的信号。生物神经元在图1中用简化模型表示。
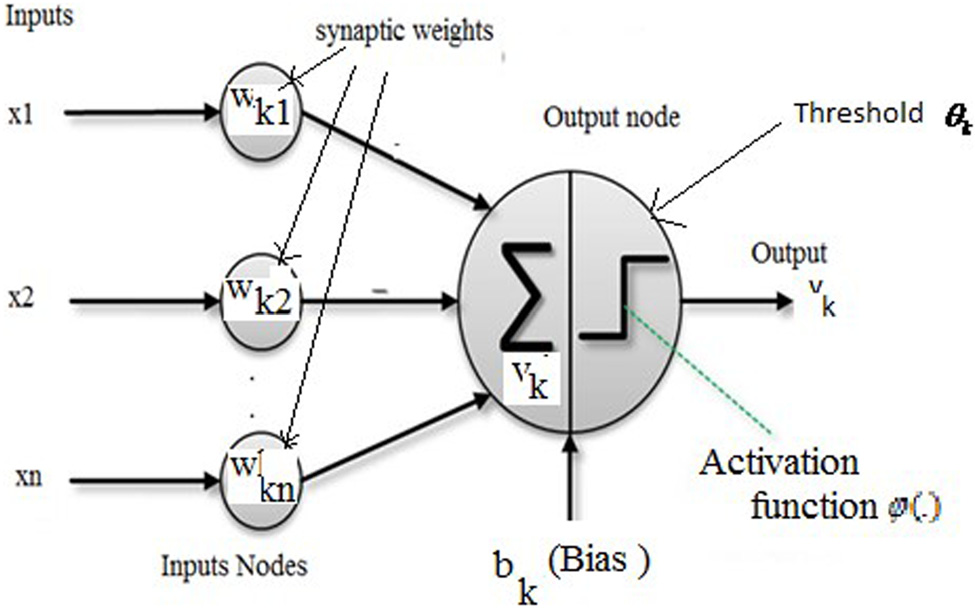
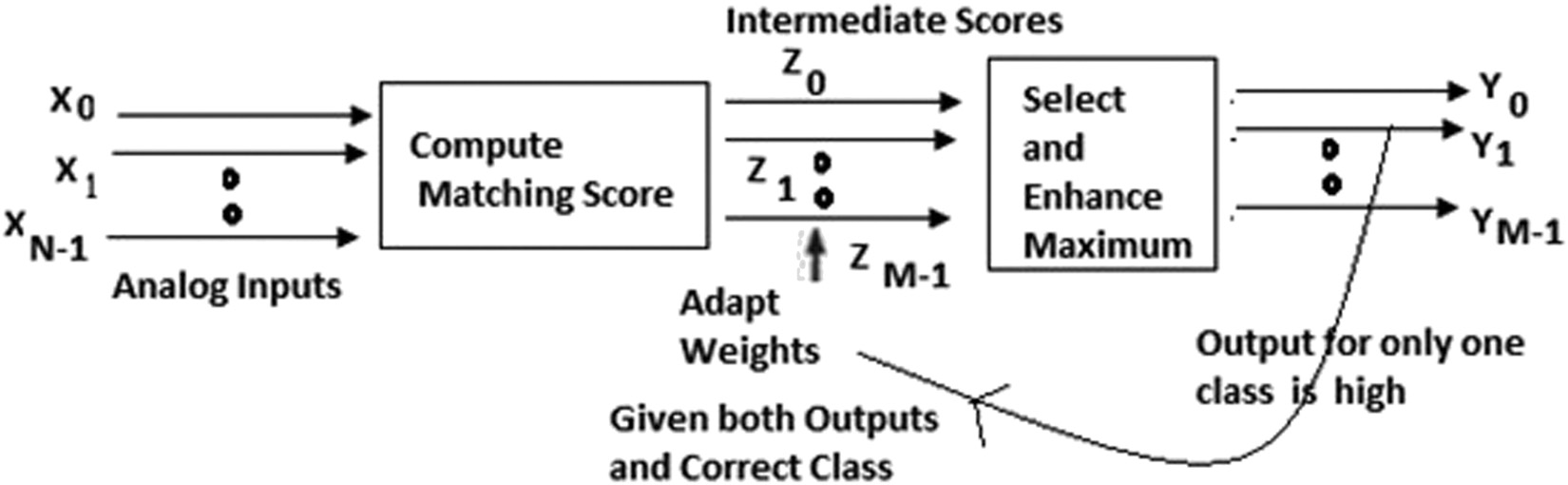
McCulloch–Pitts 神经元 (1943)[6]是人工神经网络的基本构建模块，正如神经元是生物学中的基本计算单元一样。人工神经网络通常使用 McCulloch–Pitts 神经元模型 (图2) 来构建。
1.1 多层感知机（MLP）
该多层感知机（MLP）架构为当前的人工神经网络（ANN）设计提供了灵感。多层感知机（MLP）是一种具有两个隐含层的人工神经网络（ANN），由许多相互连接的人工神经元层组成。这些层级是隐藏的，因为它们位于输入层和输出层之间。如果添加一个或多个隐含层，该网络可被训练以获取高阶统计信息-order statistics if oneor more hiddenlayers are added[7]。
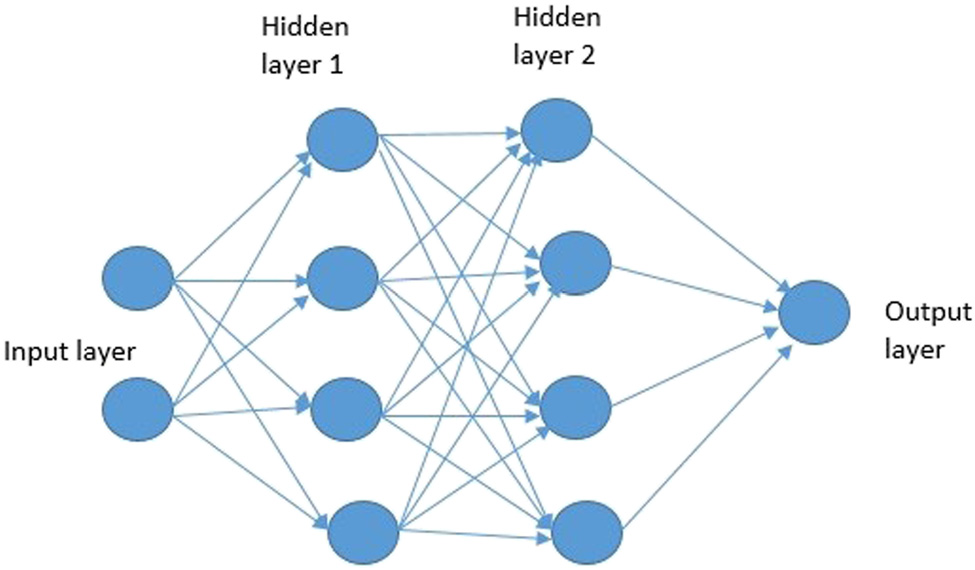
在具有单个隐含层的多层感知机中，输出表达式由以下方程表示：
$$
o = \sum_{i=1}^{N} \beta_i g(w_i x + b_i)
$$
其中 $\beta_i$ 是第i个隐层神经元的质量，$g(.)$ 是激活函数，$w_i$ 是层间的连接权重矩阵，$x$ 是输入模式向量，而 $b_i$ 是与连接至第i个隐层神经元的权值矩阵相关的偏置，共使用了 N个这样的神经元。
“训练”指的是对标准多层感知机的权重和偏置进行微调的过程。对于多层感知机而言，误差反向传播算法是一种常用的选择。为此，必须将误差校正通过网络的神经元进行反向传播。为了使用人工神经网络进行分类，必须首先训练网络，以生成用于标注所有可能网络输出的最优决策规则。显然，该训练过程应旨在降低如下公式所示的风险函数：[7,8]
$$
R = \frac{1}{2} \sum_j (d_j - F(x_j))^2
$$
其中 $d_j$ 表示你希望原型向量 $x_j$ 生成的输出模式，而在训练网络时，N代表训练样本的总数。
决策规则表示为网络的输出，如以下公式所示：
$$
d_k = F(x_j)
$$
1.2 相关工作
如今，许多研究采用机器学习、深度学习和数据挖掘来预测疾病，但结果因研究者的方法而异。
利用数据挖掘预测心血管疾病-的现有研究由Sahaya Anthony Xavier 等人进行了分析。 [9]。心脏事件的预测是数据挖掘方法的常见应用。Weka、Rapid Miner、Datamelt、Apache Mahout、Rattle、KEEL、R 数据挖掘以及等等，以及所使用的数据库和工具（例如来自UCI仓库的心脏病数据集）均有提及。他们的研究得出结论：采用统一方法能够提高预测质量。然而，通过混合使用两种或多种算法，可以大幅提高心脏病预测的准确性。
Chaurasia 和 Pal 提倡使用数据挖掘方法[10]来检测人类的心血管疾病。利用 WEKA 机器学习软件实现了 J48、朴素贝叶斯和装袋算法等数据挖掘技术。在 UCI 进行的研究是在机器学习实验室中开展的。该心脏病数据集中包含 313 个描述性属性以及 13 个诊断/预测属性。-朴素贝叶斯的准确率为 82.31%，而 J48 的准确率为 84.35%，装袋算法的准确率为 85.35%。
根据Vembandasamy等人倡导的贝叶斯方法et al。[11]采用朴素贝叶斯算法-该算法。朴素贝叶斯算法基于强烈的独立性原则。在本文中，我们使用了一个著名的500人糖尿病研究数据集。Weka是一种数据挖掘程序，使用70%训练和30%测试数据集进行分类。朴素贝叶斯算法的成功率为86.41%。
拉克希米[12],研究表明，偏最小二乘判别分析方法的准确率达到86.13%，其使用心脏病UCI数据库中的四组数据并维护十种方法。
夏尔马和帕尔马[13]提出采用数据方法来改进心脏病预测数据集。支持向量机(SVM)提供的85%准确率既优越又高效。与顺序支持向量机相比，并行支持向量机实现的准确率显著更高。
阿什维尼·谢蒂 等人[14]使用MATLAB和WEKA工具，通过多种数据挖掘技术进行心脏病预测。混合系统的成功率为91%，而神经网络的成功率为84%。
贝耶内等人[15]使用了多种数据挖掘方法对心脏病进行预测和分析，例如J48、朴素贝叶斯（NB）和支持向量机（SVM）。这些算法取得了更好的结果，进而有助于提升医疗标准，同时减轻个人的经济负担。
1.2.1 人工神经网络训练包含两次“传递”
包括两个步骤：（i）前向计算和（ii）反向计算、误差评估以及连接权重更新。随着训练的进行，希望均方误差 (MSE)将更快地接近目标值 [16]。它们的逻辑进展区域如下。
1.2.1.1 权值矩阵的初始化
如果使用-Sigmoid函数作为激活函数，则权值矩阵“w”应初始化为介于[−1,1]之间的随机值。可通过将权值矩阵在-Sigmoid函数用作激活函数时，将权值矩阵初始化为-范围内的随机值来实现。对于C个类别，“w”是一个[C × P]矩阵，其中P是用于该类别的特征向量的长度 [17,18]。
1.2.1.2 呈现训练样本
作为输入提供给人工神经网络的 $[P_1, P_2, …, P_P]^m$ 和期望的输出为 $[d_1, d_2, …, d_L]^m$，应遵循的步骤如下：
a. 隐含节点的值按如下方式计算：
$$
net_{mj_h} = \sum_{i=1}^{L} w_{ji_h} p_{mi} + \emptyset
$$
b. 然后，我们将按如下方式计算隐含层的输出：
$$
O_{mj_h} = f(net_{mj_h})
$$
其中
$$
f(x) = \frac{1}{1 + e^{-x}} \quad \text{or} \quad f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
$$
c. 按照以下方式确定输出节点的值：
$$
O_{mk_o} = f(net_{mj_o})
$$
i. 前向计算：通过前向计算进行误差计算：
$$
e_{jn} = d_{jn} - O_{jn}
$$
输出层的误差计算如下[18]：
$$
MSE = \frac{1}{2} \sum_{j=1}^{M} \sum_{n=1}^{L} e_{jn}^2
$$
输出层的误差计算如下：
$$
\delta_{mk_o} = O_{mk_o}(1 - O_{mk_o}) e_{mn}
$$
隐含层的误差计算如下-所示 [19]：
$$
\delta_{mk_h} = O_{mk_h}(1 - O_{mk_h}) \sum_j \delta_{mj_o} w_{jk_o}
$$
ii. 权重更新
Eq.(1.10)显示了输出与隐藏层之间的关系。
$$
w_{kj}(t+1) = w_{kj}(t) + \eta \delta_{mj_o} O_{mj_o}
$$
问题是：学习的节奏究竟体现在哪里？
添加动量项($\alpha$)到公式 (1.11)可使学习率更快收敛 $(0 < \eta < 1)$：
$$
w_{kj}(t+1) = w_{kj}(t) + \eta \delta_{mj_o} O_{mj_o} + \alpha (w_{kj}(t) - w_{kj}(t-1))
$$
表达式 (1.12)揭示了隐含层与输入层之间的关系：
$$
w_{jhi}(t+1) = w_{jhi}(t) + \eta \delta_{jhi} P_i
$$
Eq.(1.13)，加上动量项后，如下所示。
$$
w_{ji_h}(t+1) = w_{ji_h}(t) + \eta \delta_{ji_h} P_i + (w_{kj}(t) - w_{kj}(t-1))
$$
一个训练周期是遍历整个训练集一次。上述每个操作都会重复进行，直到均方误差达到预期结果。
2 目标
本研究旨在利用人工神经网络构建一个用于心脏疾病早期预测或诊断的系统或模拟环境。希望该建议的设置能够从现有心血管疾病数据库中挖掘并提取迄今未知的信息。这将有助于医生和护士比基于过时信息的当前系统做出更明智的临床判断。
3 数据收集
本研究中使用的所有医院和护理院均位于印度阿萨姆邦最大城市古瓦哈蒂及其周边地区，该市是整个印度东北部的主要医疗中心-。虽然整体医疗数据库包含76个特征，但本次对心血管疾病-/冠心病 (CVD)/cor-onary heart disease(CHD) 的分析仅使用了其中8个特征，采用人工神经网络方法(表1)。
| 序号 | 属性名称 | 描述 |
|---|---|---|
| 1 | Age | 年龄（岁） |
| 2 | Sex | 男性/女性 |
| 3 | 胸痛（CP） | 典型心绞痛，不典型心绞痛，非心绞痛性疼痛，无症状 |
| 4 | 静息血压（BP） | 静息血糖（毫米汞柱） |
| 5 | 胆固醇 | 血清胆固醇（毫克/分升） |
| 6 | FBS | 空腹血糖（毫克/分升） |
| 7 | 最大心率（THAL） | 达到的最大心率 |
| 8 | 遗传 | 冠状动脉家族史 疾病 |
4 多层感知机
在本研究中，多层感知机主要通过使用MATLAB进行定义fi。以下是ANN中功能层与隐含层之间的关系-隐藏层在人工神经网络中的关系 [20]。
ffnet = newff(输入_数据, 期望_输出 <训练算法 >。
使用
newff()
时的参数如下：
(i) 输入_数据 [X]：此处输入数据使用通过训练数据集的输入矩阵。这主要决定了
new-ff()
的输入数量。
(ii) 期望_输出[T]：训练集中答案以矩阵形式按列编码。对于
newff
，它决定了输出单元的总数 ()。
(iii)
{k1, k2, ..., km}
：它表示每个隐藏层上的节点数量。
(iv)
{f1, f2, ..., fm}
：它代表所有功能层的激活函数。常用的数学运算包括
logsig()
,
tansig()
, 和
purelin()
。
(v) 在这种情况下，输出层的激活函数可以是线性或非线性的。然而，隐含层必须使用非线性激活函数[21,22]。
(vi)
<训练算法>
：nnff() 是在 MATLAB 中实现的训练函数，它有两种主要变体：
(a) 增量式，通过调用
adapt()
来启动学习过程 ()。
(b) 批量式，通过调用
'train()'
开始训练过程。
调用
adapt()
时，参数可以有以下形式：
-
<“learned”>
：它与通过梯度下降法推导出的串行反向传播标准相同。
-
<‘learngdm’>
：它是基于动量的反向传播变体。
-
<‘learngda’>
表示具有可变学习率的变体。
当调用函数
train()
时，此参数的可能取值如下：
-
<‘traingd’>
：它是传统批量式反向传播的梯度下降版本。
-
<‘traingdm’>
：它是动量反向传播变体。
-
<‘trainlm’>
表示基于Levenberg–Marquardt最小化的变体。
反向传播算法是神经网络和人工神经网络中最广泛使用的监督训练算法之一。用于训练神经网络（NNs）和人工神经网络的反向传播算法包括三个步骤：
(i) 前向传播输入训练样本，
(ii) 定位误差并反向传递，以及
(iii) 权重的等量分配。
人工神经网络设置：本研究采用-反向传播算法 [22] 对心血管疾病和冠心病进行评估-冠心病
| 参数名称 | 隐式值 |
|---|---|
| 学习率，lr | 0.01 |
| epoch遍历次数：所需次数 遍历训练集 | 10 |
| 最大误差值（目标） | 0.001 |
| 参数名称 | 隐式值 |
|---|---|
| 学习率，lr | 0.01 |
| 训练周期遍历次数：所需遍历的 遍历训练集 | 01 |
| 动量系数，mc（如果使用‘learngdm’是使用) | 0.9 |
| 参数名称 | 隐式值 |
|---|---|
| 学习率 net.trainParam.lr= | 0.05 |
| 最大迭代次数 net.trainParam.epochs= | 500 |
| 停止条件 net.trainParam.goal= | 0.001 |
| # 使用人工神经网络对心血管疾病进行早期预测 |
5 神经网络规格说明
表5展示了在当前心血管疾病/冠心病数据分析和疾病预测过程中所考虑的人工神经网络参数。
| 参数名称 | 隐式值 |
|---|---|
| 输入数据大小 | 样本向量长度（针对用于训练、验证和测试的数据集） |
| 信噪比 | 0–3 分贝 |
| 人工神经网络类型 | 具有两个隐藏层的多层感知机。第一个隐藏层的长度是特征向量的1.5倍，第二个隐藏层为特征向量的0.75倍。 |
| 人工神经网络训练方法 | 采用Levenberg–Marquardt优化的反向传播 |
| 平均训练周期 | 多层感知机：200–1,000 |
| 均方误差目标 | 10⁻⁴ |
6 结果分析
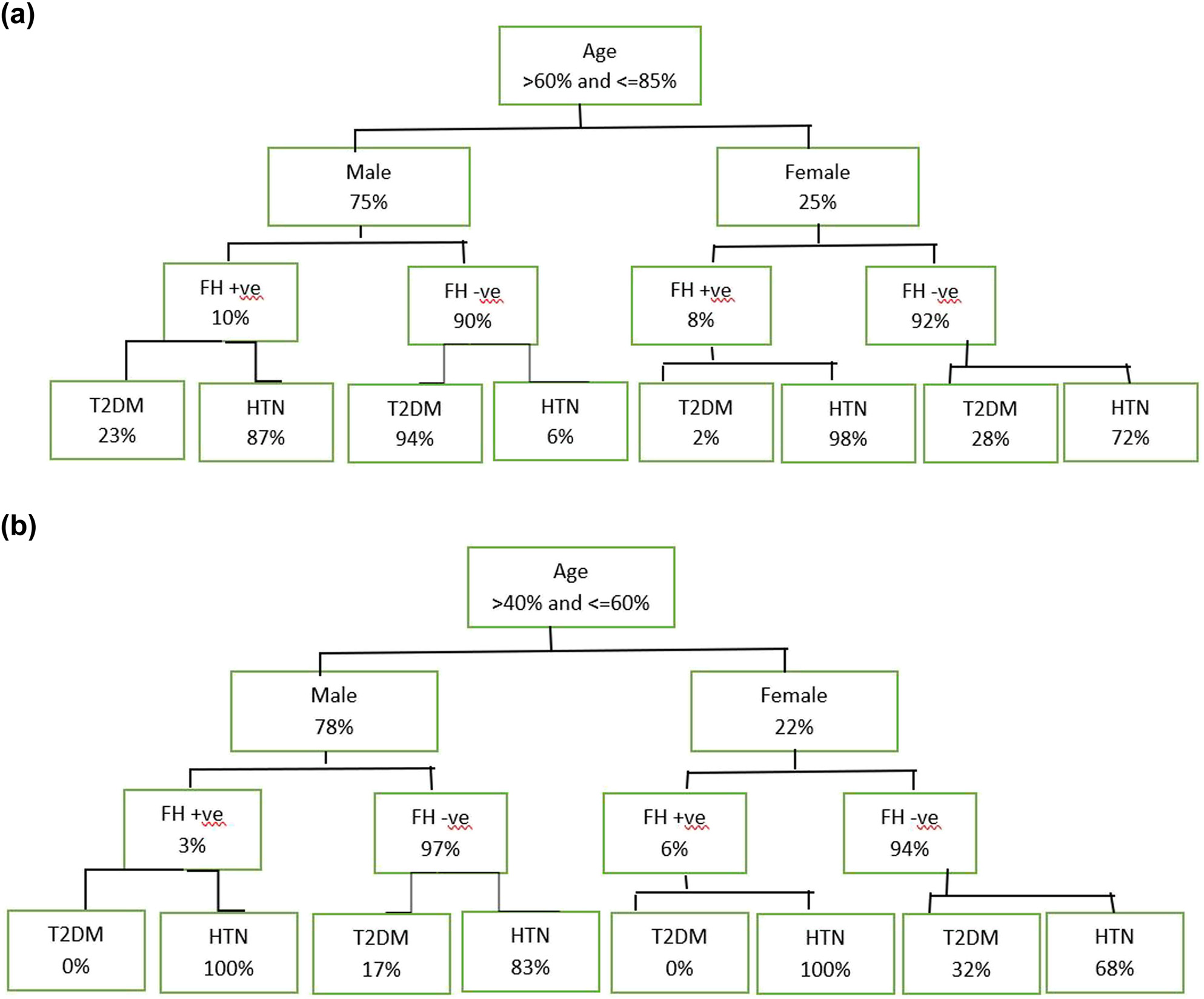
本研究共分析了1500名心脏病患者，以确定人工神经网络在心血管疾病（CVD）和冠心病（CHD）早期阶段的预测和诊断效果。所有患者的病史均来自公共和私人医疗机构。已使用人工神经网络对四个关键心脏特征进行预测：血压（BP）、空腹血糖（FBS）、铊（THAL）和胆固醇（CHOL）- (FBS)、铊（THAL）以及胆固醇(CHOL)[22]。对于特定的心脏状况，性别未被作为优先考虑因素。此外，在当前分析中，年龄和家族史未被纳入心脏疾病的风险因素。图5（a）和（b）展示了年龄、家族史、2型糖尿病、高血压等因素对1500名心脏病患者的影响树状图，分别针对年龄在60至85岁之间的男性和40至60岁之间的女性。
来自1500名心脏病患者的数据被分为三部分，用于训练人工神经网络、验证其性能并评估其表现。
表6详细列出了1500名心脏病患者以及人工神经网络将要预测的疾病。
| 序号 | 疾病 | 全称 |
|---|---|---|
| 1 | CHB | 完全性心脏传导阻滞 |
| 2 | DCM | 扩张型心肌病 |
| 3 | CAD, COAD, M1 | 冠状动脉疾病, 慢性阻塞性气道疾病, 心肌梗死 |
| 4 | ASD | 永久起搏器植入术后，生命终末期 |
| 5 | 风湿性心脏病伴二尖瓣狭窄 | 风湿性心脏病伴二尖瓣狭窄 |
| 6 | SSS | 病态窦房结综合征 |
| 7 | 心房颤动伴缓慢心率 | 心房颤动 |
| 8 | CSA | 慢性稳定性心绞痛 |
| 9 | HOCM | 肥厚型梗阻性心肌病 |
| 10 | ICMP | 缺血性心肌病 |
| 11 | RBBB + LAFB | 右束支传导阻滞 + 左前分支传导阻滞 |
典型的 人工神经网络 如图6所示；它由一个隐含层和一个输出层组成，接收来自血压、空腹血糖、THAL和CHOL的输入(特征向量)。
使用1,050例心脏疾病病例和四个主要属性：血压、空腹血糖、总高血压（THAL）和总胆固醇，对人工神经网络进行训练。在验证测试中，我们使用了15%（225）的数据（血压、空腹血糖、THAL和CHOL），对于人工神经网络的测试，我们使用了剩余的15%（225）数据。
The effectiveness of the 均方误差 was analysed by developing a 回归分析图 with a log sig activation function, as shown in 图7. Within this graph, the 验证值 is 0.061327, the 训练R value is 0.90091, and the test R value is 0.043058. R’s final value is 0.2828. A more trustworthy validation could be found in the results obtained after data 训练 in multiple contexts.
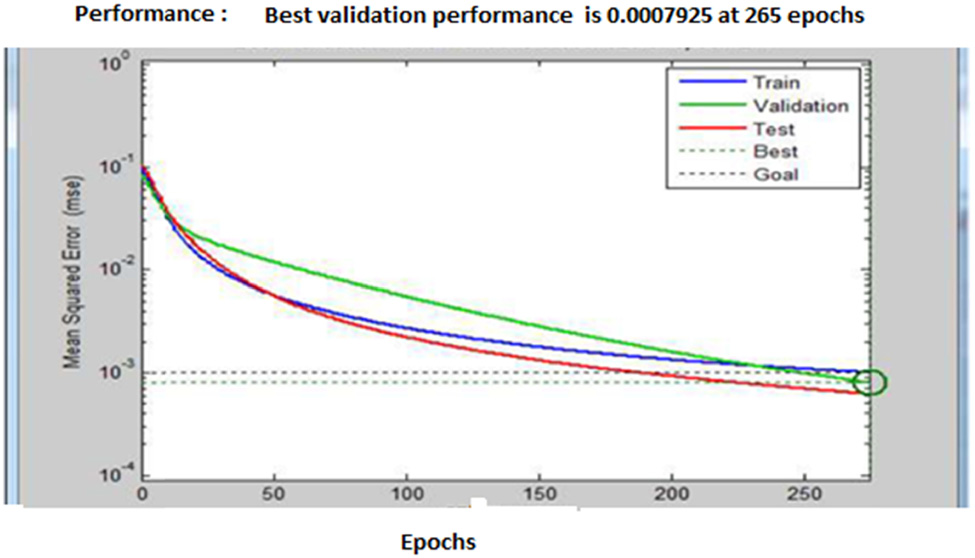
The regression 训练、测试和验证的图表分析如图 7所示。
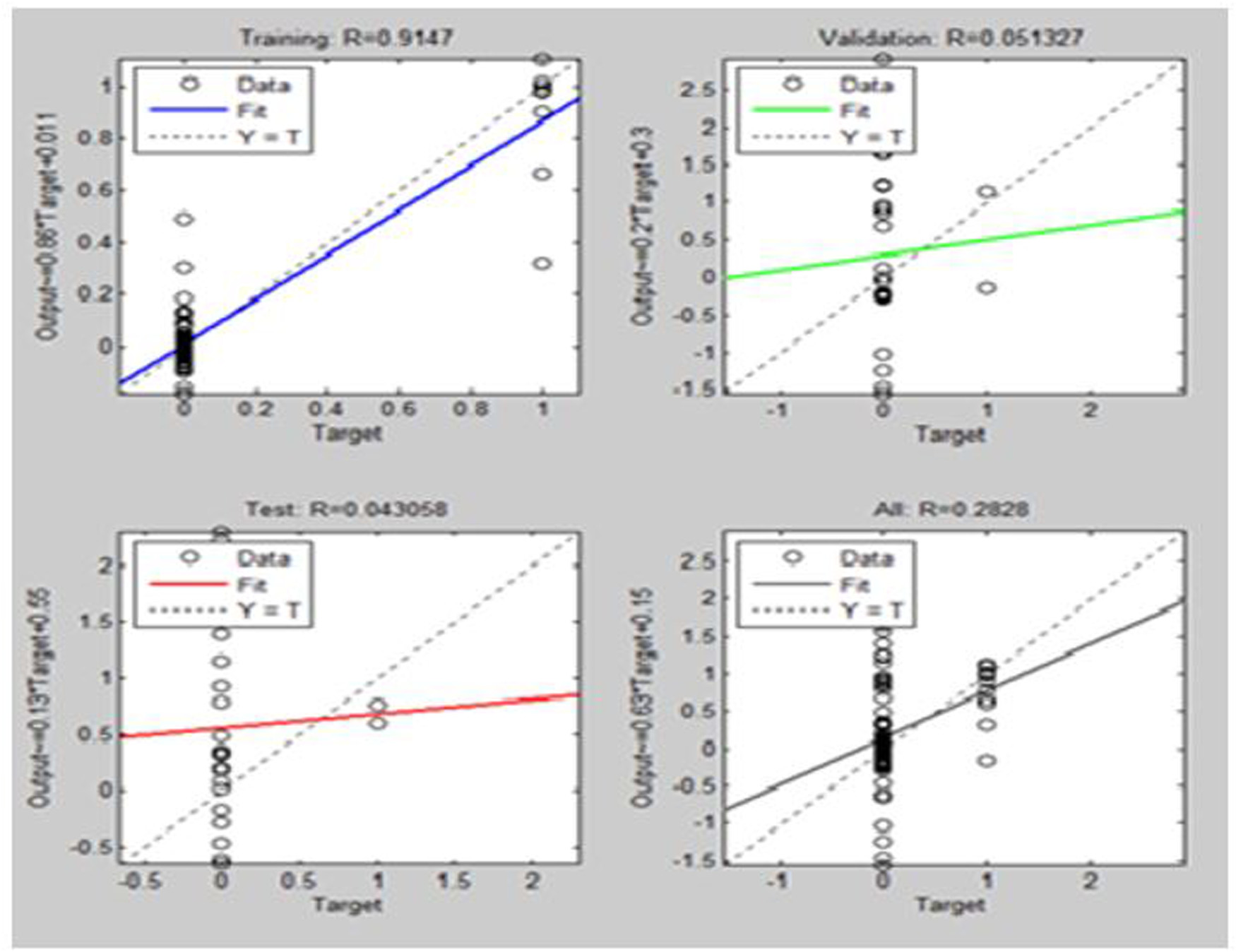
图8(a)和 (b)展示了不同训练成功率下的混淆矩阵。
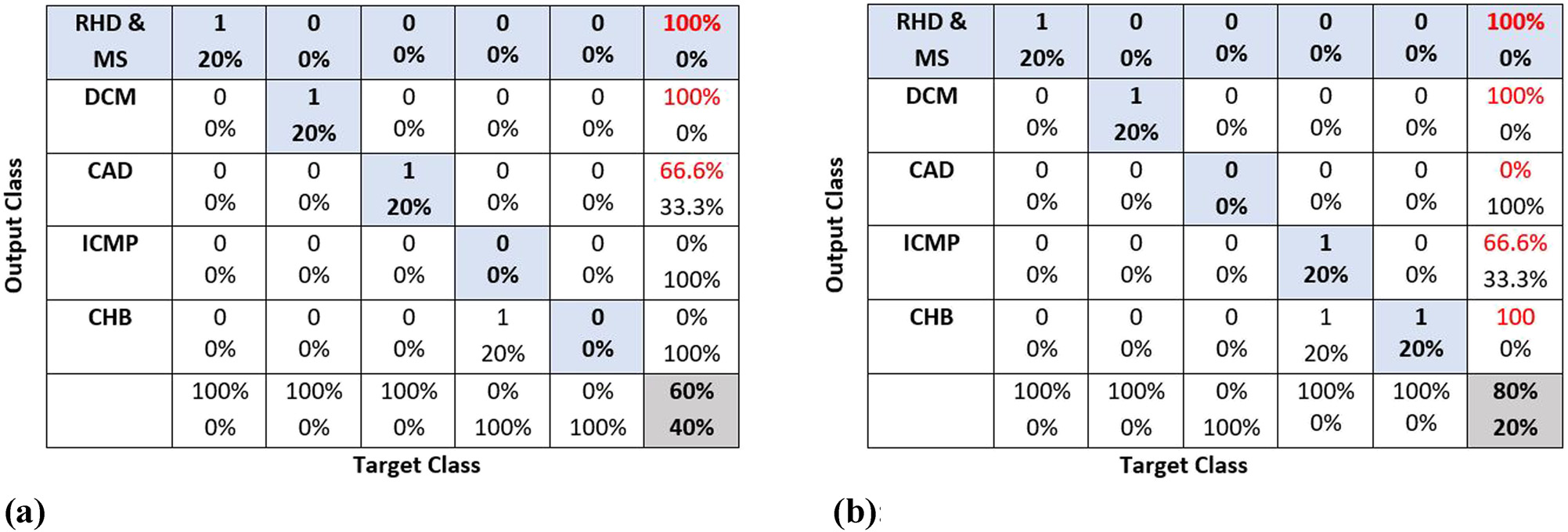
图9(a)和 (b)表示不同测试成功率下的混淆矩阵。
从人工神经网络的这三个阶段——“训练”、“验证”和“测试”的可视化表示中，可以得出以下结论：
首先，正如我们最初所假设的那样，当达到0.001的误差（目标）时，性能最优。
ii. 图8(a)和 (b)展示了混淆矩阵，表明在训练过程中达到了60%到80%的成功率。
iii. 在验证期间观察到约66.7%的成功率，如图9-(b)(b)所示。
iv. 图9(a)显示，在测试期间的识别成功率在无噪声时为80%到60%，在存在2dB噪声时降至20%。
表7 总结了心血管疾病诊断的发病率。
| 疾病名称 | 识别成功率 无噪声(%) | 识别成功率 有噪声(2 dB)(%) |
|---|---|---|
| CHB | 74 | 70 |
| DCM | 91 | 82 |
| CAD, COAD, M1 | 80 | 72 |
| ASD | 78 | 72 |
| 风湿性心脏病伴二尖瓣狭窄 | 92 | 74 |
| SSS | 85 | 73 |
| 心房颤动伴缓慢心率 | 65 | 62.5 |
| CSA | 75 | 62 |
| HOCM | 76 | 70 |
| ICMP | 42 | 38 |
| RBBB + LAFM | 81 | 74 |
计算敏感性(SE)、特异性(SP)和准确率(AC)是评估采用反向传播技术时人工神经网络性能的另一种方法’s 性能的另一种方法-传-播技术[22]。这些特征通过混淆表进行计算。使用1500名患者的健康特征数据中的 70%来训练算法，其余30%用于评估其性能。在表8中，我们可以看到所获得的SE、SP和AC结果的汇总。
| 算法 used | 敏感性（%） | 特异性 (%) | 准确率 (%) |
|---|---|---|---|
| 具有MLPANN的 back 传播 算法 | 82 | 87 | 81 |
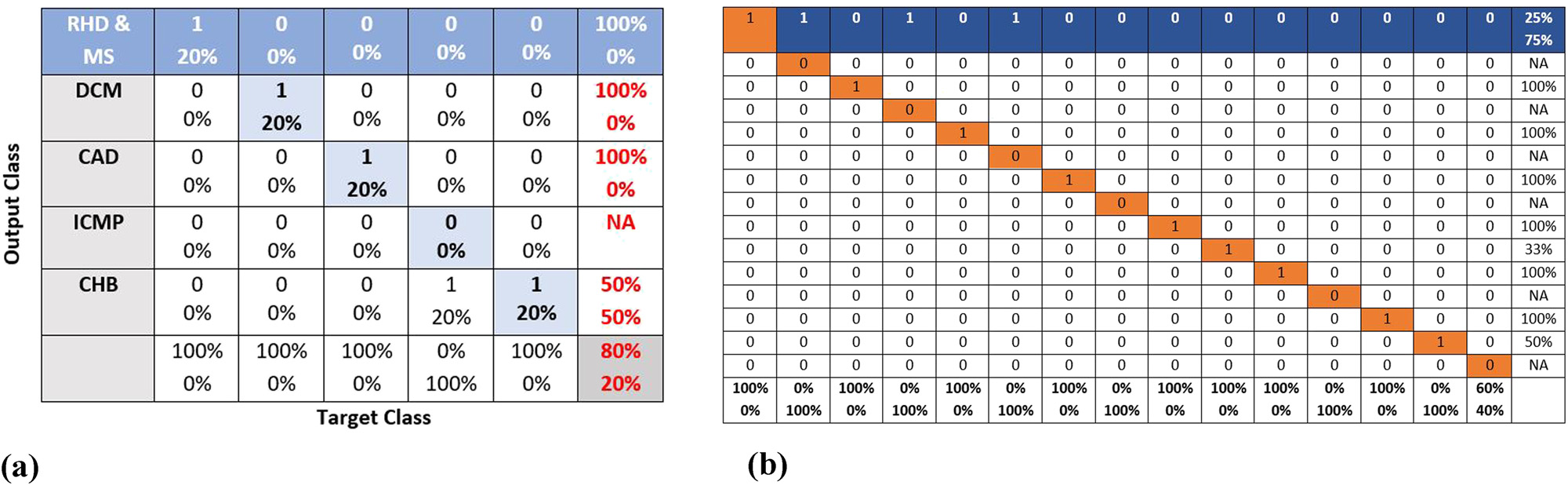准确率为80%的混淆矩阵。(b) 准确率为66.7%的混淆矩阵。)
7 结论与未来工作
本研究的目标是应用人工神经网络技术于包含八个变量的数据集，以开发用于心脏病早期诊断的预测模型。在本次分析中，我们收集并预处理了来自印度阿萨姆邦五家医院的数据：高哈蒂医学院及医院、海亚特医院、GNRC医院、Downtown医院和Narayanan专科超级医院。模型构建过程中采用了多层反向传播 modeling 方法。数据集通过完全和部分相关程序进行了分析。在预处理阶段使用MLP模型识别显著风险变量。在对模型效能进行分析后，确定心血管疾病最关键的指标是血压（BP）、空腹血糖（FBS）、胆固醇（CHOL）和最大心率 (THAL)。因此，在总共八个特征中，四个被确定为显著风险因素。基于这些发现可以明确，采用反向传播算法的基于人工神经网络的心脏病诊断方法在准确率、敏感性和特异性方面优于其他方法。在机器学习中使用反向传播所获得的准确率为81%。为了提高分类准确率并构建能够预测特定类型心脏病的模型，我计划在未来使用更多数据集和算法进行进一步实验。
扫一扫
58
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
