SVD与傅里叶变换分析比对

【2025.5.24补】 附一篇SVD好文https://zhuanlan.zhihu.com/p/29846048https://zhuanlan.zhihu.com/p/29846048

SVD与傅里叶变换均为图像处理的典型方法。

两者在分析方式上有很多相似之处，比如在图像压缩时，两者均可以通过舍弃较小影响因素的分量来实现。下面对两者相似性进行分析。假设读者已经对SVD和傅里叶变换有了足够了解，如果需要复习，请点击

【彻底搞懂】矩阵奇异值分解（SVD） - 知乎

通俗易懂的理解傅里叶变换（一）[收藏] - 知乎

SVD（奇异值分解）

奇异值分解按照固定方式，将矩阵A分解为三个矩阵。从形状上来说，假设A 为M*N，则U形状为M*M,  Σ形状为M*N, V形状为N*N。 在线性代数中，大家学过，方阵代表了同维度的线性变换，由于U、V被限定为正交矩阵，所以从几何意义上来说，U、V代表了旋转、反射变换。中间的Σ矩阵则囊括了 拉伸、升降维的作用。

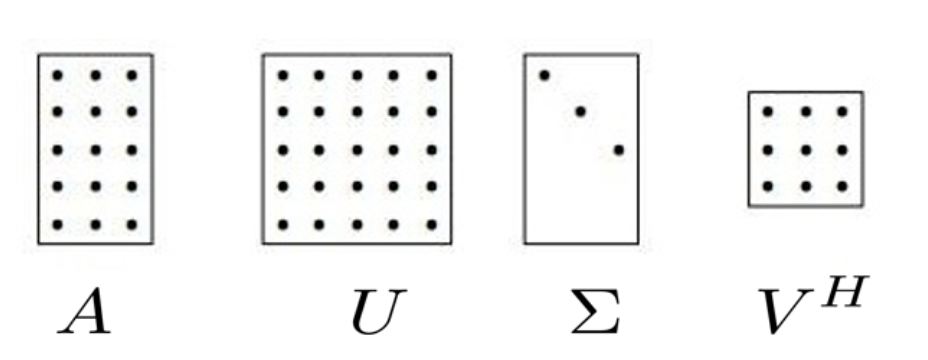那么一个矩阵通过SVD分解后，其线性变换“影响力大小”，实际上是通过Σ矩阵的拉伸表示的，拉伸幅度越大，显然对矩阵的影响力越大。这就是SVD的思想。

Fourier Transformation(傅里叶变换)

傅里叶变换的思想在于“一切皆可正余弦拟合”。也就是说，今天一个矩阵也可使用二维傅里叶变换表示。一维傅里叶变换写成矩阵如下。二维的情况下， f = Q F P, 假设 f 是一个M*N矩阵，则Q为M*M, P 为N*N, F为M*N。 

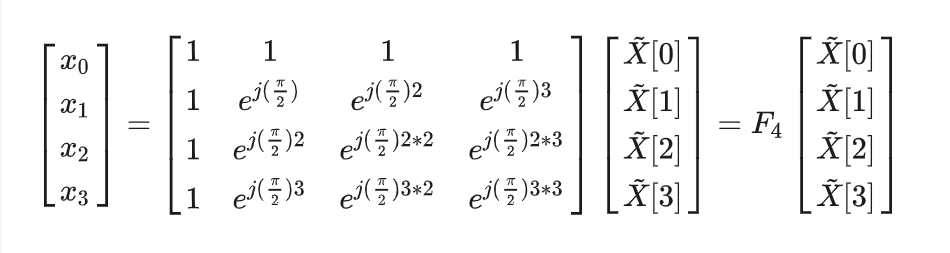
经过傅里叶分解后，一副图像可以表示成M*N 个正余弦正交函数基的形式（当然你也可以写成复数，可以证明，M*N个复数基和上述正余弦基完全等价，这是由欧拉公式指出的）

其中高频信号表征了细节信息，低频信号表征主体信息，那么在进行压缩的时候，自然而然通过舍弃高频信号实现。

对比分析

笔者在初学时希望在数学上找到两者统一，但这样的探索虽然有最终解释，但并不直观，原因是线性代数工具太过强大，能够把两者写成相似形式。 事实上，两者在寻找矩阵的“主要成分”上，思路完全不同。

SVD的思路是，现在读者掌握了一定汽车相关知识，给出一辆特斯拉新款车，希望读者根据效果去分析出其动力系统、供电系统等系统具体如何构成。

傅里叶变换的思路是，给出一个可以构成任何车辆的“万用组件库”，给出一辆特斯拉新款车，希望读者根据组件库像搭积木一样搭出这个车。

所以，一个的思路是“分解”，一个的思路是“合成”；直观上来看，合成也会比分解分析更加容易，以辅助读者记忆。SVD的时间复杂度是O(min(M,N)² · max(M,N))，FFT的时间复杂度是（M*N * log(M*N )）