关于周期函数的假设
数学家认为任意周期函数可以用三角函数的和来逼近,如下图,可以看出他们确实相似
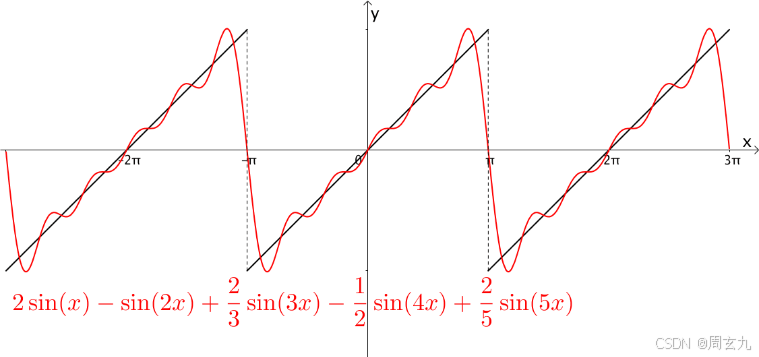
探索的思路
对于Y=C这样的常函数,也是周期函数,所以猜测三角函数累加里边有个常数项 k*cos(0x)
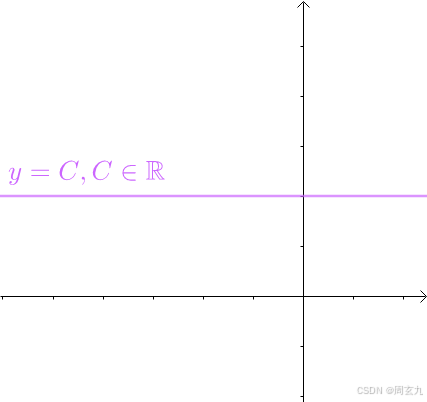
周期相同
现在要拟合一个周期为T的函数,如何让我们三角函数累加的周期也为T呢?
假设sinx 周期为T, 那么sin2x周期也为T,sin3x...sin nx 同理
如果今天要拟合的函数周期为T,那么下边的三角函数
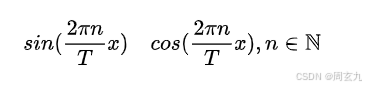
周期都是T
振幅调整
现在得到了一堆周期是2T的函数了,我们需要调整振幅,把他们相加,简单来说,最后调整出来的逼近函数长这样
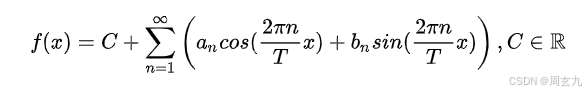
有无穷项的话,就假设是可以完全逼近的。
系数的确定
基本的模拟公式是有了,但是系数C a_n b_n如何去确定呢?
看周期函数内积定义:
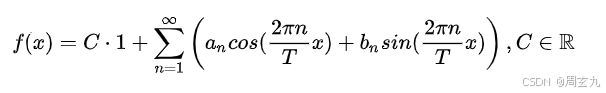
其函数基底为:
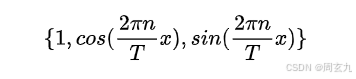
要求的是这三个的系数,应当进行函数内积,除以基底的模
周期函数内积如下定义:

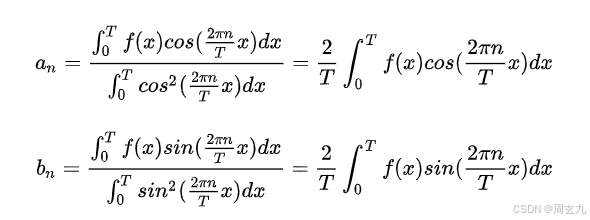
最终得到:
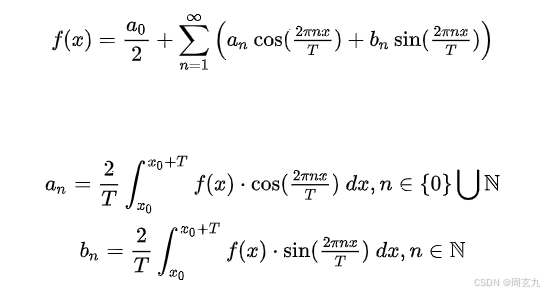




















 6953
6953

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








