Kth Smallest Element in a BST

Problem

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

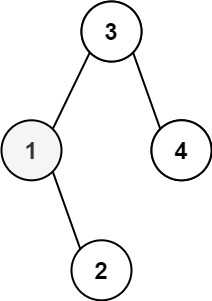
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

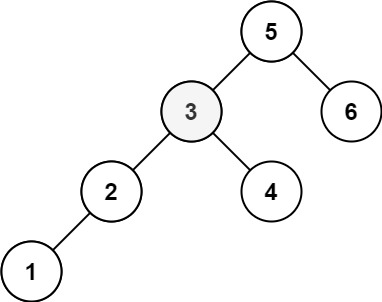
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Intuition

The task is to find the kth smallest value in a binary search tree (BST). In a BST, the left subtree of a node contains only nodes with smaller values, and the right subtree contains only nodes with larger values. Therefore, performing an in-order traversal of the BST will visit the nodes in ascending order. The intuition is to use an iterative in-order traversal (using a stack) and stop when the kth smallest element is encountered.

Approach

Initialization:

Initialize a variable n to count the number of visited nodes.
Initialize an empty stack to perform the iterative in-order traversal.
Start with the root node as the current node (cur).
Iterative In-Order Traversal:

While cur is not None or the stack is not empty:
Push all left children of cur onto the stack until reaching the leftmost node.
Pop a node from the stack (represents the current node in in-order traversal).
Increment the count n by 1.
If n is equal to k, return the value of the current node.
Move to the right child of the current node (cur = cur.right).
Return Result:

Return the kth smallest value found during the traversal.

Complexity

• Time complexity:

The time complexity is O(n), where n is the number of nodes in the binary search tree. In the worst case, the algorithm visits all nodes in the tree during the in-order traversal.

• Space complexity:

The space complexity is O(h), where h is the height of the binary search tree. This is because the maximum depth of the stack is equal to the height of the tree. In the average case, for a balanced binary tree, the height is O(log n), making the space complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a space complexity of O(n). The space complexity is dominated by the depth of the stack during the traversal.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        n = 0
        stack = []
        cur = root

        while cur or stack:
            while cur:
                stack.append(cur)
                cur = cur.left

            cur = stack.pop()
            n += 1
            if n == k:
                return cur.val

            cur = cur.right