Binary Tree Level Order Traversal

最新推荐文章于 2025-07-29 19:56:06 发布

kotic

最新推荐文章于 2025-07-29 19:56:06 发布

阅读量812

点赞数 26

CC 4.0 BY-SA版权

分类专栏： leetcode算法学习文章标签：算法

本文链接：https://blog.youkuaiyun.com/kduduuuw/article/details/135177615

leetcode算法学习专栏收录该内容

71 篇文章

订阅专栏

文章介绍了如何在给定二叉树的根节点时，按层序遍历其节点值。使用广度优先搜索（BFS）方法，通过队列（deque）逐层处理节点，最终返回一个表示层序遍历的二维列表。时间复杂度为O(n)，空间复杂度为O(n)。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Problem

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

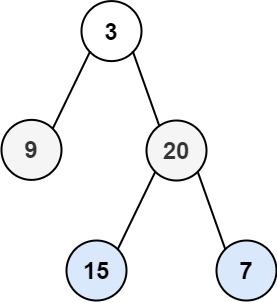
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Intuition

The task is to perform level order traversal on a binary tree, which involves visiting nodes level by level from left to right. The intuition is to use a queue to keep track of the nodes at each level and then process them one level at a time.

Approach

Initialization:

Check if the root is None. If so, return an empty list since there are no nodes to traverse.
Breadth-First Search (BFS):

Use a queue (in this case, a deque) to perform a breadth-first traversal of the binary tree.
Initialize the queue with the root node.
Level Order Traversal:

While the queue is not empty:
Create a temporary list (temp) to store the values of nodes at the current level.
Process all nodes at the current level:
Pop the front node from the queue.
Enqueue its left and right children (if any).
Append the value of the current node to the temp list.
If the temp list is not empty, append it to the final result (stack).
Return Result:

Return the final result, which is a list of lists representing the level order traversal.

Complexity

Time complexity:

The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the traversal.

Space complexity:

The space complexity is O(m), where m is the maximum number of nodes at any level in the binary tree. In the worst case, the maximum number of nodes at any level is the number of leaf nodes, which is at most n/2 in a balanced binary tree. Therefore, the space complexity is O(n/2), which simplifies to O(n) in big-O notation. This is because the space required to store nodes at any level scales with the number of nodes in the tree.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []

        stack = [[root.val]]
        q = deque([root])
        while q:
            temp = []
            for _ in range(len(q)):
                node = q.popleft()
                if node.left:
                    q.append(node.left)
                    temp.append(node.left.val)
                if node.right:
                    q.append(node.right)
                    temp.append(node.right.val)

            if temp:
                stack.append(temp)

        return stack