用于射频电路设计的集成电感器参数化宏建模
F. 帕索斯,1叶洋,2 D. 斯皮纳,2 E. 罗卡,1 R. 卡斯特罗‐L佩斯,1 T. 达恩,2和 F.V. 费尔南德斯 1
塞维利亚大学,微电子研究所 塞维利亚大学,国家微电子中心‐西班牙高等科研理事会, 西班牙塞维利亚;通讯作者:moreira@imse‐cnm.csic.es2信息技术系,ID实验室,根特大学‐伊迈克, 比利时根特
2016年10月24日收到
摘要
如今,参数化宏建模技术被广泛用于描述电磁结构。本文研究了此类参数化宏建模技术在集成电感器设计和射频电路设计中的应用。为了实现这些不同的操作,提出了一种新的建模方法,与先前技术相比,该方法提高了建模精度。新方法针对研究中的器件的独特特性进行了定制。所获得的参数化宏模型随后被用于0.35微米CMOS技术中压控振荡器的综合方法与设计。VC 2017 WileyPeriodicals,Inc.微波与光技术快报 59:1207—1212,2017;在线浏览本文请访问 wileyonlinelibrary.com。DOI10.1002/mop.30498
关键词 :集成电感;参数化宏建模;射频设计;单目标优化;压控振荡器
1. 引言
近年来,由于集成电感器在射频集成电路(RF IC)中具有重要作用,人们为其开发了许多模型。这些模型大多基于集总元件电路,如π型模型[1],、双π型模型[2],和T型模型[3]。然而,这些模型存在精度问题,其建模误差可能超过10% [1,2],或依赖于从已制造样品中提取的复杂技术[3]。
如今,基于参数化宏建模技术的黑箱方法为研究通用的线性无源电磁结构[4—6]提供了一种可靠的解决方案。参数化宏建模技术对这类电磁结构的传输函数进行建模,该传输函数可表示为不同形式(例如导纳、阻抗或散射参数),同时保持因果性、稳定性和无源性等基本物理特性,从而在频域和时域均获得完整的表征[5,6]。
本文的重点是在较大的设计空间内对集成电感器进行建模,开发适用于不同任务(例如电感综合、设计空间探索、电路设计等)的模型。在此情况下,不仅需要准确估计电感器的传输函数(之后可用于推导电感器的S参数并用于电路设计),还必须准确建模电感综合中所使用的主要电感器性能指标(电感L和品质因数Q),因为这些性能指标是设计人员设定优化目标和约束条件所依赖的依据。
在本研究中,结合并改进了文献[5]中提出的参数化宏建模技术以及文献[6],中描述的顺序采样策略,该方法能够在整个设计空间内构建稳定且无源的宏模型,并允许在设计空间的不同区域使用不同级别的精度,从而降低在电感器对电路设计适用性较低区域建模时的计算成本。其次,新的建模技术不仅能够精确估计S参数,还能准确估计电感值L和品质因数Q。通过在顺序采样过程中应用一种新的误差测量策略,实现了对所有性能指标的精度提升,该策略针对集成电感器的独特特性进行了专门设计。
第2节中描述的新建模方法随后在第3节中用于综合压控振荡器(VCO)设计所需的电感器。据作者所知,这是首次将集成电感器的参数化宏建模技术应用于电路设计。最后,第4节得出了结论。
2. 集成电感器的参数化宏建模
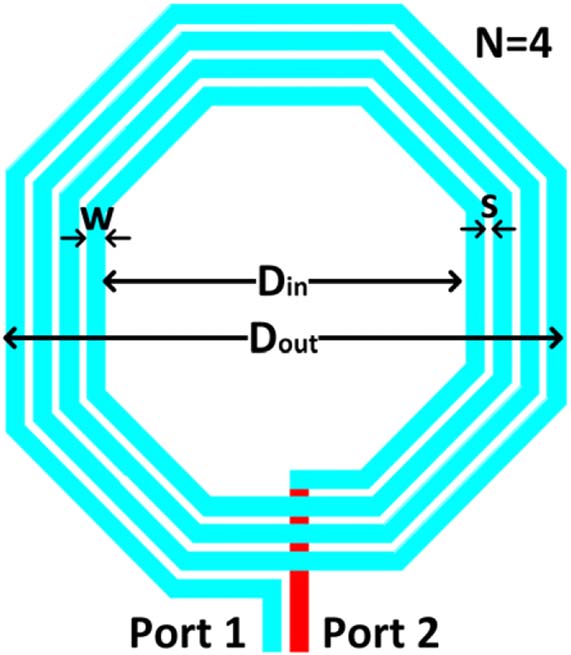
本文所建模的集成螺旋电感器拓扑结构如图1所示。所选工艺为0.35微米CMOS工艺,该工艺可用于电磁仿真所需的工艺信息。本文提出的方法完全独立于电感器拓扑结构和工艺,因此具有很高的灵活性。
针对不同匝数N的电感器分别建立模型。在每种情况下,模型构建的设计空间由内径D in 和线圈宽度w定义,其变化范围如下:D in [10, 300]微米和w [5, 25] 图1八角形五匝螺旋电感器的布局。 [ 彩色图可在 wileyonlinelibrary.com查看 ]
1208微波与光电子技术快报/第59卷,第5期,2017年5月DOI10.1002/mop
微米。电感器的最大面积受限于一个合理较大的外径Dout , 即400微米,而电感器匝间距s保持固定在工艺允许的最小值2.5微米,因为增加该值不会带来性能提升[7]。为了建立模型,对所选样本的S参数在频率范围[0.0001至2.7] 吉赫兹内的17个频率采样点进行评估。所使用的频率采样点数量直接影响建模过程中精度与效率之间的权衡:使用更多的频率点可以提供关于集成电感器行为的更多信息,但由于每个频率采样点都需要进行电磁仿真,因此将导致计算时间增加。
性能参数电感值和品质因数可以从电感器的S参数直接计算得出
$$
Z_{eq} = \frac{(1+S_{11})(1+S_{22}) - S_{12}S_{21}}{(1-S_{11})(1-S_{22}) + S_{12}S_{21}} \times 50
$$
$$
L = \frac{\text{Im}(Z_{eq})}{2\pi f}, \quad Q = \frac{\text{Im}(Z_{eq})}{\text{Re}(Z_{eq})}
$$
(1)
用于模型构建的样本通过电磁仿真器KeysightADS Momentum[8]进行评估。不考虑低于50皮亨的电感值, 因为此类组件在射频设计中不会使用。
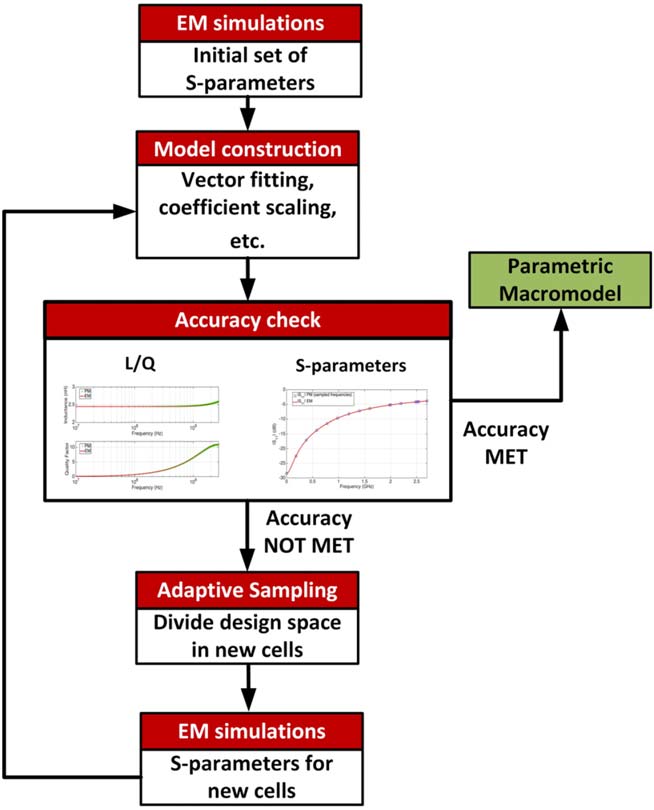
整个建模技术如图2所示的流程图中所示。计算参数化宏模型的第一步是对设计空间角点对应的样本进行电磁场仿真,并利用这些样本构建模型。基于这些初始数据样本,通过矢量拟合(VF)技术[9]建立一组相应的频变有理模型。在此初始阶段之后,将计算出一组稳定且无源的频变有理模型,称为根宏模型。每个根宏模型对应于由其角点定义的设计空间中的单个区域(单元)。随后,计算幅度和频率缩放系统系数
通过优化过程为每个单元的根宏模型计算得出,然后使用正插值算子[5]进行适当的参数化。
随后,检查每个单元的模型精度。如果给定单元的模型误差低于设定的误差阈值,则认为该模型足够精确。如果某个单元的误差高于选定的阈值,则通过自适应采样技术将该单元划分为子单元。在整个子单元中自动递归地应用训练‐验证过程,直到获得一组能够在设计空间的每个单元中满足所需误差阈值的精确局部模型。所有生成的局部模型共同构成整个设计空间的完整参数化宏模型。
很明显,建模过程中的一个关键步骤是选择使用哪种误差度量及其阈值。在本研究中,将比较两种误差测量技术,以证明本文所提出的改进精度检查方法的有效性。在之前报道的模型[5],中,仅考虑了对被研究器件传输函数估计的误差。一种可能的选择是采用在整个频率范围内通过电磁仿真和宏模型得到的S参数之间的最大绝对误差(Mabs),该方法已在文献[5]中用于整个设计空间。然而,电感值(L) 和/或品质因数(Q)的精度可能对S参数估计误差非常敏感。
表1显示了在2.5GHz时,基于一组4936个测试电感(不同于用于模型训练的电感器)计算出的电感值最大相对误差( MRL)和Q的最大相对误差(MRQ),这些模型仅使用S参数的Mabs误差度量构建(我们将此称为模型S)。需要指出的是,对于不同匝数的电感器,可以采用不同的Mabs阈值来实现更高的精度。注意,对于匝数不超过四匝的电感器, MRQ始终高于5%。这一结果证实,S参数估计中的微小误差可能导致例如Q估计中的较大相对误差。
因此,显然必须采用一种新的策略,才能获得准确的电感值和品质因数建模结果。使用以往的技术(如模型S),无法在设计空间的不同区域应用不同的误差度量。
因此,提高模型精度的唯一方法是降低Mabs的误差阈值, 例如从250降至270分贝。然而,这将导致对整个(w,Din)设计空间进行过采样,这不是一种可行的解决方案。
因此,本信函提出的新方法是采用基于S参数以及电感值和品质因数的误差度量,并允许设计者为设计空间的不同区域设置不同的误差度量。通过所提出的方法,我们不仅保证了准确的估计
| N | Mabs (dB) | 模型S MRL(%) | 模型S MRQ(%) | SLQ模型 MRL(%) | SLQ模型 MRQ(%) |
|---|---|---|---|---|---|
| 1 | 260 | 2.26 | 9.06 | 1.58 | 3.51 |
| 2 | 260 | 2.03 | 5.10 | 2.03 | 5.10 |
| 3 | 250 | 1.45 | 6.31 | 1.45 | 2.85 |
| 4 | 250 | 2.09 | 5.18 | 1.28 | 2.36 |
| 5 | 250 | 1.14 | 2.04 | 1.14 | 2.04 |
表1 4936个测试电感在2.5GHz下电感值和品质因数估计的最大相对误差
| N | 训练 | 在线验证 | CPU时间 | e L(%) | e Q(%) | e L(%) | e Q(%) |
|---|---|---|---|---|---|---|---|
| 广泛验证 | 广泛验证 | ||||||
| 1 | 123 | 88 | 0.94h | 0.27 | 1.25 | 0.28 | 0.91 |
| 2 | 253 | 177 | 10.03h | 0.20 | 0.74 | 0.21 | 0.66 |
| 3 | 207 | 150 | 11.30h | 0.22 | 1.01 | 0.22 | 0.69 |
| 4 | 197 | 145 | 18.81h | 0.22 | 0.99 | 0.21 | 0.55 |
| 5 | 140 | 102 | 20.23h | 0.22 | 0.88 | 0.19 | 0.46 |
表2 用于构建SLQ模型的样本数量
SLQ模型的电感值和品质因数平均相对误差(广泛验证)。
DOI10.1002/mop微波与光电子技术快报/第59卷,第5期,2017年5月 1209
S参数以及在整个设计空间中以所需精度对电感值和品质因数的 估计,本文所选择的电感值和品质因数估计中的相对误差阈值为
eL,eQ <6%对于电感值 [0.05,0.5]纳亨; eL,eQ <3%对于电感值>0.5纳亨。
其中eL 和eQ 分别是电感值L和品质因数Q的相对误差值。
所选择的阈值(3%)在精度和计算时间(新样本的电磁仿真) 之间实现了良好的权衡。对于L< 0.5nH的情况,考虑采用 更高的阈值以减少模型构建所需的电磁仿真次数,因为这些电感器在电路设计中很少使用。通过所提出的误差度量 方法计算得到的参数化宏模型(SLQ模型)能够更准确地建 模集成电感器的性能,从而有助于改善射频电路的设计,下一节将对此进行说明。
表1中的结果表明,在相同的Mabs误差阈值下,与相应 的模型S相比,S参数的精度有显著提升。此外,表2展示了在 一项广泛的验证研究中,针对4936个测试电感器的电感值L和 品质因数Q的平均相对误差( eL和eQ)。表2还包含了用于 构建参数化宏模型的(w,Din)样本总数,其中包括在自动建模 阶段用于验证模型精度的样本,以及对训练与验证所用电感器 进行仿真所需的CPU时间。
3. 电感综合与压控振荡器设计
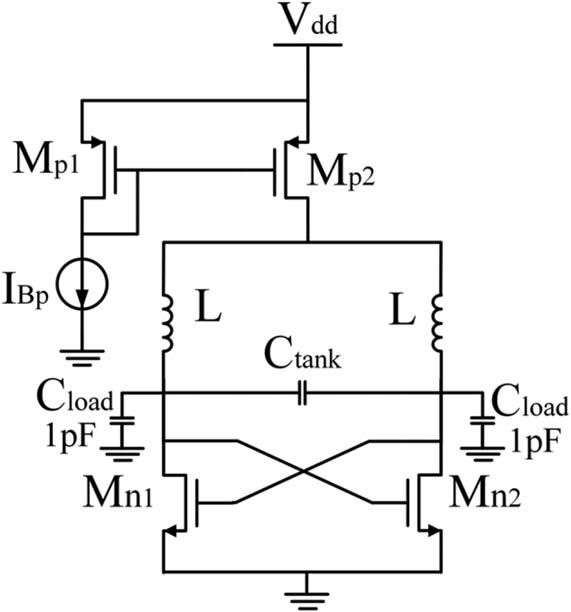
本节设计了一个单差分压控振荡器(如图3所示),以展示所 提出的建模策略(SLQ模型)相较于先前技术(模型S)以及 射频设计师使用的其他方法(例如电磁仿真)的优势。
在设计需要电感器的电路(例如压控振荡器)时,设计 人员通常寻找具有特定电感值和高品质因数的电感器(例如, 通过提高电感器的品质因数可降低压控振荡器相位噪声)。
为了获得最优电感,将使用三种不同的性能评估器进行优化: 电磁仿真器ADSMomentum、S模型和SLQ模型。随后将比 较优化结果和效率。所使用的优化算法为粒子群优化算法 (PSO[10])(包含40个个体和200代),目标是在最大面 积为165微米2的限制下,设计出电感值L=52±0.05nH且 品质因数最大的电感器。
然而,为了为射频电路正确设计电感器,必须应用一组高 度复杂的约束条件。
这些约束条件在以下方程组[7]中给出:
$$
\begin{cases}
\text{area} < 400\,\mu m \times 400\,\mu m \
\left|\frac{L @ WF - L @ (WF+0.05\,\text{GHz})}{L @ WF}\right| < 0.01 \
\left|\frac{L @ WF - L @ (WF-0.05\,\text{GHz})}{L @ WF}\right| < 0.01 \
\left|\frac{L @ WF - L @ 0.1\,\text{GHz}}{L @ WF}\right| < 0.05 \
Q @ (WF+0.05\,\text{GHz}) - Q @ WF > 0
\end{cases}
$$
(2)
其中L@W F 和Q@W F 是工作频率(WF)下的电感值和品质 因数,L @ W F 6 0.05 G Hz 和Q@W F 6 0.05 G Hz 是WF60.05GHz 下的电感值和品质因数。
这些约束条件用于确保电感值在从接近直流到略高于工 作频率的范围内足够平坦,电感器的自谐振频率远高于工作 频率,最后,因工艺变化引起的L和Q值偏差最小化[7]。这 些约束条件也是需要如此精确的L和Q值估计的另一个原因: 如果存在例如6%的误差(如模型S所得结果),则可能错误 地计算这些约束条件,导致优化结果落在实际未满足约束的 区域。
| N | Din (μm) | w (μm) | L@2.5 GHz | DL (%) | Q@2.5 GHz | DQ (%) | CPU time |
|---|---|---|---|---|---|---|---|
| EM | 3 | 111 | 7.25 | 1.99 | – | 10.32 | – |
| SLQ | 3 | 111 | 7.4 | 1.99 | 0.04 | 10.34 | 0.34 |
| S | 3 | 110 | 7.6 | 1.98 | 0.71 | 9.75 | 6.21 |
表3 使用三种不同性能评估器进行电感综合的结果
| 组件 | EM | SLQ | S |
|---|---|---|---|
| W n1,2(微米) | 75 | 75 | 75 |
| l n1,2(微米) | 0.35 | 0.35 | 0.35 |
| W p 1(微米) | 50 | 50 | 50 |
| W p 2(微米) | 150 | 150 | 150 |
| 电感值 p 1,2(微米) | 3 | 3 | 3 |
| I BP (mA) | 1 | 1 | 1 |
| C tank (fF) | 397 | 395 | 403 |
表4 压控振荡器仿真中使用的组件值
| 方法 | 相位噪声 dBc/Hz | D (%) | ƒ osc(吉赫) | D (%) | V out(V) | D (%) |
|---|---|---|---|---|---|---|
| EM | -124.11 | – | 2.50 | – | 1.01 | – |
| SLQ | -124.12 | 0.01 | 2.50 | 0.02 | 1.01 | 0.27 |
| S | -123.68 | 0.37 | 2.50 | 0.36 | 0.97 | 4.40 |
表5 使用已合成的电感的VCO性能
表3展示了使用不同性能评估器进行三次优化的结果。每次过程所需的CPU时间也在表3中给出。请注意,模型生成还需要表2中所示的CPU时间,但这只是一次性投入,生成的模型可以根据需要多次使用,因此构建模型所用的时间不应计入本次优化中。
所有技术都能实现类似的电感器,但模型S和SLQ比使用 电磁仿真的优化方法高效得多。采用模型S得到的电感器品质 因数低于其他方法,而采用SLQ模型和电磁仿真得到的电感 值更接近目标值(2纳亨)。
随后,通过电磁场仿真对模型得到的电感器进行了仿真, 以检查模型误差(参见表3中的DL和DQ列)。可以得出结论, 由于模型S的预测误差较高(Q值误差约为6%),使用模型 S的优化未能收敛到与SLQ模型相同的电感器。因此,在给定 应用中,使用模型S可能导致射频设计师选择次优电感器。
综合过程中获得的每个电感器随后被用于在0.35微米 CMOS工艺中设计不同的压控振荡器(VCO),其振荡频率 (ƒosc)为2.5GHz,电源电压为Vdd5 1.5V。
每个设计的压控振荡器(VCO)的设计变量如表4所示, 其中Wn1,2为差分对晶体管的栅极宽度,ln1,2为这些晶体管的 沟道长度,Wp1、Wp2为用于偏置电路的电流镜的栅极宽度, lp1、lp2为其沟道长度。最后,C1为VCO谐振槽中使用的电 容器。每种方法中使用的电感器均为综合设计所得(见表3)。
尽管Ctank的值需要在不同的压控振荡器之间进行调整 (以获得所需的ƒosc),但所有其他组件都固定为相同值,以 便考察不同得到的电感器对压控振荡器性能的影响。
所有电路仿真均使用CadenceSpectreRF电路仿真器 [11]完成。结果如表5所示。可以看出,当采用SLQ模型获得 的电感器时,VCO性能更优(相位噪声更低,输出电压更高), 这是因为在优化阶段SLQ模型获得了更高品质因数的电感器, 证明了该新建模策略在电路设计中带来的优势。
由模型得到的电感器存在一定的误差,如表3所示。因此, 对电感器进行了电磁仿真,并将其用于电路仿真,以比较使 用模型时VCO性能的偏差。偏差如表5所示,用D表示。可以 看出,对于所有VCO性能而言,SLQ模型提供了出色的精度 (优于模型S),相对于使用电磁仿真电感器获得的相应 VCO性能,其偏移可忽略不计。在另一方面
 压控振荡器相位噪声,(b) 压控振荡器瞬态仿真,以及(c) 压控振荡器输出电压频谱)
压控振荡器相位噪声,(b) 压控振荡器瞬态仿真,以及(c) 压控振荡器输出电压频谱)
另一方面,使用模型S综合的电感器所获得的VCO性能在输 出电压(Vout)上存在约5%的误差,而输出电压是一个关键 性能指标(VCO的输出电压会显著影响混频器的转换增益及 其线性度)。使用模型SLQ得到的VCO性能如图4所示,其 中描绘了相位噪声、瞬态仿真结果以及输出电压频谱。
4. 结论
本文提出了一种采用针对集成电感器建模而定制的顺序采样 方法构建的参数化宏模型。该新方法能够在不同的性能参数 上实现误差度量,并提高时域建模精度。已进行了广泛的验 证研究,证明了在L和Q值估计方面的模型精度优于仅基于S 参数误差度量的模型。当应用于射频电路设计中的综合方法 时,这种新的建模技术已证明其在提升性能方面的价值。此 外,在考虑自动化电路设计方法时,由于SLQ模型相较于传 统的电磁仿真具有更高的精度和效率,因此为获取电感器性 能估计提供了一种有效的方法。




















 375
375

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








