基于瞬发γ电流的钒探测器补偿

基于钒探测器补偿瞬发γ电流的机械shim应用研究

1. 引言

西屋公司（西屋电气有限责任公司，宾夕法尼亚州克兰伯里镇西屋大道1000号572A室，邮编16066）开发了一项先进技术，称为“机械补偿” （MSHIM），仅使用控制棒组件来控制反应堆功率和轴向功率偏移。该技术满足了电力公司需求文件中关于负荷跟踪运行而无需调节硼浓度的要求。该技术已（或将要）应用于系统 80þ（帕洛弗迪核电站，美国亚利桑那州西部托诺帕），第三代非能动安全反应堆（AP1000）以及小型模块化反应堆（IRIS）[1 e 3]。

由于无需通过调节硼浓度来适应变负荷和负荷调节运行，机械补偿 （MSHIM）通过控制控制棒组件的移动来实现调节，从而显著减少了放射性液体废物排放。然而，频繁移动控制棒的运行模式对基于校准堆外功率测量[4,5]的传统堆芯功率保护和轴向功率偏移控制方法产生了显著影响。通常，钒探测器用于提供非常精确的堆芯核功率分布。但钒探测器具有超过10分钟的延迟时间响应[6]，限制了其在轴向偏移控制中的直接应用。可采用滞后‐超前算法来补偿该延迟时间响应。

补偿，由此可将已补偿的信号用于调节瞬发、基于堆外功率的轴向偏移控制[7]。事实上，堆内钒探测器同时产生β 电流和瞬发γ 电流。由于钒探测器的瞬发γ 电流相对于β 电流较弱，通常被忽略。本文提出一种专用的超前‐滞后单元设计，用于补偿延迟的β 信号电流，并利用瞬发γ 电流以实现快速响应且稳态误差可忽略的设计。此外，通过MATLAB/Simulink数值模拟验证了该设计的性能。

2. 机械补偿的轴向偏移控制及其补偿

恒定的轴向偏移控制要求堆内核功率的上半部与下半部之和与其偏差保持恒定比例，因此功率的变化必然导致轴向偏移的变化。通常，上下半部的功率测量是通过堆外功率量程的顶部和底部探测器[1e3,8]获得的。在传统的第二代压水堆大多数运行条件下，控制棒几乎完全从活性堆芯区域抽出（全棒提出），且移动非常少，从而形成均匀的堆芯功率分布。然而，在机械补偿（MSHIM）策略中，控制棒组件的频繁移动破坏了堆外与堆内轴向偏移之间的一致性。控制棒组件的抽出会导致轴向偏移上倾，而插入则会引起轴向偏移下倾。此外，堆外探测器对外围区域面对的燃料组件较为敏感，加剧了堆外测量的轴向偏移与实际堆内轴向偏移之间的可能偏差。图 1[5]展示了基于堆外测量的轴向偏移（AOex）与基于外围燃料组件的轴向偏移（AOwp） 以及堆芯轴向偏移（AOin）之间的相关性。由于堆芯轴向偏移与堆外测量的轴向偏移之间存在显著偏差，保护系统采用基于堆外加权外围燃料组件的校准后的轴向偏移[4,5]。保护系统将校准信号传输给控制系统用于轴向偏移控制，这可能会限制反应堆功率或运行能力。

钒自给能中子探测器（SPNDs）具有的优势，例如更长的寿命、简单的响应特性以及更换后的自给能中子探测器易于处理，使其成为堆芯内通量分布映射应用的理想候选。例如，堆芯内均匀配置了42个自给能钒探测器组件，每个组件由七个纯化 51V组成，最长的探测器长度等于堆芯活性区长度，其余六个探测器的长度依次比最长的缩短七分之一[1电子3]。一个组件内钒探测器的位置如图 2[7]所示。

基于堆内钒探测器的电流与核功率具有良好的一致性，除了在堆芯中指定的布局外，位于j区域的探测器测量得到的堆芯上下半部功率偏差D∅表示如下：

$$ D∅ = PjT − PB = Kc_j \cdot (I_{4j} + I_{5j} − I_{1j}) $$
(1)

其中，Kc_j 表示位于 j 区域的 cth 探测器的因子，Icj 是从位于 j 区域的 cth 探测器输出的电流。

为了与保护系统的四个部分的四个功率偏差信号相关联，42个探测器组件被分为四个象限。IAPi表示第ith象限的功率偏差。

$$ IAP_i = m_{ai} \left( \frac{1}{N_i} \sum_{j=1}^{N} I_{4j} + \frac{1}{M_i} \sum_{j=1}^{M} I_{5j} − \frac{1}{P_i} \sum_{j=1}^{P} I_{1j} \right) + b_{ai} $$
(2)

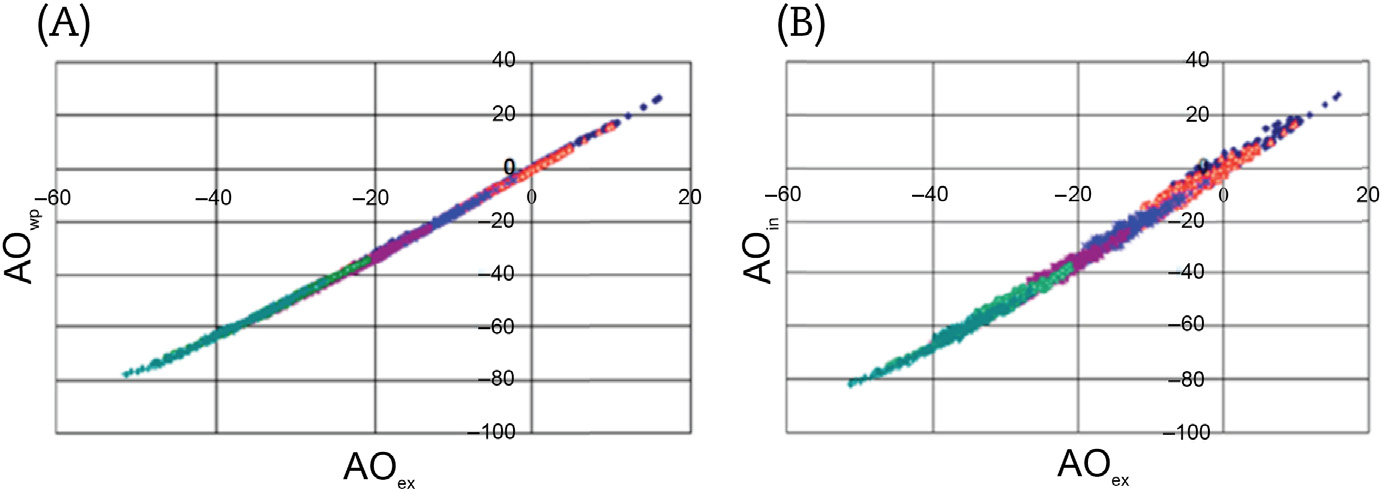
如图1所示，MSHIM运行模式导致基于外围燃料组件校准测量的 ðAFDWP_i Þ与堆芯轴向偏移之间存在显著不一致；同时，轴向偏移控制系统接收这些AFDWP_i用于轴向偏移控制。Xu [7]提出了一种调节AFDWP_i的方法，该方法采用带有幅值限制器的时间延迟已补偿IAPi。

$$ D_{ai}(t) = \frac{1}{N} \sum_{j=0}^{N} \left[ IAP_i(t−j) − AFDWP_i(t−j − τ) \right] $$
(3)

$$ AFD_i(t) =
\begin{cases}
AFDWP_i(t) + D_{ai}(t), & D_{ai}(t) − d_{ai}(t) < 0 \
AFDWP_i(t) + d_{ai}(t), & D_{ai}(t) − d_{ai}(t) ≥ 0
\end{cases} $$
(4)

其中，N 是为提高稳定性而在平均时间窗口内的计数数量，τ 是已补偿信号与堆外对应信号之间的时间差，dai(t) 是预定义的限幅器。仿真结果表明该方法具有良好的效率，但该方法的性能取决于时延补偿的特性以及 τ 的合理选择。

3. 钒探测器的时间延迟补偿

3.1. 钒探测器产生的电流

钒（51V）探测器具有结构简单、体积小、无需高压偏置、燃耗低以及典型的1/V中子响应特性，被广泛应用于核电站。钒探测器产生的电流由三种效应组成。当中子在钒发射体中被俘获时，形成一种俘获产物同位素，该同位素通过b发射 d衰变，其中99.2%的发射具有 2.5404兆电子伏特的终点能量[9]。通常情况下，42%的b发射能量足够高，能够逸出钒和绝缘体，产生与中子通量成正比的电流[10]。

上述钒中的中子俘获过程总是伴随着瞬发俘获g射线的发射。这些 g射线’的能量整体或部分通过相互作用被钒吸收，经由康普顿效应、光电效应过程和电子对产生释放出电子。部分电子能量足够高，能够逸出钒和绝缘体，从而产生电流。在20世纪80年代初，许多关于利用SPNDs中[11 e13] g信号的研究得以开展。由于裂变产物带来的伽马本底以及转换效率低，这部分产生的电流通常被忽略[14]。反应堆入射到探测器本身的g射线会产生康普顿电子、电子对以及光电子，其中一些电子能量足够高，可产生电流。尽管这种由入射g引起的电流是瞬发的，但在动力反应堆中大约有50%的该g流是延迟的，因此无法实时跟随通量变化。

因此[10,15],将这些g引起的电流视为干扰。图3展示了入射辐射（包括中子和g）转化为高能电子的三种主要机制。

通常，仅考虑由β相互作用产生的电流，因此

$$ I(t) = K \cdot sa \cdot e \cdot N \cdot \phi \cdot \left(1− e^{− 0.693t / T_{1/2}}\right) $$
(5)

其中，K、sa、e、N 和 ∅ 分别表示材料因子、热中子活化截面、电子因子、钒的原子数和热中子通量；T1/2 表示钒的半衰期。

如公式5所示，当t趋近于无穷大时（∞），探测器产生的电流与中子通量成正比。尽管 52V的半衰期为225秒，但由于探测器材料并非由100%纯钒制成，因此钒探测器在阶跃输入下的中子通量率响应时间常数为326秒’。换句话说，探测器输出电流在326秒内达到最终值的63%。探测器特性可用

$$ W_1(s) = \frac{1}{326s + 1} $$
(6)

其中 s 是拉普拉斯变换的变量。 图4 显示了阶跃通量变化下的时间响应。

3.2. 电流补偿方法简要回顾

如图4所示，钒探测器达到稳态（最终值的93%）输出所需的时间约为15分钟，这限制了其在核电站中的应用。通常，钒探测器用于堆芯通量分布计算。为了充分发挥探测器的优势，已开发出多种补偿算法。

典型的补偿算法包括逆函数[6],卡尔曼滤波[17], H∞滤波[18],基于计算机采样的软件[19],最新滤波[20,21]。超前‐滞后补偿器通常用于反馈控制系统中，以改善不良频率响应。合理配置的超前‐滞后单元可显著提升动态响应和抗噪声能力，因此已被应用于核电站的控制系统中。考虑到钒探测器相对简单的中子响应特性、这些算法的成本以及超前‐滞后单元的动态响应特性[22],在探测器后采用基于超前‐滞后的补偿单元

3.3. 优化补偿

正如李[15]指出的那样，尽管探测器的γ感应电流很小，但在特定条件下应通过热中子灵敏度校准予以消除。应给出一种用于γ和β感应电流流灵敏度识别的方法。瑞典KWD核仪器公司的产品规格表明，在 10¹⁴ n/cm²/s热中子通量率条件下，热中子β电流流为0.51 μA，而γ感应电流流为0.007 μA。因此，γ感应电流流占总电流流的1.4%。威廉[23]也指出，γ感应电流约占所产生的总电流流的1%。通常认为，约50%的γ感应能量由瞬发γ[8]产生；此外，由于转换效率低，探测器本身的(n, γ, e)效应可忽略不计。

因此，认为大约50%的γ感应电流是通过(γ, e)入射瞬发γ产生的，这同时反映了中子通量变化。以下设计的超前‐滞后补偿算法旨在利用这些有价值的动态电流信号。

考虑到瞬发γ电流占总电流流的K%，探测器的电流特征可表示为

$$ W_{1o}(s) = \frac{1}{326s + 1} $$

优化补偿单元 $ W_o(s) $ 设置为

$$ W_o(s) = \frac{(326s + 1)(100 - K)}{3.26K(100 - K)s + 100} $$
(8)

因此，系统的总体传递函数为

$$ Y(s) = \frac{K}{100} + \frac{1}{326s + 1} \cdot \frac{(326s + 1)(100 - K)}{3.26K(100 - K)s + 100} $$
(9)

当堆芯内输入为单位阶跃通量变化时，有 $ Y(\infty) = 1 $：基于时域和频域的镜像特性，时域中的输出为

$$ y(0^+) = 1 $$
(10)

同样，$ Y(0) = 1 - K^2/10000 $，表示时域中的输出

$$ y(\infty) = 1 - \frac{K^2}{10000} $$
(11)

通常情况下，K 非常小，则 $ y(\infty) \approx 1 $。

4. 仿真与分析

所有以下示例均使用MATLAB/Simulink进行计算，以验证所提方法的性能。

在无补偿、使用 $ W_2(s) = \frac{326s+1}{s+1} $ 进行已补偿，以及使用前述优化方法并采用 $ W_o(s) = \frac{(326s+1)(100-K)}{3.26K(100-K)s + 100} $（其中K = 0.6）的情况下，对单位阶跃激励的输出如图4所示。

仿真表明，利用瞬发γ电流信号的优化补偿在动态响应方面相较于之前的补偿具有巨大优势。

假设输入具有随机特性，即单位阶跃变化、负向单位阶跃变化和无变化的概率相同，则无补偿、有补偿以及优化补偿情况下的整体输出如图5A所示。部分仿真结果的放大细节如图5B所示。

图5 显示，没有进行任何补偿的原始系统具有强烈的低通滤波特性，无法很好地跟随输入信号；因此，高频信号的损失过大而难以接受。然而，经过补偿的方法响应要好得多，尽管存在一些超调。采用优化补偿的系统响应能非常好地跟随输入信号，在动态和稳态特性方面均显著优于其他方法。

图6 显示了不同K值之间的微小差异，即分别为0.3、0.6和0.9，这表明该方法具有广泛的适用性。

如图7所示，在两种极限情况下使用错误参数进行补偿时，响应并未退化到不可接受的水平，这表明优化补偿方法具有参数（K）鲁棒性。

图8A 显示输入在前端（即堆芯内）受到噪声污染的情况。图8B 显示电噪声在后段产生的情况，即在将电流传输至信号处理设备的电缆中产生的电噪声。由于具有较大的用于探测器的低通滤波器时间常数，前端感应噪声对输出影响很小。

图8B 表明后端感应噪声显著降低了参考补偿和优化补偿两种方法的性能。在这两种情况下，后者相较于前者具有更优的性能，因其能更紧密地跟随输入信号。对于 AP1000，与探测器直接连接的信号处理设备安装在安全壳内，并且非常靠近包含所有探测器的反应堆压力容器。从探测器到设备的专用电缆进一步最小化了潜在的信号污染[1电子3]。

需要注意的是，公式(5)具有近似精度。与温度相关的绝缘电阻会影响来自探测器的实际电流。Yu [14], Yang 等人[16],以及 Moreira 和 Lescano [24]的研究表明，温度会影响钒探测器的测量电流。Rao 和 Misra [25]指出，钒探测器的中子灵敏度应考虑其他因素，即探测器引起的通量凹陷和伽马射线的相互作用，这两种因素对应的修正因子分别被评估为 0.957 和 1.03。事实上，通常堆芯内探测器的温度以及温度测量变化较慢。从工程角度来看，对探测器进行时间上的校准可以考虑上述所有因素，从而实现预期的精度。同时，不同制造商的探测器时间常数可能会略有差异。如有需要，可对其进行论证并替换本文所采用的 326秒 时间常数。

5. 结论

结合超前‐滞后动态补偿特性以及通常被忽略的钒探测器瞬发γ电流流动特征，提出了一种基于实际瞬发γ探测器电流占比的超前‐滞后补偿器配置方法。数值模拟表明，该方法在阶跃和随机激励输入下可显著改善探测器的动态响应。

由于这种优化补偿具有更快的时间响应，并结合[7]在MSHIM模式下调节轴向偏移控制的方法，可预期整体系统性能将大幅提升，且可直接将τ在公式(3)中设为零。该方法还提供了仅使用已补偿的钒探测器电流信号进行轴向偏移控制的可能性。探测器的占比鲁棒性表明该方法具有显著的工程优势。如何方便地获取单个探测器的占比比例以实现最佳性能，是后续研究的关键重点。