无权图的单源最短路径

就像日常生活中的搭地铁问题，有的人会选择到达目的地最短距离的路线，有的人会选择地铁换乘次数最少的路线，其目的都是为了尽快到达目的地。选择到达目的地距离最短的路线，可以把两结点边的权值看成距离，而选择换乘次数最少的路线，可以把边的权值看作时间（换成次数少不代表路线就短嘛）。

图论中的最短路径问题，一般指一个无向图（或有向图），边的权值理解为两结点的距离，最短路径就是在求两个不同顶点的所有路径中，边的权值之和最小的那条路径。

而单源最短路径，是指从一个源点出发，到其他顶点的最短路径问题。在求单源最短路径时，我们遵守一个算法，由迪杰斯特拉提出的：“按路径长度递增的次序产生最短路径的算法”。

举个例子：

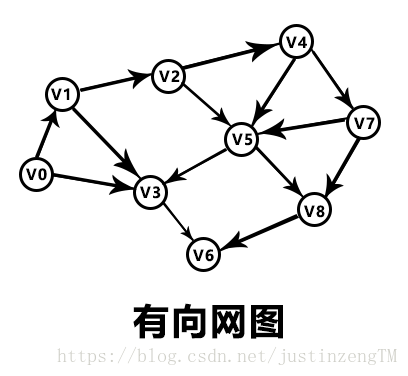
图中从路径长度为0开始，也就是VO源点本身。接下来寻找路径长度为1的路径，V1和V3，V1和V3是V0的直接邻接点。路径长度为2的邻接点就是V2和V6，路径长度为3的是V4和V5，路径长度为4的是V7和V8，最后路径长度为5的是V6，到这一步后，图中所有的顶点都被访问过了，所以算法到这就结束了。

0：V0；

1：V1和V3；

2：V2和V6；

3：V4和V5；

4：V7和V8；

5：V6；