参数高效微调三剑客：LoRA、MoLoRA与MoR1E的深度比较与应用指南

架构进化论

已于 2025-06-28 09:14:37 修改

阅读量842

点赞数 11

CC 4.0 BY-SA版权

分类专栏：大模型文章标签：人工智能深度学习大模型 LLM 机器学习

于 2025-06-27 12:45:00 首次发布

本文链接：https://blog.youkuaiyun.com/jsntghf/article/details/148770097

大模型专栏收录该内容

73 篇文章

订阅专栏

大模型微调的技术演进

在大型语言模型(LLM)时代，全参数微调(Full Fine-tuning)面临三大挑战：

计算资源消耗：微调百亿参数模型需昂贵GPU集群
存储开销：每个下游任务需保存完整模型副本
灾难性遗忘：微调可能损害模型原有通用能力

生活案例：想象一位精通多国语言的翻译专家(预训练模型)。传统微调如同让他完全转行(如从翻译转为医学诊断)，不仅需要大量培训(计算资源)，还可能丢失原有语言技能(灾难性遗忘)。而PEFT方法则像配备专业术语手册(适配器)，在保持核心能力的同时快速适应新领域。

技术全景图与核心思想

LoRA：低秩适应的开创者

核心思想：将权重更新ΔW分解为低秩矩阵乘积：

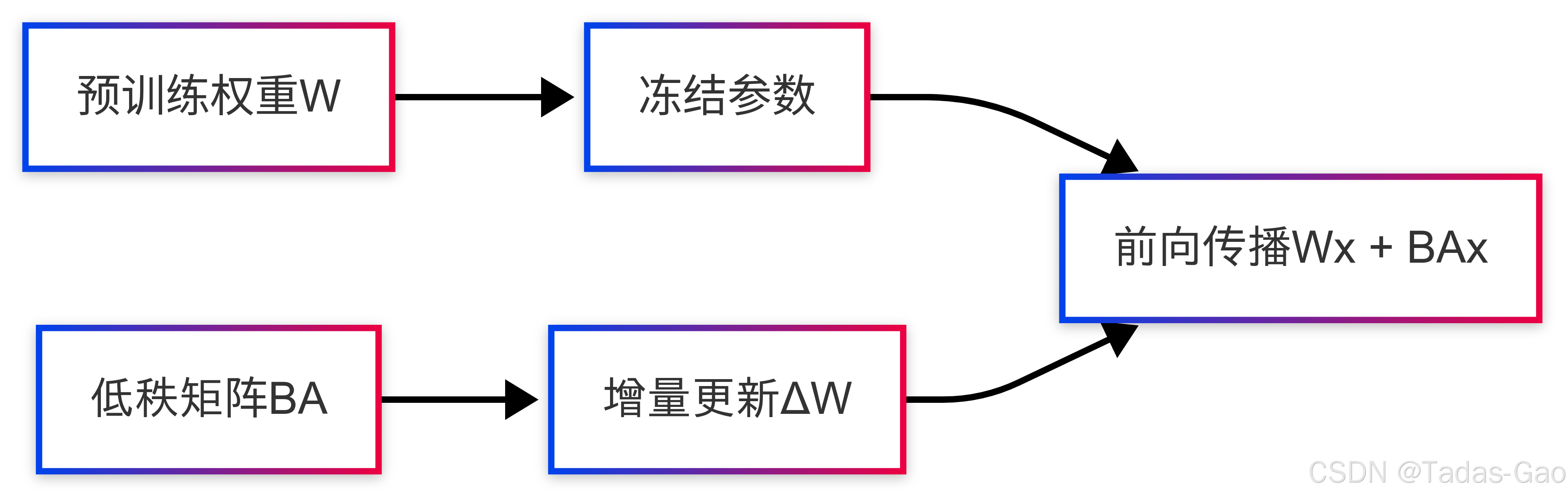
$\Delta W = BA \quad \text \quad B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times k}, r \ll \min(d,k)$

代码实现：

class LoRALayer(nn.Module):
    def __init__(self, d_model, r=8):
        super().__init__()
        self.A = nn.Parameter(torch.randn(d_model, r))  # 低秩矩阵A
        self.B = nn.Parameter(torch.zeros(r, d_model))  # 初始为0的矩阵B
        
    def forward(self, x):
        return x @ self.A @ self.B  # 低秩变换

优点：

参数效率极高(仅需0.1%-1%参数量)
零推理延迟(可与原权重合并)
广泛兼容各类模型架构

缺点：

低秩假设限制模型表达能力
静态适配无法应对输入多样性
在持续预训练等任务上表现欠佳

适用场景：资源受限环境下的轻量微调，如移动端部署、多任务快速适配。

MoLoRA：混合专家的动态适配

核心思想：集成多个LoRA专家并动态路由：

$y = \sum_{i=1}^n G(x)_i \cdot \text{LoRA}_i(x)$

其中 $G(x)$ 为门控网络。

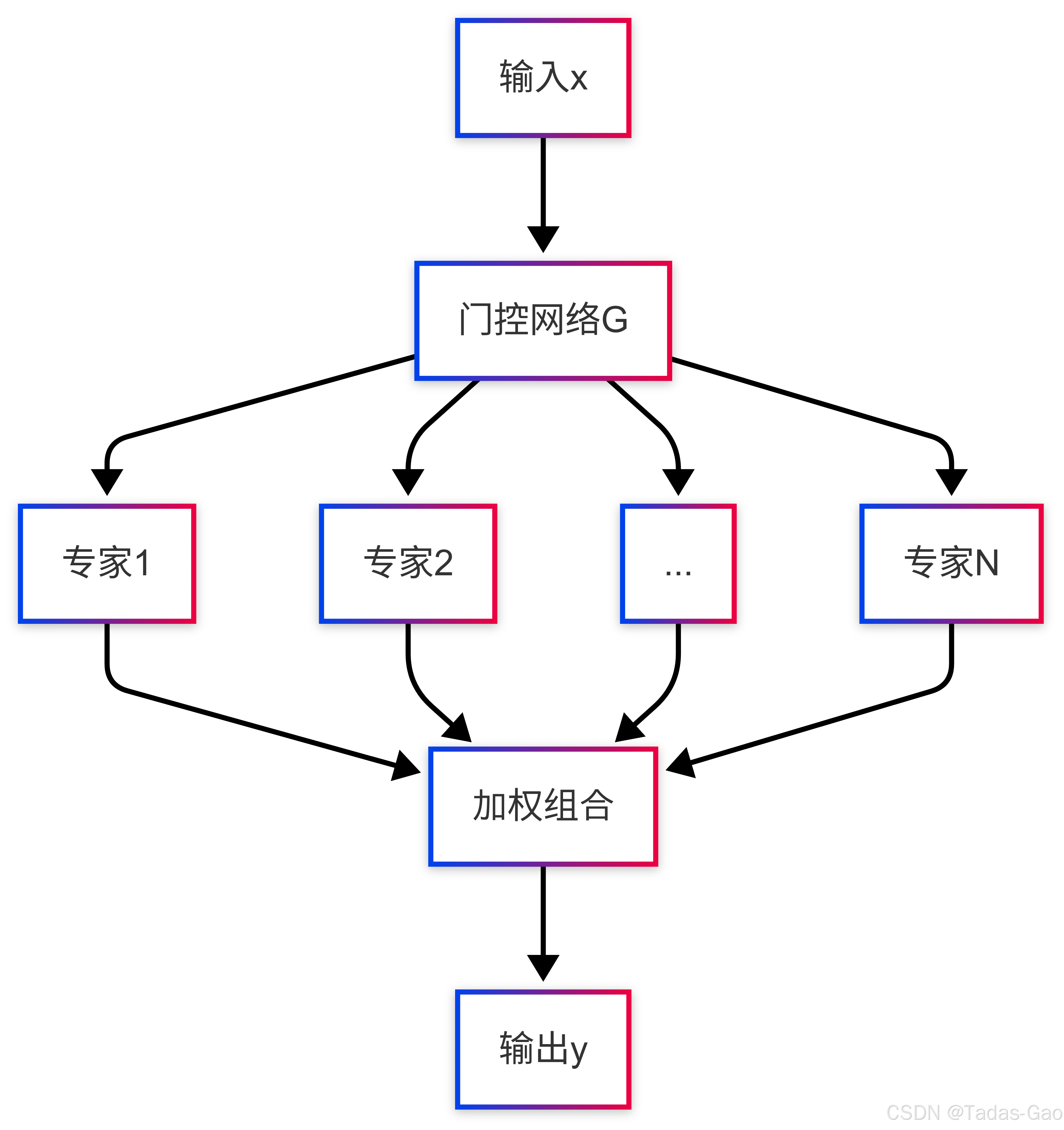
代码实现：

class MoLoRALayer(nn.Module):
    def __init__(self, d_model, num_experts=4, r=8):
        super().__init__()
        self.experts = nn.ModuleList([LoRALayer(d_model, r) for _ in range(num_experts)])
        self.gate = nn.Linear(d_model, num_experts)  # 简单门控
        
    def forward(self, x):
        gate_scores = F.softmax(self.gate(x), dim=-1)
        expert_outputs = torch.stack([e(x) for e in self.experts], dim=1)
        return torch.einsum('be,be...->b...', gate_scores, expert_outputs)

优点：

相比LoRA性能提升7.4%
专家可扩展性强(参数增长慢)
缓解灾难性遗忘(专家分组)

缺点：

门控网络引入额外计算
专家负载均衡挑战
超参数(专家数)敏感

适用场景：复杂多领域任务(如医疗诊断)、需要平衡新旧知识的场景。

MoR1E：认知自适应的新范式

核心思想：直觉感知的rank-1专家混合：

$E_i(x) = u_i v_i^T x \quad \quad u_i,v_i \in \mathbb{R}^d$

门控机制：

$G(x) = \text{Softmax}(W_g \cdot \text{IntuitionExtractor}(x))$

代码实现：

class MoR1EExpert(nn.Module):
    def __init__(self, d_model):
        super().__init__()
        self.u = nn.Parameter(torch.randn(d_model))  # rank-1向量
        self.v = nn.Parameter(torch.randn(d_model))
        
    def forward(self, x):
        return torch.outer(self.u, x @ self.v)  # 外积实现rank-1变换

class MoR1ELayer(nn.Module):
    def __init__(self, d_model, num_experts=4):
        super().__init__()
        self.experts = nn.ModuleList([MoR1EExpert(d_model) for _ in range(num_experts)])
        self.gate = nn.Sequential(
            nn.Linear(d_model, d_model//8),  # 直觉提取器
            nn.Linear(d_model//8, num_experts)
        )
        
    def forward(self, x):
        gate_scores = F.softmax(self.gate(x.mean(dim=1)), dim=-1)  # 全局特征门控
        expert_outputs = torch.stack([e(x) for e in self.experts], dim=1)
        return torch.einsum('be,bhe->bh', gate_scores, expert_outputs)

优点：

参数效率极高(rank-1结构)
直觉感知的动态适配
在数学推理等任务表现突出

缺点：

专家间正交性难以保证
对门控网络设计敏感
小规模数据易过拟合

适用场景：需要精细领域适应的场景(如金融量化分析)、资源极度受限的边缘设备（扩展阅读：认知自适应混合专家模型：MoR1E的创新与演进-优快云博客、解剖MoR1E：认知自适应混合专家模型的底层原理与内核设计-优快云博客）。

技术对比与选型指南

三维度对比分析

指标	LoRA	MoLoRA	MoR1E
参数量	$O(d \times r)$	$O(n \times d \times r)$	$O(n \times d)$
计算开销	最低	中等	较低
表达能力	有限(低秩)	强(专家混合)	中等(rank-1)
动态适应	无	门控选择	直觉感知
最佳场景	通用轻量微调	多领域复杂任务	精细领域适应

典型应用场景

案例1 - 医疗影像诊断：

挑战：多模态数据(CT、MRI)、常缺失部分模态
方案：MoLoRA配合模态感知门控，不同专家处理不同模态组合
优势：参数效率(仅1.6%可训练参数)与鲁棒性兼备

案例2 - 移动端个性化推荐：

挑战：设备资源有限，需快速适配用户偏好
方案：MoR1E+知识蒸馏，rank-1专家捕获用户画像
优势：200KB级模型大小实现个性化服务

案例3 - 多语言翻译系统：

挑战：维护50+语言对，避免语言间干扰
方案：LoRA模块化设计，各语言对独立适配器
优势：快速部署新语言(仅需新增LoRA模块)

实现最佳实践

超参数调优建议

秩选择：

LoRA：代码任务建议r=16-64，数学任务r=8-32
MoLoRA：专家数4-8，各专家r=4-8
MoR1E：专家数通常4-6

训练技巧：

# 通用训练配置
optimizer = AdamW(lora_params, lr=1e-4)  # LoRA需更大学习率
scheduler = get_linear_schedule_with_warmup(optimizer, warmup_steps=500)

# MoLoRA负载均衡损失
def load_balancing_loss(gate_scores):
    prob = gate_scores.mean(dim=0)
    return (prob * torch.log(prob)).sum()  # 熵最大化

架构改进方向

分层专家分配：

高层网络分配更多专家(MoLA方案)

# 沙漏型专家分布：两头多中间少
expert_distribution = [8, 2, 2, 8]  # 对应4个层级

动态秩调整：

$r(x) = \sigma(W_r \cdot \text{MLP}(x)) \cdot r_{\max}$

根据输入复杂度动态调整秩大小。

未来展望

稀疏专家系统：结合Top-K路由降低计算开销
跨模态泛化：视觉-语言统一适配框架
量子化集成：1-bit专家降低部署成本

“未来的PEFT技术将像人类的自适应学习系统一样，在保持核心能力的同时，通过轻量级模块实现快速领域适应。”—— 引自MoR1E研究者

附录：完整代码示例

"""
完整的MoR1E实现示例
包含：直觉感知门控、rank-1专家、负载均衡
"""
import torch
import torch.nn as nn
import torch.nn.functional as F

class IntuitionExtractor(nn.Module):
    """轻量级直觉特征提取器"""
    def __init__(self, d_model, reduction=8):
        super().__init__()
        self.mlp = nn.Sequential(
            nn.Linear(d_model, d_model//reduction),
            nn.GELU(),
            nn.LayerNorm(d_model//reduction),
            nn.Linear(d_model//reduction, d_model//reduction)
        )
        
    def forward(self, x):
        # 提取全局特征：均值池化+MLP
        return self.mlp(x.mean(dim=1))

class MoR1E(nn.Module):
    """完整MoR1E层实现"""
    def __init__(self, d_model, num_experts=4):
        super().__init__()
        self.experts = nn.ModuleList([
            nn.ParameterList([
                nn.Parameter(torch.randn(d_model)),  # u_i
                nn.Parameter(torch.randn(d_model))   # v_i
            ]) for _ in range(num_experts)
        ])
        self.gate = IntuitionExtractor(d_model)
        self.gate_proj = nn.Linear(d_model//8, num_experts)
        
    def forward(self, x):
        # 计算门控权重
        gate_logits = self.gate_proj(self.gate(x))
        gate_weights = F.softmax(gate_logits, dim=-1)  # [B, num_experts]
        
        # 计算各专家输出
        outputs = []
        for u, v in self.experts:
            outputs.append(torch.outer(u, x @ v))  # [B, d, d]
        outputs = torch.stack(outputs, dim=1)  # [B, num_experts, d, d]
        
        # 加权组合
        return torch.einsum('be,becd->bcd', gate_weights, outputs)

通过本文的系统性分析，我们揭示了LoRA家族技术的演进脉络与设计哲学。在实际应用中，建议从任务复杂度、资源约束和性能需求三个维度进行技术选型，同时关注新兴的MoRA等高阶适配方案的发展。参数高效微调技术的精妙之处，恰在于用最少的参数变化激发最大的模型潜能——这或许正是AI工程与艺术的最佳结合点。