BSGS，扩展BSGS（求离散对数 b^x%p=n）

最新推荐文章于 2021-06-25 12:37:59 发布

JK Chen

最新推荐文章于 2021-06-25 12:37:59 发布

阅读量661

点赞数

CC 4.0 BY-SA版权

分类专栏：数论/数学知识点 ACM中的数学问题合集 All

本文链接：https://blog.youkuaiyun.com/jk_chen_acmer/article/details/99881255

All 同时被 3 个专栏收录

629 篇文章

订阅专栏

数论/数学知识点

48 篇文章

订阅专栏

ACM中的数学问题合集

44 篇文章

订阅专栏

本文深入讲解了大步小步法（Baby-Step-Giant-Step，简称BSGS）算法，这是一种在O(logP)时间内求解离散对数问题的有效方法。文章详细介绍了算法的过程，包括如何分解指数表达式，利用哈希链表优化查找效率，以及如何处理底数与模数不互质的情况。通过两个例题，展示了算法的具体应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

BSGS

大步小步法（ $B a b y - S t e p - G i a n t - S t e p$ ，简称 $B S G S$ ），可以在 $O (l o g P)$ 的时间内求出 $basex≡n(mod P)base^x\equiv n(mod\;P)$ 的解 $x$ ，也就是在模 $P$ 意义下，以 $b a s e$ 为底， $n$ 的离散对数。

其中要求 $(b a s e, P) = 1$ 。

过程

其实就是一个暴力而已，假定已知 $m$ ，将 $x$ 分解成 $b m - a$ 的形式，有： $basebm≡n∗basea(mod P)base^{bm}\equiv n*base^{a}(mod\;P)$
我们枚举 $a∈[0,m−1]a\in[0,m-1]$ ，将 $n*base^{a}\%P$ 打标记。然后再枚举 $b∈[1,P/m]b\in[1,P/m]$ ，判断 $base^{bm}\%P$ 是否被打标记，如果是，则说明找到了一对 $< a, b >$ ，带入得 $b m - a$ 就是答案。

显然，当 $m$ 取 $P\sqrt P$ 时 $a, b$ 的枚举次数期望最少。此时有 $b∈[1,m+1]b\in[1,m+1]$ 。

判断标记最好使用哈希链表，不然时间复杂度堪忧。

例题

original link - http://poj.org/problem?id=2417

/*
 *  Author : Jk_Chen
 *    Date : 2019-08-20-19.42.31
 */
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
using namespace std;
#define LL long long
#define rep(i,a,b) for(int i=(int)(a);i<=(int)(b);i++)
#define per(i,a,b) for(int i=(int)(a);i>=(int)(b);i--)
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define pill pair<int, int>
#define fi first
#define se second
const LL mod=1e9+7;
const int maxn=1e5+9;
LL rd(){ LL ans=0; char last=' ',ch=getchar();
    while(!(ch>='0' && ch<='9'))last=ch,ch=getchar();
    while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans; return ans;
}
/*_________________________________________________________head*/

LL Pow(LL a,LL b,LL mod){
    LL res=1;
    while(b>0){
        if(b&1)res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}

namespace Hash{
	const int Mod=102023;
	int head[Mod],nex[Mod],now;
	pill val[Mod];
	void init(){
	    now=0;
	    mmm(head,0);
	}
	void insert(int x,int y){
	    int key=x%Mod;
	    nex[++now]=head[key];head[key]=now;
	    val[now].fi=x,val[now].se=y;
	}
	int find(int x){
	    int key=x%Mod;
	    for(int i=head[key];i;i=nex[i]){
	        if(val[i].fi==x)return val[i].se;
	    }
	    return -1;
	}
}

void BSGS(int base,int n,int p){ // Pow(base, b*m) = n * Pow(base, a)
    if(n==1){
        printf("0\n");return;
    }
    Hash::init();
    // x = a + bm
    int m=sqrt(p);
    int tmp=n;
    rep(a,0,m-1){
        Hash::insert(tmp,a);
        tmp=1ll*tmp*base%p;
    }

    tmp=1;
    LL mul=Pow(base,m,p);
    rep(b,1,m+1){
        tmp=1ll*tmp*mul%p;
        int a=Hash::find(tmp);
        if(~a){
            printf("%d\n",b*m-a);
            return;
        }
    }
    printf("no solution\n");
}

int main(){
    int base,n,p;
    while(cin>>p>>base>>n){
        BSGS(base,n,p);
    }
    return 0;
}

同余定理

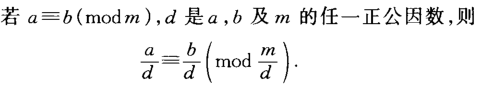
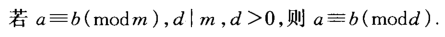
在这里插入图片描述

Extended BSGS

$B S G S$ 仅适用于 $(b a s e, P) = 1$ 的情况，对于非互质情况，需要用扩展算法进行转化。

我们提取 $d = (b a s e, P)$ ，原式 $basex≡n(mod P)→base^x\equiv n(mod\;P)\to$ $basex−1∗based≡nd(mod Pd)base^{x-1}*\dfrac{base}{d}\equiv \dfrac{n}{d}(mod\;\dfrac{P}{d})$
这里的 $(n,d)≠d(n,d)=\not d$ 时，根据同余定理可判断方程无解。

继续上述过程直至 $(b a s e, P) = 1$ ，有： $basex−k∗based1..dk≡nd1..dk(mod Pd1..dk)base^{x-k}*\dfrac{base}{d_1..d_k}\equiv \dfrac{n}{d_1..d_k}(mod\;\dfrac{P}{d_1..d_k})$
因为模数底数互质，所以可以直接对此式进行 $B S G S$ 。 $basebm−a∗based1..dk≡nd1..dk(mod Pd1..dk)base^{bm-a}*\dfrac{base}{d_1..d_k}\equiv \dfrac{n}{d_1..d_k}(mod\;\dfrac{P}{d_1..d_k})$ $basebm∗based1..dk≡nd1..dk∗basea(mod Pd1..dk)base^{bm}*\dfrac{base}{d_1..d_k}\equiv \dfrac{n}{d_1..d_k}*base^{a}(mod\;\dfrac{P}{d_1..d_k})$

最后的答案为 $b m - a + k$ 。

例题

original link - http://poj.org/problem?id=3243

/*
 *  Author : Jk_Chen
 *    Date : 2019-08-21-09.12.01
 */
#include<iostream>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<stdio.h>
using namespace std;
#define LL long long
#define rep(i,a,b) for(int i=(int)(a);i<=(int)(b);i++)
#define per(i,a,b) for(int i=(int)(a);i>=(int)(b);i--)
#define mmm(a,b) memset(a,b,sizeof(a))
#define pb push_back
#define pill pair<int, int>
#define fi first
#define se second
const LL mod=1e9+7;
const int maxn=1e5+9;
LL rd(){ LL ans=0; char last=' ',ch=getchar();
    while(!(ch>='0' && ch<='9'))last=ch,ch=getchar();
    while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans; return ans;
}
/*_________________________________________________________head*/

LL Pow(LL a,LL b,LL mod){
    LL res=1;
    while(b>0){
        if(b&1)res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}

namespace Hash{
	const int Mod=102023;
	int head[Mod],nex[Mod],now;
	pill val[Mod];
	void init(){
	    now=0;
	    mmm(head,0);
	}
	void insert(int x,int y){
	    int key=x%Mod;
	    nex[++now]=head[key];head[key]=now;
	    val[now].fi=x,val[now].se=y;
	}
	int find(int x){
	    int key=x%Mod;
	    for(int i=head[key];i;i=nex[i]){
	        if(val[i].fi==x)return val[i].se;
	    }
	    return -1;
	}
}

int BSGS(int base,int n,int p){ // Pow(base, b*m) * bd = n * Pow(base, a)
    if(n==1){
        return 0;
    }
    int d=__gcd(base,p);
    int bd=1,k=0;
    while(d>1){
        if(n%d){
            return -1;
        }
        n/=d;
        p/=d;
        k++;
        bd=1ll*bd*(base/d)%p;
        if(bd==n){
            return k;
        }
        d=__gcd(base,p);
    }

    Hash::init();
    int m=sqrt(p);
    int tmp=n;
    rep(a,0,m-1){
        Hash::insert(tmp,a);
        tmp=1ll*tmp*base%p;
    }

    tmp=bd;
    LL mul=Pow(base,m,p);
    rep(b,1,m+1){
        tmp=1ll*tmp*mul%p;
        int a=Hash::find(tmp);
        if(~a){
            return b*m+k-a;
        }
    }
    return -1;
}

int main(){
    int base,n,p;
    while(cin>>base>>p>>n,base|p|n){
        int res=BSGS(base,n,p);
        if(~res)cout<<res<<endl;
        else puts("No Solution");
    }
    return 0;
}