Burnside引理 & Polya计数

->置换群概念

为什么要分开呢？因为我觉得这块比较难理解，放在一起会“劝退”的
！！！一定要搞清楚上一部分的各种定义和符号

例题 例题

Burnside引理：

置换群G作用下等价类个数，等于每个置换$\pi$的不动点个数的平均数。

当然不动点类其实是有一个公式的（$Z_i$表示元素$i$的不动置换类，$C(\pi)$表示置换$\pi$的不动点集）

$$\sum_{i=1}^{n}Z_i=\sum_{\pi=1}^{|G|}C(\pi)$$

因为其实是两个两两对应的东西，所以应该很好理解

所以Burnside引理得出：

等价类个数 $L=\dfrac{1}{|G|}\sum_{i=1}^{n}Z_i=\dfrac{1}{|G|}\sum_{\pi=1}^{|G|}C(\pi)$

举个例子： $\\$ 经典的着色，有2*2的格子，每个1*1可以选择涂或不涂，且格子可以顺时针旋转，求方案数 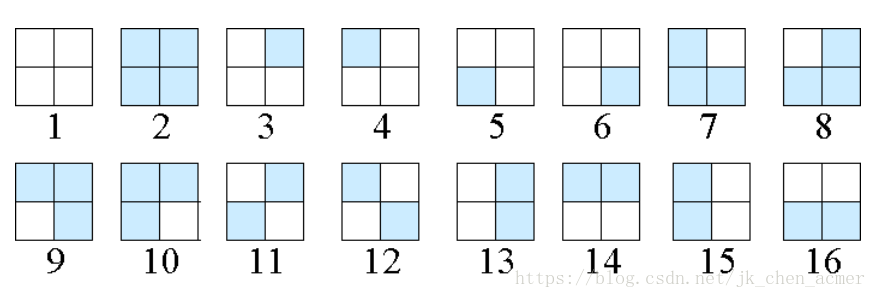着是所有可能的情况，将每种情况看成元素集X中的元素，而顺时针旋转$0^。,90^。180^。270^。$作为置换群G中的元素 $\\$ $\;0^。\;$：$(1)(2)…(16)；$ $90^。$：$(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)$ $180^。$：$(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12)(13 15)(14 16)；$ $270^。$：$(1)(2)(3 4 5 6)(7 8 9 10)(11 12)(13 14 15 16 )；$ $\\$ 那么$L=\frac{16+2+4+2}{4}=6$

从这个例子可以看出，等价类内的元素属于重复情况，Burnside引理可以在存在置换情况时，计算出实际的方案数。

$\\$

---

$\\$

Polya定理：

$c(\pi)$为置换$\pi$的循环节（未涂色，单纯以元素编号为对象）个数，polya定理用$m^{c(\pi)}$代替了$C(\pi)$。

定理内容：用m种颜色对置换群G（操作对象群X）涂色，等价类的公式公式如下：

$$L=\dfrac{1}{|G|}\sum_{\pi=1}^{|G|}m^{c(\pi)}$$

Polya定理相当于用一个较为容易得到的东西 , 替换了Burnside引理所需的不定点的个数，因为求循环节不需要列出所有的情况，只需要统计每种置换就可以得出答案

举个例子： $\\$ 还是这个问题 现在要求的不是每个置换的不动点数 , 而是每个置换的循环数。 $\\$ 注意polya定理的G的元是单个元素（相较于Burnside引理，其G中元为涂色结果的整体，也就是说Burnside引理是上面16种情况而polya定理是4个独立方块） $\\$ $\;0^。\;$：$(1)(2)(3)(4)；$ $90^。$：$(4,1,2,3)；$ $180^。$：$(1,3)(2,4)；$ $270^。$：$(2,3,4,1)；$ $\\$ 那么$L=\frac{2^4+2^1+2^2+2^1}{4}=6$

有没有感觉比上面枚举要简单很多呢
$\\$

---

$\\$

重点强调：

–Polya定理中的群G是作用在n个对象上的置换群
–Burnside引理中的群G是对这n个对象染色后的方案集合上的置换群

再写一遍，polya定理的G中元是单个元素，而Burnside引理的G中元为涂色结果的整体，也就是说Burnside引理是上面16种情况而polya定理是4个独立方块）。

$\\$

---

$\\$

环形polya：

用K种颜色涂色，当置换群是对一个长为N环的旋转M个位置的操作，有如下结论：循环个数为$gcd(N,M)$，那么根据polya定理，此时有：

$$L=\frac{1}{n}\sum_{i=0}^{n-1}K^{gcd(n,i)}$$

一般来说，你是不能枚举i的，要针对gcd进行优化，处理出有多少个i使gcd=x

$\\$

---

$\\$

Polya裸体：hdu 4633

有一个类似魔方的正方体，每面9个格子可涂不同颜色，而8个点和12条边也都涂色，正方体可以任意旋转，现有颜色K种，求方案数（两种正方体同构属于一种方案）

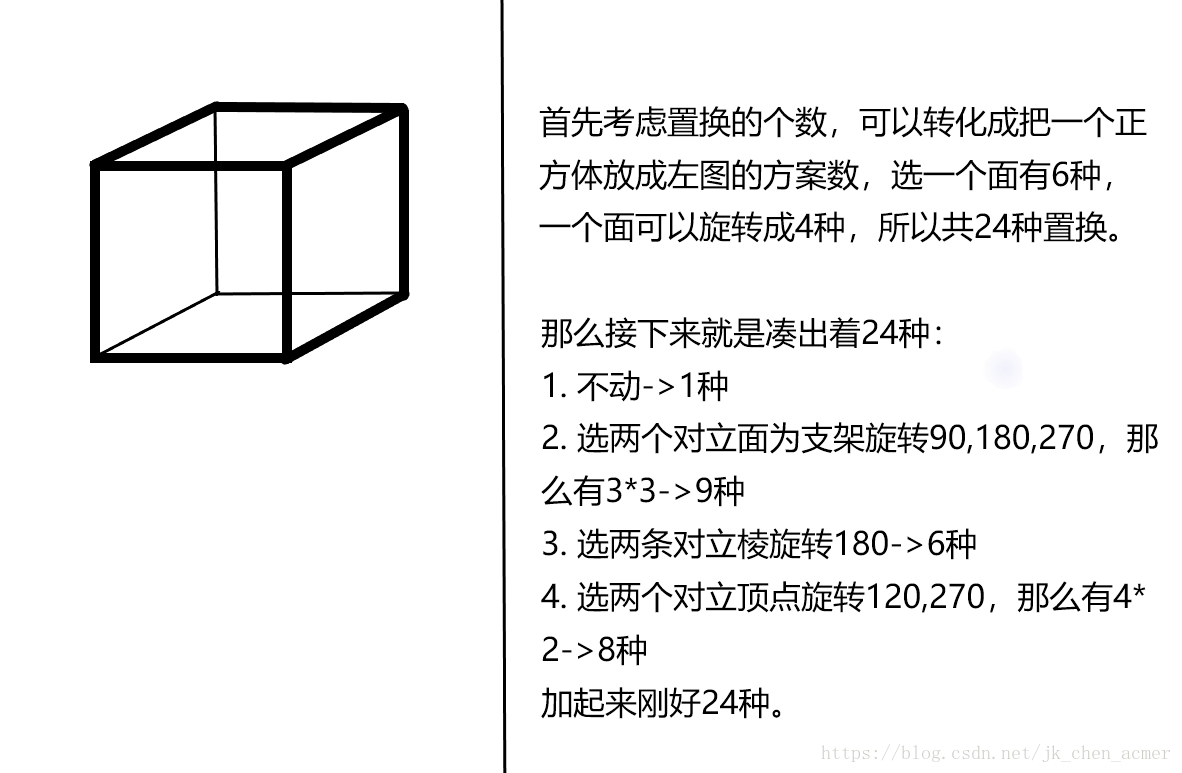
接下来根据polya定理，逐个分析每个置换的循环节数量

话说这部分如果空间想象力不好真的会比较难，你可以通过画图来帮助寻找哪些块在循环交换

• 不动：点8+面54+边12=74
• 按面旋转：（3对）
  
  • 90：点2+面15（上下左右四面对应->9+前后(1379)(2468)(5)->3*2）+边3=20
  • 180：点4+面28（上下对应->9+左右对应->9+前后(19)(28)(37)(46)(5)->5*2）+边6=38
  • 270：同90=20
• 按边旋转：（6对）
  
  • 180：点4+面27（上下对应->9+左右对应->9+前后对应->9）+边7=38
• 按顶点旋转：（4对）
  
  • 120：点4+面18（正左下对应->9+后右上对应->9）+边4=26
  • 270：点4+面18（正左下对应->9+后右上对应->9）+边4=26

所以最后的答案为：
$L=\dfrac{1}{24}(K^{74}+K^{20}*3*2+K^{38}*3+K^{38}*6+K^{26}*4*2)$

代码：

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const LL mod=10007;

LL sw(LL a,LL b){
    LL ans=1;
    while(b){
        if(b&1)ans=ans*a%mod;
        a=a*a%mod;b>>=1;
    }return ans;
}

LL inv(LL a){return sw(a,mod-2);}

int main(){
    int t;scanf("%d",&t);int ca=0;
    while(t--){
        LL K;scanf("%lld",&K);
        printf("Case %d: %lld\n",++ca,(sw(K,74)+sw(K,20)*6+sw(K,38)*3+sw(K,38)*6+sw(K,26)*4*2)%mod*inv(24ll)%mod);
    }
}

$\\$

---

$\\$

Polya+jave大数：hdu1812

n*n涂K色，同构：旋转翻转，求方案数

这题就比较水了，不翻转时有：

• 旋转0：n*n
• 旋转90或270：n奇时$\frac{n^2+3}{4}$，n偶时$\frac{n^2}{4}$，因为n偶时$4|n^2$，所以可以直接用$\frac{n^2+3}{4}$
• 旋转180：n奇时$\frac{n^2+1}{2}$，n偶时$\frac{n^2}{2}$，同理，直接用$\frac{n^2+1}{2}$

翻转后有：

• 偶数的左右翻转和上下翻转为：$n^2/2$;
• 其他（偶数对角线，奇数上下左右对角线）为：$(n^2+n)/2$

写成c语言的话，答案就是：

#define a^3 a*a*a
ans =( k ^ (n*n) ) 
    +( k ^ ((n*n+3)/4) )*2
    +( k ^ ((n*n+1)/2) )
    +( k ^ ((n+1)*n/2) )*2
    +( (n%2) ? ( k ^ ((n+1)*n/2) ) : ( k ^ (n*n/2) ) )*2

jave代码：

import java.util.*;
import java.math.*;

public class Main{
    public static void main(String argv[]){
        Scanner cin=new Scanner(System.in);
        while(cin.hasNext()){

            int n=cin.nextInt();
            BigInteger k=cin.nextBigInteger();
            BigInteger ans=BigInteger.valueOf(0);

            ans=ans.add( k.pow(n*n) );
            ans=ans.add( k.pow((n*n+3)/4).multiply(BigInteger.valueOf(2)) );
            ans=ans.add( k.pow((n*n+1)/2) );
            ans=ans.add( k.pow((n+1)*n/2).multiply(BigInteger.valueOf(2)) );
            if(n%2==1)
                ans=ans.add( k.pow((n+1)*n/2).multiply(BigInteger.valueOf(2)) );
            else 
                ans=ans.add( k.pow(n*n/2).multiply(BigInteger.valueOf(2)) );
            ans=ans.divide(BigInteger.valueOf(8));
            System.out.println(ans);
        }
    }
}

$\\$

---

$\\$

环形Polya：poj 2154

一个n个点的环形，有n种颜色可涂，同构情况只有旋转，n最大1e9

首先用上面那个公式 $L=\frac{1}{n}\sum_{i=0}^{n-1}n^{gcd(n,i)}$，怎么优化呢？

有关gcd的题目，普遍的做法就是以gcd=x为中心，求有多少对(n,i)的gcd=x

以前GuGu函数那题讲过了(i,j)的两种做法，现在j固定了，只剩下一个在变了。

做法一：

容斥因子，求出gcd=2k的情况，再减去4k，6k就得到了gcd=2的情况，这里就不做细说了

做法二：

做一下公式的推导：

$$L=\frac{1}{n}\sum_{i=0}^{n-1}n^{gcd(n,i)}$$
$$L=\frac{1}{n}\sum_{x|n}n^x\sum_{i=0}^{n-1}[gcd(n,i)=x]$$
$$L=\sum_{x|n}n^{x-1}\sum_{i=0}^{n-1}[gcd(n/x,i/x)=1]$$
$$L=\sum_{x|n}n^{x-1}\sum_{i=0}^{\frac{n-1}{x}}[gcd(n/x,i)=1]$$

显然，$\sum_{i=0}^{\frac{n-1}{x}}[gcd(n/x,i)=1]$表示有多少个小于$n/x$的与$n/x$互质的数，这不就是欧拉函数的定义嘛，所以答案为：

$$L=\sum_{x|n}n^{x-1}\phi(n/x)$$

#include<iostream>
#include<string.h>
#include<stdio.h>
#include<math.h>
using namespace std;
#define LL long long
const int N=32000;
int P;

bool vis[N];
int pri[N>>1],now;
void init(){
    now=0;
    for(int i=2;i<N;i++){
        if(!vis[i])pri[++now]=i;
        for(int j=1;j<=now&&pri[j]*i<N;j++){
            vis[pri[j]*i]=1;
            if(i%pri[j]==0)break;
        }
    }
}

int phi(int x){
    int res=x,a=x;
    for(int i=1;i<=now&&pri[i]*pri[i]<=a;i++){
        if(a%pri[i]==0){
            res=res-res/pri[i];
        }
        while(a%pri[i]==0)a/=pri[i];
    }
    if(a!=1)res=res-res/a;
    return res%P;
}

LL sw(LL a,LL b){
    LL ans=1;a%=P;
    while(b){
        if(b&1)ans=ans*a%P;
        b>>=1;a=a*a%P;
    }return ans;
}

int main(){
    init();
    int t;scanf("%d",&t);
    while(t--){
        LL ans=0;
        int n;scanf("%d%d",&n,&P);
        for(int i=1;i*i<=n;i++){
            if(n%i)continue;
            int ph=phi(i);
            ans=(ans+sw(n,n/i-1)*ph%P)%P;
            if(i*i!=n){
                ph=phi(n/i);
                ans=(ans+sw(n,i-1)*ph%P)%P;
            }
        }
        printf("%lld\n",ans);
    }
}