leetcode 盛最多水的容器

目录

题目描述： 

第一种解题思路：

C++代码：

第二种思路：

C++代码：

python代码：

---

题目描述： 

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

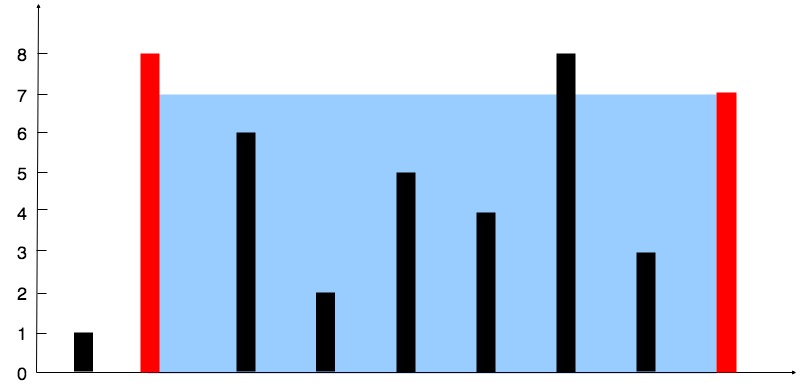
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

第一种解题思路：

 最简单的方法就是遍历所有可能，每两个柱子算一个面积。

当柱子接近2^5个时，超时错误：

C++代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        // (i, a), (j, b): area = abs((i - j) * (a - b))
        int area = 0;
        int max_area = 0;

        // C22，每次取两个直线，遍历
        for (int i = 0; i < height.size()-1; i++)
            for (int j = 1; j < height.size(); j++)
            {
                area = abs((i - j)*min(height[i], height[j]));
                if (area > max_area) max_area = area;
            }
        return max_area;
    }
};

第二种思路：

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择，就能得到问题的答案。

双指针。

参考：

力扣https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/

举个栗子：1 3 8 4 7，一开始而言，当前最优选择是选择最边上两个数，宽度最宽，用两个指针指向左右两端1和7，然后选择移动哪个指针。

（1）左边高度小于右边，此时如果如果固定左指针，移动右指针，此时宽度变小，高度即使变大，面积也是变小的，因为面积由小的一端（左端是1）决定。即如果固定左边，移动右边，面积不会变大。也就是说左端1和其他任何搭配，面积都不会变大，所以可以排除1，即只能移动左端；

（2）移动左端后，现在左右分别指向3和7，更新面积后，再次确认移动哪一端。同样，3和其他任何搭配，面积也不会变大，排除3，即只能移动左端。发现每次移动都是高度小的那一端。

再举个栗子：7 3 8 4 1

（1）同理，右边更小，如果固定右端1，移动左指针7，宽度变小，右端高度即使变大，面积也是由左端1决定，即面积不会变大，也就是右端1和左端其他任何搭配，面积都不会变大，所以排除1，只能移动右指针（值偏小的那端）；

不断移动左右指针，边搜索边更新最大面积，直到左右指针相遇，结束。

所以移动两个指针，哪边小就移动哪个。

C++代码：

执行用时：60 ms, 在所有 C++ 提交中击败了96.57%的用户

内存消耗：57.7 MB, 在所有 C++ 提交中击败了9.31%的用户

通过测试用例：61 / 61

class Solution {
public:
    int maxArea(std::vector<int>& height) {
        
        int max_area = 0;
        // 左右指针，移动高度小的那一端，然后更新面积，直到左右指针相同
        int left = 0, right = height.size()-1;

        while (left != right)
        {   
            // 看是否需要更新最大面积
            int cur_h = (height[left] < height[right])?height[left]:height[right];
            int cur_area = (right-left) * cur_h;
            if (cur_area > max_area) max_area = cur_area;
            // 移动最小高度那端，看是否有更大面积组合
            if (height[left] < height[right]) left++;
            else right--;
        }
        return max_area;
    }
};

python代码：

执行用时：120 ms, 在所有 Python 提交中击败了64.23%的用户

内存消耗：21 MB, 在所有 Python 提交中击败了75.91%的用户

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        max_area = 0
        left = 0
        right = len(height) - 1
        while left != right:
            area = (right - left) * min(height[left], height[right])  # 当前位置的面积
            if area > max_area: max_area = area  # 当前面积更大，则更新最大面积。
            if height[left] > height[right]:  # 继续搜索其他位置
                right = right - 1
            else:
                left = left + 1
        return max_area