02 如何训练网络？深入理解反向传播

在01 深度学习基础及前向传播中，我们已经搭建好了一个基础的三层神经网络架构，如图：

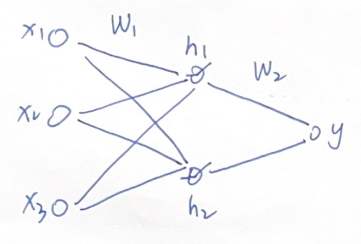
它由三个输入features：x1、x2、x3，一个输出：y，中间的hidden layer包含两个nodes，采用ReLU作为激活函数。

其前向传播的计算过程为：

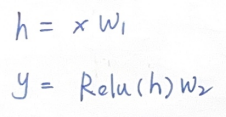
已知的数据如下，输入矩阵x中，列向量对应每一个feature，行向量储存每条sample，共有n条samples，它们对应的输出储存在输出向量y中。

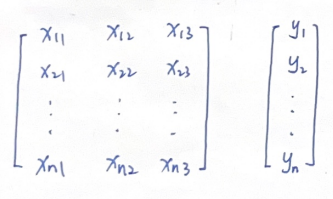
在输入数据已经经过归一化处理的情况下，偏置项b的作用被削弱，此时可以考虑忽略偏置项。因此，为了简化计算流程，后续分析中暂不考虑偏置项b，不影响我们对整体流程的理解。

如何通过这些大量的数据，去”训练“这个神经网络，使得它能很好的反映输入x和输出y之间的关联？

这里我们关注两点：

1. 这个神经网络的structure，包含输入输出项、层数、隐藏层节点数量、激活函数，这些都是在训练之前已经搭建好的，训练的时候不会再去调整。那么我们能”训练“的，或者说能够进行调整的，只有那些参数项，也就是W1，W2。
2. ”一个能很好反映输入x和输出y之间关联的神经网络“，如果一个神经网络能够精准地呈现输入 x 与输出 y 的内在联系，那么当把输入 x 放入该神经网络进行运算处理后，所得到的预测值 y^ 将会非常接近真实值 y。

理解了这两点，上面的问题就变成了：
如何调整神经网络的参数项W1、W2，使得输入x通过神经网络计算后得到的预测值y^和真实值y的差距最小。

几乎所有深度学习的任务，核心都是这个问题。

均方误差Mean Squared Error（MSE）

首先我们需要知道如何定义”预测值y'和真实值y的差距“，在深度学习中常用的误差定义方式是均方误差Mean Squared Error，其计算方法如下：

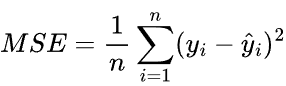
其中n表示n个samples，y表示真实值，y^表示预测值。

我们先将关注点放在已知数据的第一组sample，输入x = ( x11, x12, x13 )，输出y1。
通过前向神经网络，得到了当前的预测值，并将它带入到MSE中，得到了误差项L：

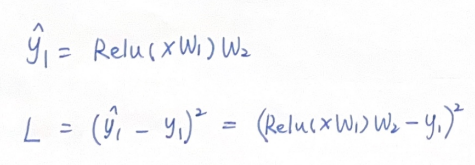
其中，x1和y1是已知的真实数据，W1，W2是模型参数。

这里的L就是损失函数（loss function），也有一些教材中称之为目标函数（objective function），它是衡量模型预测结果与真实结果之间差异的函数，它得到的数值越小，说明模型的预测结果越接近真实结果，模型的性能也就越好。

现在，问题进一步转化为：
如何调整神经网络的参数项W1、W2，使得预测值y^和真实值y的损失函数L最小。
此时L是一个关于W1、W2的函数，这是一个经典的优化问题。

梯度下降Gradient Decent

梯度下降原理是求解优化问题的经典方法，先来看一个简单的例子：

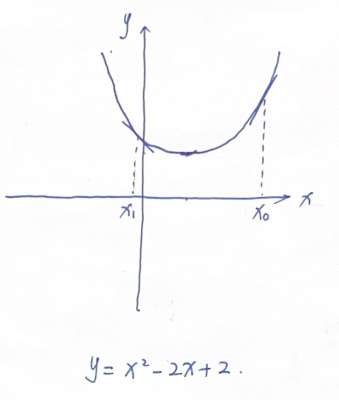
我们希望求解x的值，使得y最小。
用优化的思路去求解，我们初始化一个随机的x0，如何移动x0，才能让它到达函数最低点呢？

从函数曲线上我们可以直观的看到：在最低点右侧的x0，我们希望将它向左移动，从而到达最低点；而在最低点左侧的x1，我们希望将它向右移动，以达到最低点。同时我们也发现，最低点的左右两侧，其斜率符号相反，在最低点右侧，斜率为+；在最低点左侧，斜率为－。

这说明，函数y关于x的斜率，“刚好”能够帮助我们判断如何移动当前x，使得它往最低点方向移动。

因此，这个求解优化问题的步骤如下：

1. 初始化一个x0，作为当前x取值
2. 在当前x取值处，求y关于x的导数
3. 利用导数指导我们更新x：

   

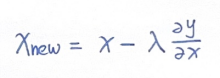
其中，λ是更新步长，控制着更新速度。y关于x的导数如果为正，则x减小，向左移动；反之，导数为负，则x增加，向右移动。

1. 重复第2、3步骤，直到y的值不再发生显著变化，此时的x取值，使得y最小。

所以这是一个通过曲率计算，不断迭代更新输入x，使得y逐步下降，最终达到最小值的过程。

如果存在多个输入，y = f(x1, x2)，此时函数方程不再是一条曲线，而是多维空间中的一个曲面：

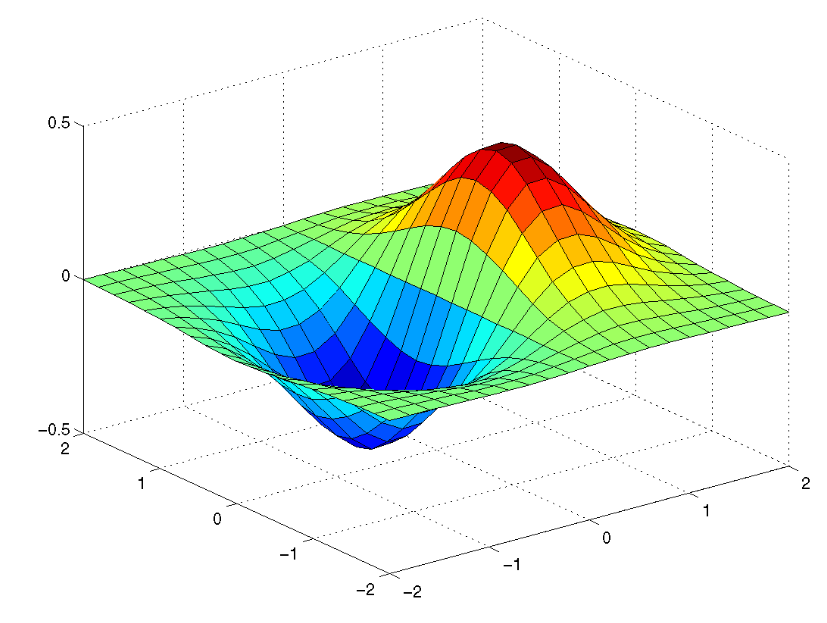
对应的“曲率”为一个向量：

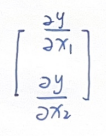
这个向量，依然可以帮助我们判断如何移动当前输入（x1，x2），使得它逐步往曲面的最低点移动。这个向量，我们称之为梯度（Gradient）。

因此，这种通过梯度来迭代更新输入量，从而计算函数最低点的方法，叫做梯度下降算法。

如何更新参数项W1、W2，使得损失函数L最小。也是一个这样的梯度问题。那么如何计算L关于W1、W2的梯度呢？

注意在神经网络模型中，输入和输出是观测量、已知量，而参数项W1、W2是可变量，是需要优化的量。因此我们是对这些参数项进行求导。
而上述优化y = f(x1, x2, x3)过程中，输入x1、x2、x3是可变量，我们对这些量进行求导。
这就是为什么我们优化神经网络模型时对参数量进行求导，而优化y = f(x1, x2, x3)时是对输入量进行求导。关键在于搞清楚函数是关于哪些可变量的函数，是需要对哪些量进行调整以达到优化目的。

链式法则Chain Rule

神经网络的预测过程是一个复合函数，复合函数的求导遵循链式法则。
y=f(u)且u=g(x)，则dx/dy​=du/dy​⋅dx/du​

用一个具体的例子来说明，假如我们看这样一个极简网络架构以及它关于参数的求导过程：

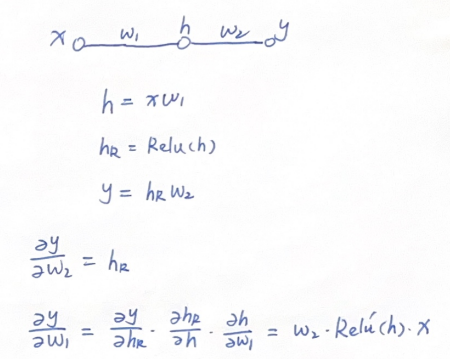
其中，ReLU函数也是链式求导过程中的一环，其导数可表示为：

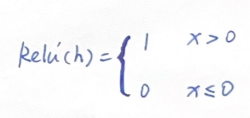
那么问题来了，上文中我们需要得到的是损失函数L关于W1、W2的梯度，从而让损失函数最小。在这里为什么要计算输出y关于各参数的导数呢？

如果你再观察一下损失函数的表达式，就会发现，损失函数L也是关于输出y的函数。

也就是说，从输出y到损失函数L，相当于在我们的神经网络计算之后又增加了一层计算。同样的，也是在求导链中增加了一环。

事实上，在我初学反向传播时，为了便于理解，我会在神经网络示意图中把激活函数、损失函数都显式的绘制出来，像这样：

能够更加清楚的看到各层之间的函数关系：

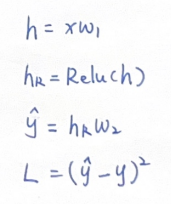
这时候我们再用链式法则求导：

注意这里导数计算结果前面的标量乘积2通常可以省略，因为这里的导数本质上是用它的符号（正/负）来指导我们往哪个方向去移动变量，它主要是对移动方向进行把控，而移动的多少我们用一个λ参数来控制，叫做步长。

反向传播过程整理

我们把上述对这两个参数w1和w2求导的计算反映到如下的示意图上：

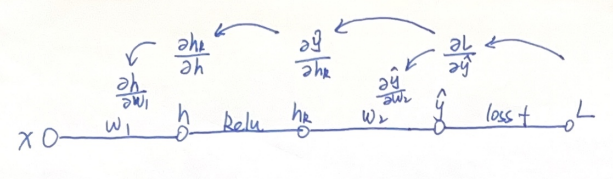
由于链式法则的存在，结合求导的计算公式，这一过程可以看作从图中右侧的“L对y^求导”开始，不断向左，一层一层进行链式求导。由于这些复合函数的导数之间是相乘关系，我们可以把这一过程看作是把导数向左进行“传播”，这也就是反向传播这一名称的由来。

在y处，这一传播过程分为了两支，一支通过“y对w2”求导，得到了L对w2的导数。
另一支则继续向h左，最终传播到w1，得到了L对w1的导数。

在上面的反向传播过程整理中，我们一直都是采用单输入，单输出的节点模型，如果我们的输入是多个features，输出也是多个outputs，中间层的节点也有多个，权重也从scalar变成了权重矩阵。这种情况下，我们怎么求导？

这就涉及到向量/矩阵的求导问题。

向量/矩阵求导

我们针对多输入多输出多节点的模型，绘制这样一个示意图进行研究：

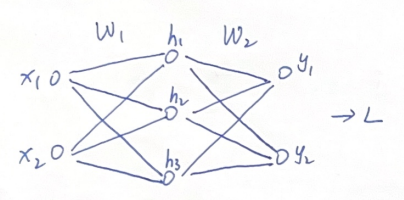
前向传播计算：

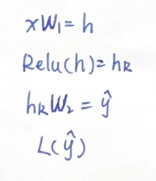
我们将相关的向量和矩阵展示出来：

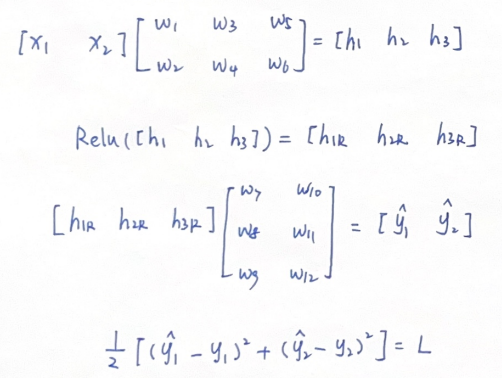
结合上文的反向传播过程，我们发现需要考虑一些新的"导数"类型：

• 标量对向量的导数，如L对y^的导数
• 向量对向量的导数，如y^对hr的导数
• 向量对矩阵的导数，如y^对W2的导数

导数的本质是研究一个变量的变化如何影响另一个变量进行变化。
dy/dx，研究的是x(单变量)的变化如何影响到y(单变量)的变化。

而向量、矩阵，只不过是标量的某种结构化的集合。我们还是可以将其拆解成单变量的的导数。

标量对向量的导数

标量对向量的导数，研究的是向量中每个元素的变化，如何影响标量的变化

向量对向量的导数

向量对向量的导数，研究的是一个向量中每个元素的变化，如何影响另一个向量中每个元素的变化

这个矩阵，也叫雅可比矩阵（Jacobian Matrix）。

当我们尝试把矩阵展开去求解每一个元素时，会发现其刚好就是系数矩阵W2的转置。

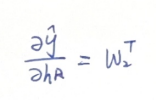
向量对矩阵的导数

向量对矩阵的导数，这个相对比较复杂，而且不容易向上面两种形式一样融入链式求导法则，但如果我们将其拆开来，直接利用元素层面的链式法则，观察L对每个矩阵元素的导数，同样可以找到一些规律，使得我们借用矩阵简化反向传播。

例如：y^对W2的导数，我们直接从L对W2的导数定义开始分析：

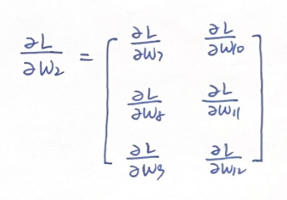
由于w7仅关联了y1，同理W2中各元素和y1，y2^都是单向关联，因此我们的导数矩阵可以写为：

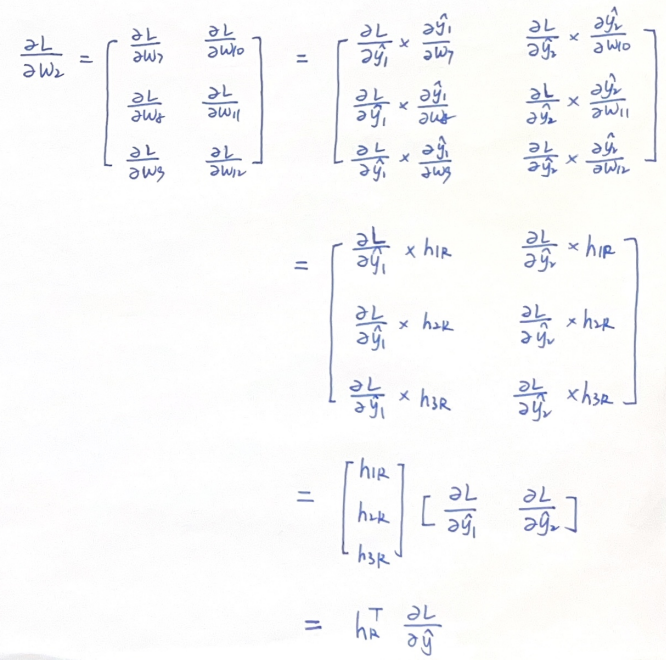
因此，L对W2的导数，相当于L对y^的导数，左乘一个hr向量的转置。
同理，如果我们看L对W1的导数，也可写为L对h的导数，左乘一个x向量的转置。

我们进行一次比较完整的反向传播计算过程：

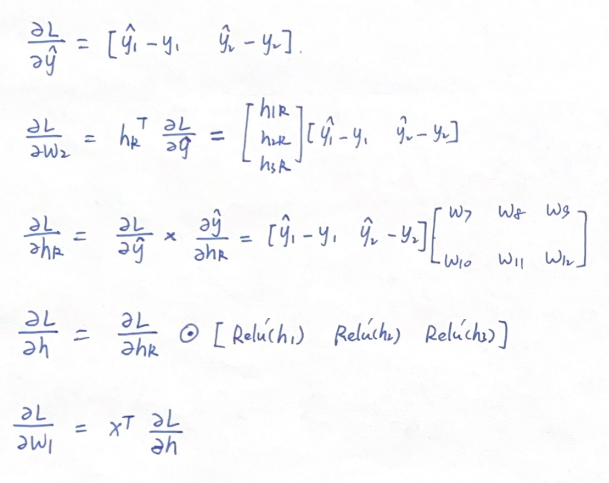
综上，我们得到了损失函数L分别关于W1和W2两个矩阵的导数。现在，我们就可以用这个两个导数矩阵对W1和W2进行更新了。

再看整个训练流程

我们再看文章开头的例子，整体梳理一遍模型训练的流程。

1. 初始化W1，W2参数矩阵
2. 把第一条sample输入神经网络进行前向传播，得到预测值y^，并通过损失函数算出当前误差
3. 通过反向传播，得到损失函数关于W1和W2参数矩阵的梯度
4. 用得到的梯度分别更新参数矩阵W1和W2
5. 重复第2-4步，用下一条sample训练神经网络。直到损失函数值小于预设，或者迭代达到一定次数，训练结束。

这种每次使用单个sample进行参数矩阵更新的方法叫随机梯度下降（stochastic gradient descent，SGD）。这样的学习速度较快，处理大规模数据集时更为高效。
如果每次采用多个sample进行梯度更新，则称之为批量梯度下降(Batch Gradient Descent，BGD)，每次采用的多个sample称为一个batch。
如果一次采用全部samples进行梯度更新，则称之为Full Batch Gradient Descent。如果没有特别说明，在深度学习中，Gradient Descent 通常默认指 Full Batch Gradient Descent