线性模型在分类中的应用
前面一共介绍了三种线性模型:线性分类,线性回归,逻辑回归 。三种模型有一个共同特点都需要计算一个得分:s=wTxs=w^Txs=wTx,线性分类对得出分数进行取正负号操作;线性回归直接输出得分结果;逻辑回归通过sigmoid函数映射得出概率。

其中线性分类的误差是一个NP-hard问题,目前没有好的方法进行求解,那么能不能用逻辑回归或者线性回归来帮助线性分类解决这个问题呢?先来回顾一下三种模型的误差计算方式:

将输出空间视为二元分类的情况也即:y=y=y={-1,+1},对误差函数进行变形:
- 线性分类:err0/1=∣sign(s)≠y∣=∣sign(ys)≠1∣err_{0/1}=|sign(s)\neq{y}|=|sign(ys)\neq{1}|err0/1=∣sign(s)=y∣=∣sign(ys)=1∣
- 线性回归:errSQR=(s−y)2=(ys−1)2err_{SQR}=(s-y)^2=(ys-1)^2errSQR=(s−y)2=(ys−1)2
- 逻辑回归:errCE=ln(1+exp(−ys))err_{CE}=ln(1+exp(-ys))errCE=ln(1+exp(−ys))
三种模型的误差经过变形都和ysysys有关,那么ysysys代表了什么物理含义呢 ?sss为得分, y=y=y={-1,+1},也就是说 ys的值越大,正确得分就越高。预测结果和真实情况就越接近。接下来用图形化的方式来表现三种模型的误差函数:

将ysysys作为横坐标,误差作为纵坐标。画出对应误差函数的图像,其中红色的线为线性回归的误差函数通过图像可以清楚的发现其误差只有在某一点最小,ysysys过大或者过小都会影响准确率。蓝色的线为线性分类函数的误差,当ysysys大于0时,ysysys就是0。最后黑色的线为逻辑回归的误差,随着ysysys的增大逐渐减小,最终会趋于0.
线性回归的误差函数始终在线性分类之上,如果用线性回归函数的误差来代替线性分类函数的函数,从理论上来看没有问题。但是,线性回归的误差函数在ysysys过大或者过小的情况下,都会产生较大的误差上限。
逻辑回归函数的误差与线性分类的比较相似。但是,美中不足的是逻辑回归的误差在0的附近在线性分类之下。所以,他并不能成为误差上限函数。
可以将逻辑回归的误差函数向上平移一点:

如上图所示,这样逻辑回归的误差就可以用来作为线性分类的误差上限。
把平移后的误差称为:errSCEerr_{SCE}errSCE,其变化过程如下图所示:

在由VC限制理论进行分析:

最终可以得到如下公式:

经过以上分析我们可以得出一个结论:利用逻辑回归得出在输出空间为{-1,+1}的www,在将其带入sign()sign()sign()函数,得到最优假设函数sign(wTx)sign(w^Tx)sign(wTx)
对三种模型进行一个简单的比较:

通常用线性模型获得初始的w0w_0w0然后在利用逻辑回归进行更新 。
两种梯度下降方法
更新错误的方式为:

先回顾一下PLA,我们更新的方式是:当遇到犯错的的点时,就以犯错误的点为起点,做出一条更好的线,向犯错误的点靠拢,尽量把他分到正确的类别。利用这种方式,只需要将所有的样本点迭代一次就可以完成分类任务,找出最好的线www。算法执行的时间复杂度为:O(1)O(1)O(1)
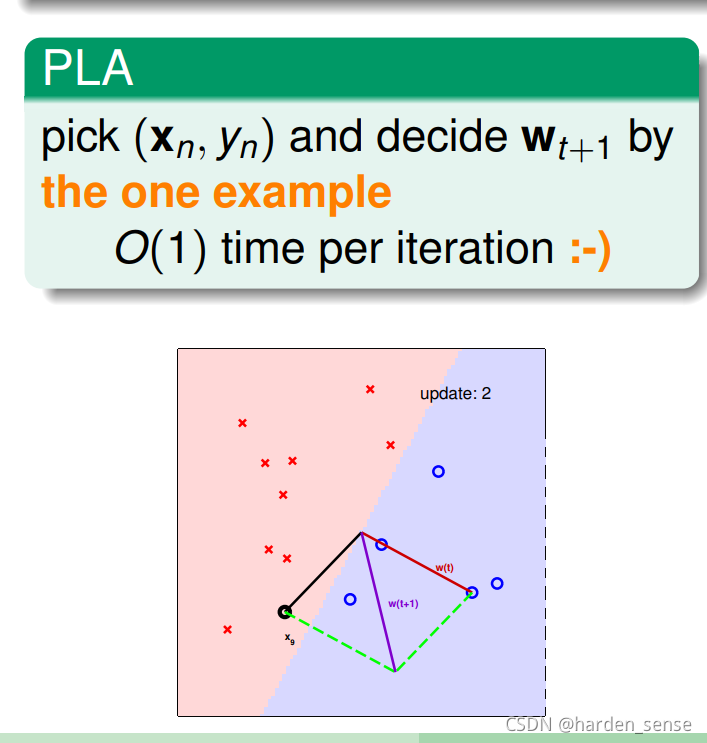
如果用逻辑回归的方式来更新www,花费的时间复杂度和pocketpocketpocket类似,针对每一个可能的www都需要将样本点检测一遍,花费的时间为O(N)O(N)O(N)。那么能不能想个办法让逻辑回归的时间复杂度也是O(1)O(1)O(1)。
逻辑回归的更新方式:

每更新一个新的www,我们要计算所有点的方向向量的平均值。这个平均值的计算浪费了大量的时间。可以这样做,就像抽样检测那样,随机的从样本点中选择一个点来代替所有点的平均值。称这种方式为随机梯度下降(SGD)。


随机梯度值可以看做真实的梯度值加上一个噪音,这种替代的理论基础是在迭代次数足够多的情况下,平均的随机梯度和平均的真实梯度相差不大。
该算法的优点是简单,容易计算,适用于大数据或者流式数据;缺点是不稳定,每次迭代并不能保证按照正确的方向前进,而且达到最小值需要迭代的次数比梯度下降算法一般要多。
PLA与SGD两种算法的对比。

逻辑回归的随机梯度下降类似于一种特殊的PLA,原因是梯度更新中权重的更新方向θ(−ywnTx)\theta(-yw_n^{T}x)θ(−ywnTx)的值并非0或者1,而是0-1之间的值。当学习率η=1\eta=1η=1并且wTxw^TxwTx很大的时候,逻辑回归的梯度下降就相当于PLA.
SGD需要调节两个参数:迭代步棸和学习率,迭代步棸不好确定,只能假设在有限步后,能够做的足够好。学习率也不好确定,只能根据不同的设计场景,参考别人的经验,选择一个较好的学习率。
利用线性回归进行多分类
在现实生活中,我们不仅仅会遇到二分类问题,还会遇到多分类问题。

输出空间yyy有四类,即y=[□,◇,△,☆]y=[□,◇,△,☆]y=[□,◇,△,☆],可以用二元分类的思路进行处理,将问题进行分解。首先将问题简化为:是否为□。生成一个新的二元分类问题Y=[□=○,◇=×,△=×,☆=×]Y=[□=○,◇=×,△=×,☆=×]Y=[□=○,◇=×,△=×,☆=×],通过这种方式得到一个分类面:
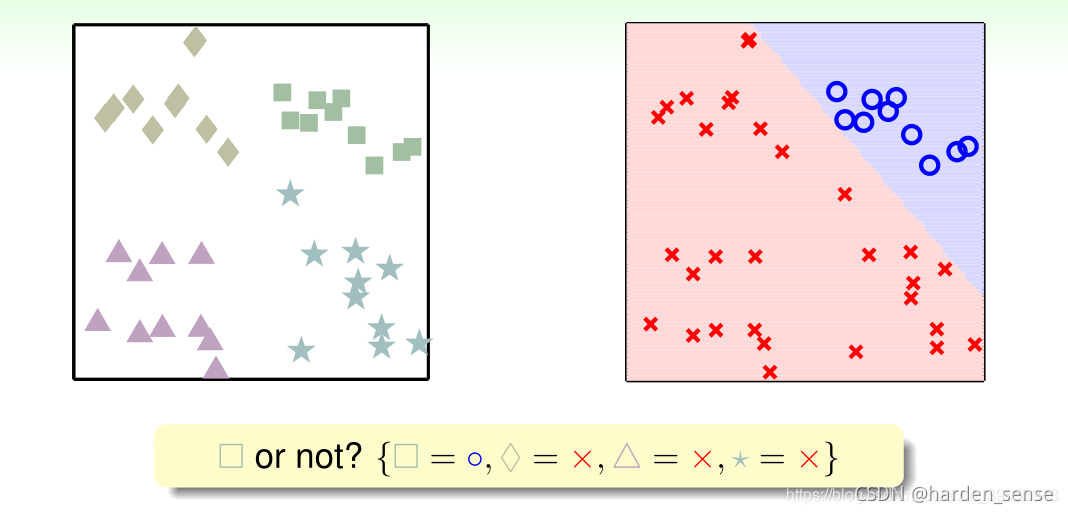
同样的道理将其他三种图形也进行分类:

四种分类的结果为:

综合四种分类结果可得:

可以看到,有一些无法处理的情形。其中,四个边缘的三角阴影区域为相邻两个类别都争夺的区域,图正中的菱形区域不属于任何类别。这些问题如何解决?
使用软分类,还是关于类别 □ 的二元分类问题,此处不再使用硬划分,而是使用该样本点是 □ 的可能性,即P(□∣x)P(□|x)P(□∣x),如下图所示:

其余情况同理,四种类别的“软”二元分类情况如下图所示:

那么应该如何判断样本点属于哪个类别?可以分别计算样本点在四种软二元分类情况下概率,选择其中概率最大的一个作为所属类别,计算公式如下:
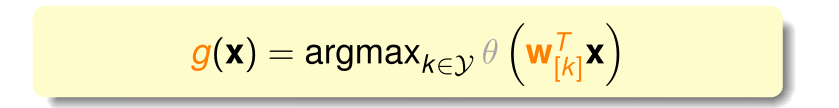
公式使用逻辑回归函数求 概率,k表示种类,由于sigmoid的函数单调函数,因此可以直接比较类别的得分值。这种方法称为**一对多(OVA)**算法流程如下:

该算法的优点是,易于将线性回归的二元分类问题扩展成为多类;缺点是当类别特别多时,产生了不平衡现象(如类别特别多+1的数据就会很多,-1的数据就会很少,数据严重不平衡)
利用二元分类进行多分类
针对OVA在类别非常多的情况下训练数据严重失衡的问题,介绍一种应对这种问题的解决方案。
在四分类问题中,不像OVA在整个数据集中计算是否为□的权值向量w,这种方法在四类中任选两类,。将两类的值设为+1和-1,在包含两类的数据集上计算权重向量w。

其它情况同理,从四种类别中选取两种做二元分类,一共可得6种(C42C_4^2C42)二分类情况,结果如下:

那么,如何判断某新进样本属于哪个分类?由上例分析,6次二分类之后,如果数据集中的一个样本,有三个分类器判断它是正方形;一个分类器判断是菱形;另外两个分类器判断是三角形;那么取最多的那个,即判断它属于正方形,至此分类完成。
将以上6种二分类组成分类器进行分类,分类结果如下图所示:

这种分类方式称为一对一(One Vervuse One, OVO)。其算法流程如下:

-
从所有类别中任选两个进行二分类,共产生CK2C_K^2CK2种分类情况;
-
在数据集D上求出最佳的权值向量w[k,l]w_{[k,l]}w[k,l]
-
通过投票返回假设函数 g
这种方法的优点是更加高效,每次使用两类的训练数据,然后根据投票机制汇总不同的二分类结果,虽然分类次数增加,但是单次分类的数量减少,一般不会出现数据不平衡的情况。缺点是需要分类的次数多。时间复杂度更O(K2)O(K^2)O(K2)





 本文探讨了线性模型如何通过逻辑回归的误差函数优化线性分类,并介绍了OVA(一对一)和OVO(一对多)策略在多分类问题中的应用,讨论了它们的优势与不足,以及如何处理数据不平衡问题。
本文探讨了线性模型如何通过逻辑回归的误差函数优化线性分类,并介绍了OVA(一对一)和OVO(一对多)策略在多分类问题中的应用,讨论了它们的优势与不足,以及如何处理数据不平衡问题。
















 7226
7226

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








