逻辑回归
在谈逻辑回归之前,先看个列子。心脏病预测:
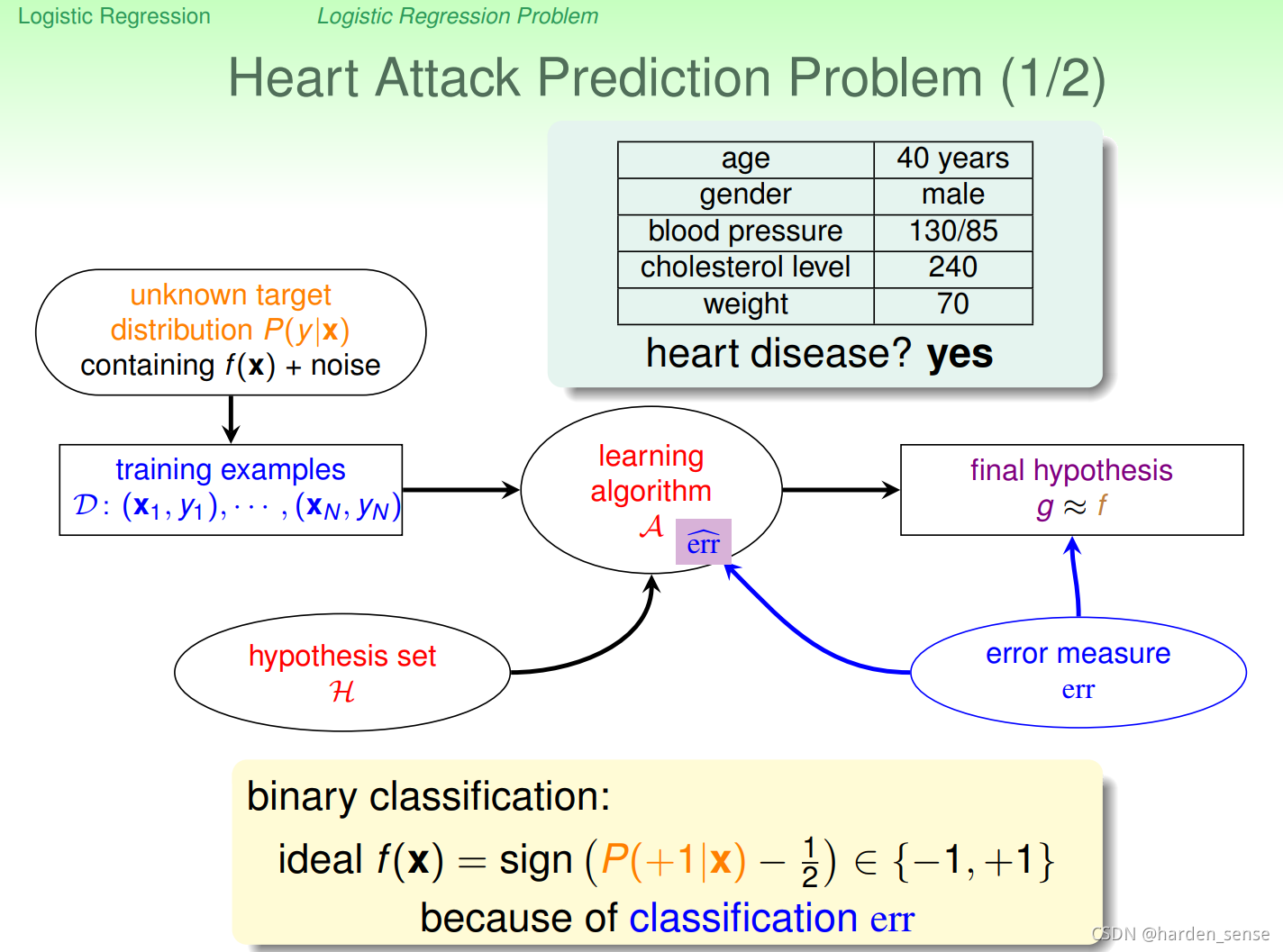 我们有某个人的相关资料,以及他是否患有心脏病。用这些资料进行训练,我们可以得到一个预测某人是否患有心脏病的模型。这是一个二元分类问题,输出空间为(−1,+1){(-1,+1)}(−1,+1),目标函数为f(x)f(x)f(x)其表达形式如图所示。但是,在实际生活中,我们并不会直接说一个人是否一定患病,通常会给出一个概率值。比如我们在看过某个人的资料后,会告诉他,你患病的概率为70%。
我们有某个人的相关资料,以及他是否患有心脏病。用这些资料进行训练,我们可以得到一个预测某人是否患有心脏病的模型。这是一个二元分类问题,输出空间为(−1,+1){(-1,+1)}(−1,+1),目标函数为f(x)f(x)f(x)其表达形式如图所示。但是,在实际生活中,我们并不会直接说一个人是否一定患病,通常会给出一个概率值。比如我们在看过某个人的资料后,会告诉他,你患病的概率为70%。
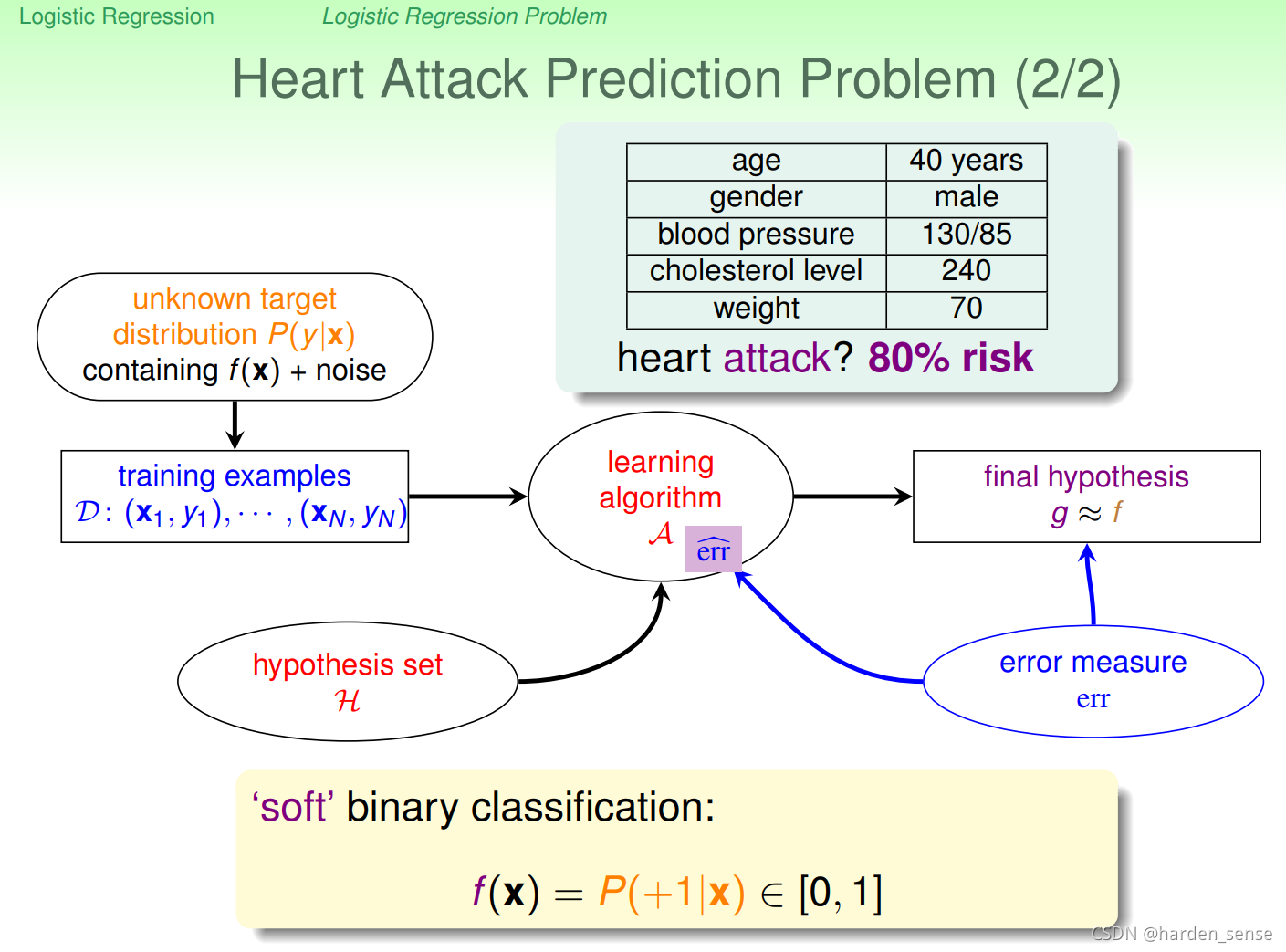
更新目标函数的输出空间为[0,1]。那么问题就来了,如果采用二元分类,我们得到是只有{-1,+1}两种结果,如果用线性回归得到的是整个实数R上的一个集合。该如何处理算法,以满足我们的需求,让输出空间在[0,1]。
针对目标函数,理想的数据集,应该是这样的:

理想数据集给出的结果是发病的概率,然而真是的数据集确实这样的:

真实的数据集只有发病和没有发病两种情况,而不会在结录结果种出现概率。
可以将真实的训练集数据视为含有噪声的理想训练数据。问题就转化为:如何用真实的数据解决软二元分类问题,假使函数该如何设计。先回顾之前线性分类和二元分类所用的假使函数,看是否能在其中得到一点启发。线性分类是我们给出特征向量:x=[x1,x2,x3....xd]x=[x_1,x_2,x_3....x_d]x=[x1,x2,x3....xd]然后计算出权重向量WWW,在根据其来进行预测。
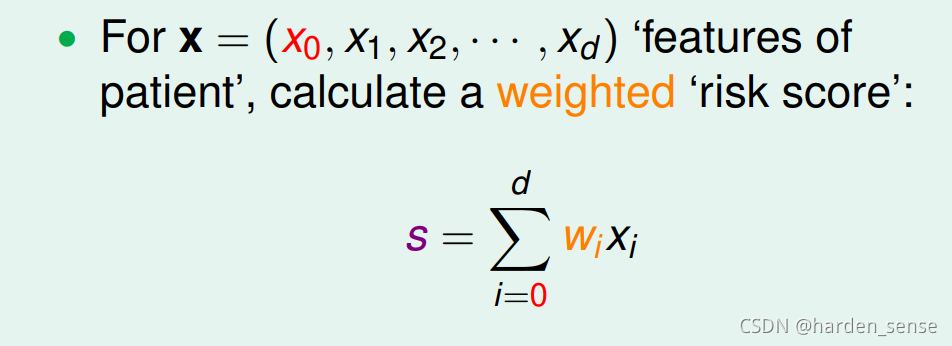
二元分类只不过是在其基础上进行了取正负号操作。我们可以采用和二元分类相似的方法来解决软二元分类问题。当sss计算出来以后,我们对sss进行某个函数映射,是他的值在0和1之间。一个非常好的选择就是sigmoid函数:
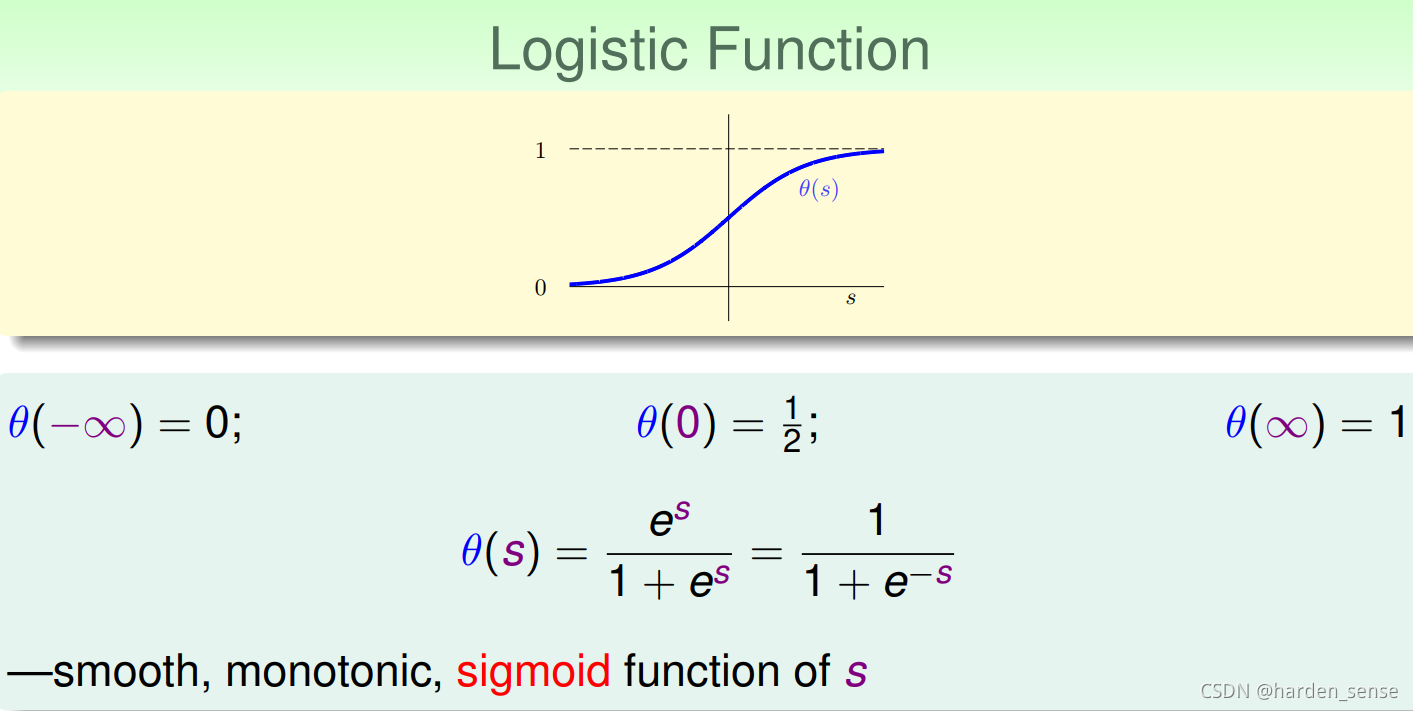
这个函数的图像如上图所示,可以实在从整个实数集R到[0,1]的映射。有个这个函数,我们就将假设函数设置为:
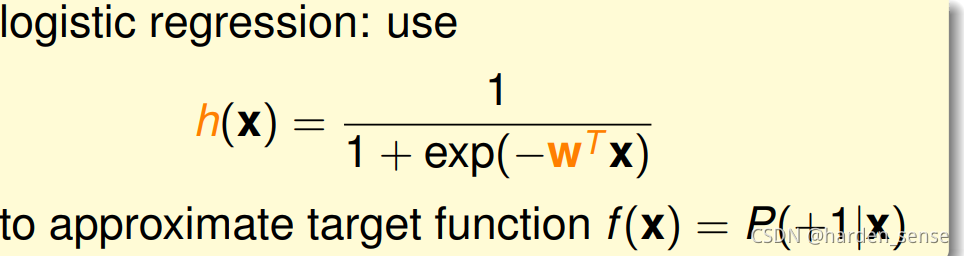
h(x)h(x)h(x)足够的接近f(x)f(x)f(x)
三种线性模型
从开始到现在我们接触了三种线性函数:二元分类,线性回归,逻辑回归:
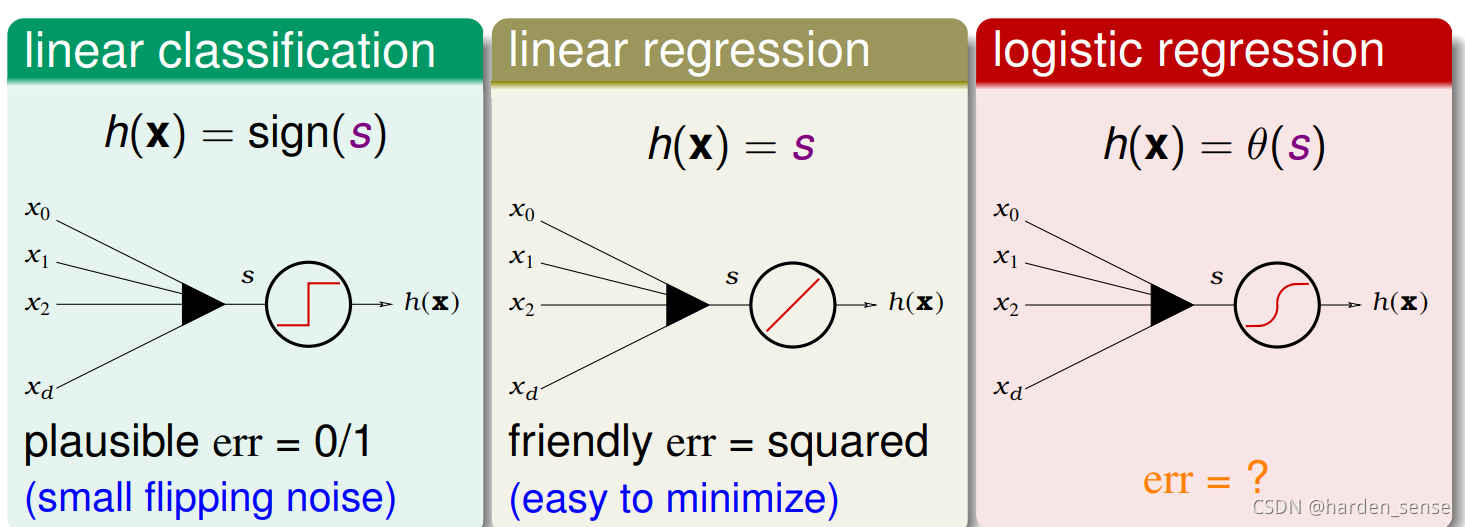
这三种函数种有一个共同点,那就是都会出现WTXW^TXWTX,前两个的错误衡量方式分别为0/1误差和均方误差。那么逻辑回归的错误该怎么衡量呢?先简单介绍一个概念似然:对于目标函数f(x)=P(+1∣X)f(x)=P(+1|X)f(x)=P(+1∣X),如果找到了假设函数很接近目标函数。也就是在假设空间h中找到了一个g与目标函数非常的接近,能和目标函数产生同样的数据集D,那么就称这个g是最大似然函数,公式如下:

由逻辑回归可以推导出下式成立:

考虑一个数据集D=D=D={(x1,+1),(x2,−1.....)(x_1,+1),(x_2,-1.....)(x1,+1),(x2,−1.....)},则通过目标函数产生此种样本的概率可以下面的式子进行表示:

由目标函数fff 对公式做如下替换:

目标函数是未知的,已知的只有假设函数,应用极大似然公式,可以用假设函数hhh替换目标函数:
likehood(h)=P(x1)∗h(x1)∗P(x2)∗)(1−h(x2))∗......likehood(h)=P(x_1)*h(x_1)*P(x_2)*)(1-h(x_2))*......likehood(h)=P(x1)∗h(x1)∗P(x2)∗)(1−h(x2))∗......
逻辑回归的假设函数h(x)=h(x)=h(x)=θ(wtx)\theta(w^tx)θ(wtx),有性质:1−h(x)=h(−x)1-h(x)=h(-x)1−h(x)=h(−x),因此可以将上式进行转化为:
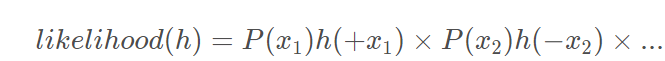
因为p(xi)p(x_i)p(xi)对于所有的iii都一样,也就是说似然函数只与每个样本的连乘有关,将真实样本输入yn(−1,+1)y_n(-1,+1)yn(−1,+1)引入公式:可以得到下面的式子成立:
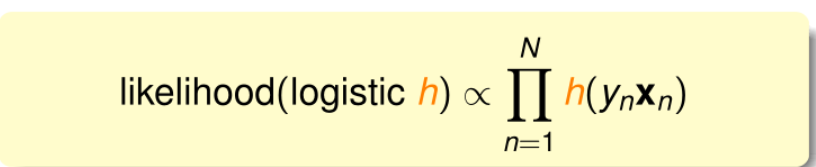
因为寻找的是最大似然函数,可以得到下面的式子:

将h(x)h(x)h(x)带入得:
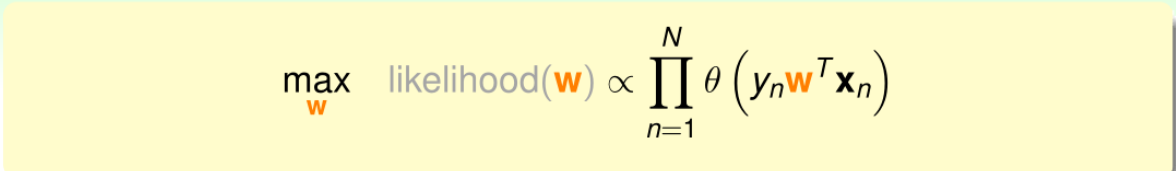
连乘不易求解,因此对上式取对数,转化为连加形式:
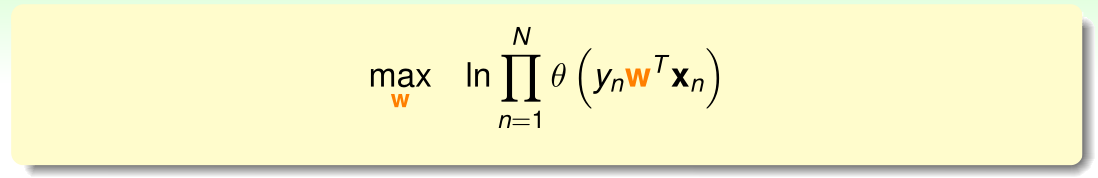
通过引入符号,将最大化问题转化为最小化问题,同时引入平均系数 1N\frac{1}{N}N1
使得公式与之前的错误衡量类似:
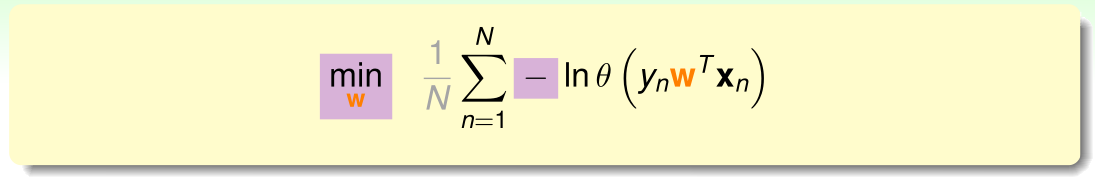
将θ(s)\theta(s)θ(s)带入上式:
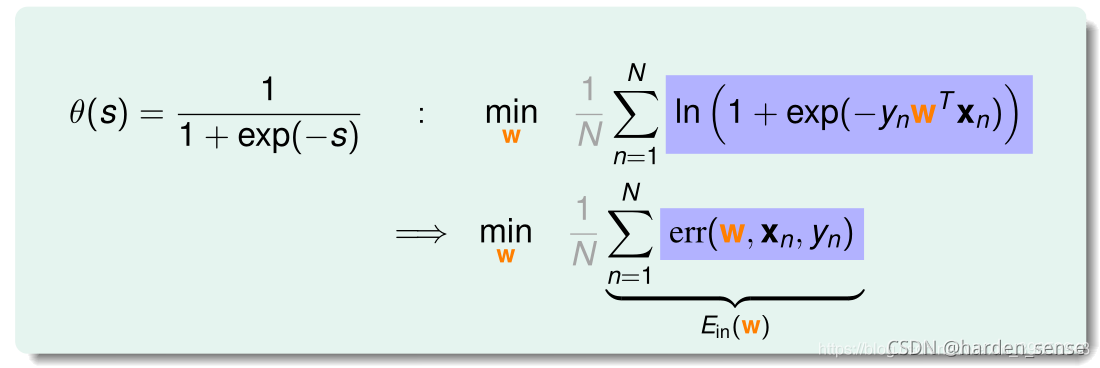
逻辑回归的误差梯度
误差的表达式已经得到,接下来要做的就是最小化这个误差。
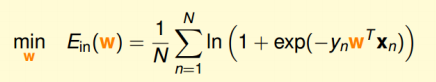
比较幸运的事情是这个误差函数是个凸函数,可以象处理线性回归的误差函数那样来处理这个函数。对他进行求导,利用微积分的相关知识就可以完成这个工作,只不过求导过程略微有点麻烦。具体求导过程如下所示:
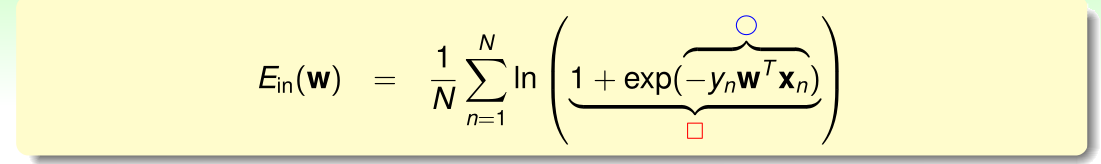
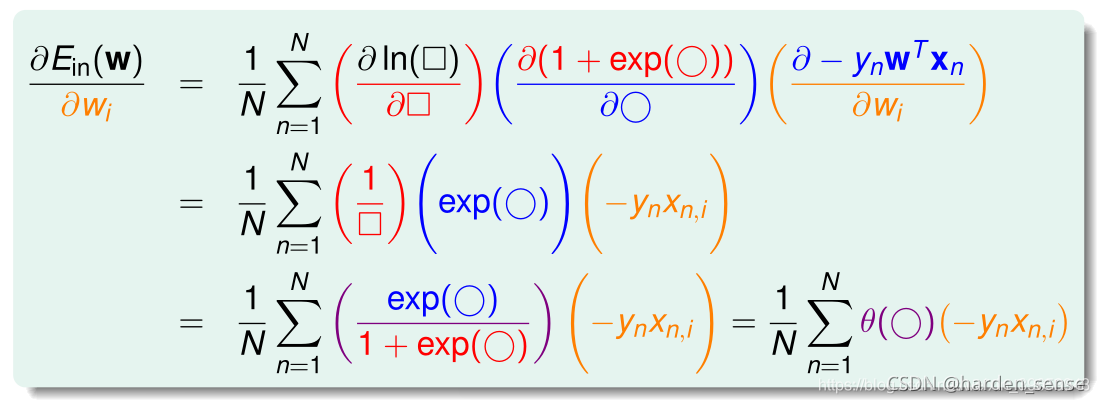
最终的计算结果为:
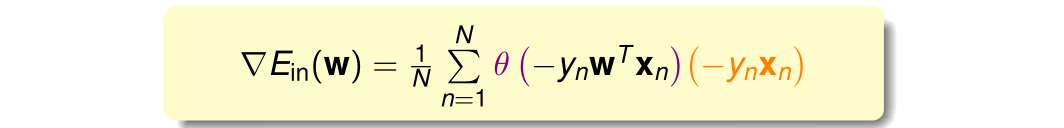
为了让误差最小,就要让最终的计算结果为0。上式可以看为θ(−ynwtxn)\theta(-y_nw^tx_n)θ(−ynwtxn)和−ynxn-y_nx_n−ynxn的线性加权,要使得这两部分的线性加权为0.有两种情况:
- 线性可分:如果所有的权重θ(−ynwtxn)\theta(-y_nw^tx_n)θ(−ynwtxn)为0,那么整个式子自然为0,使得θ(−ynwtxn)\theta(-y_nw^tx_n)θ(−ynwtxn)为0的条件是,(−ynwtxn)(-y_nw^tx_n)(−ynwtxn)小于0,也即:(ynwtxn)(y_nw^tx_n)(ynwtxn)>>根据sigmoid函数的性质整个函数值趋近于0.(ynwtxn)>0(y_nw^tx_n)>0(ynwtxn)>0也就意味着所有的预测值和真实值相同,只有线性可分才能做到。
- 线性不可分:比较麻烦,只能用迭代法进行。
在开始之前先简单回顾一下PLA的相关内容:

每次出现错误时,PLA更新了两个内容,一个是方向也即(ynxn)(y_nx_n)(ynxn)记为vvv:另一个是步长。这个概念之前没有提过,记为:η\etaη。这两个参数和终止条件决定了迭代优化算法。

梯度下降
逻辑回归求解最小误差使用类似PLA的迭代算法,通过一步步改变权值向量www,寻找使得误差最小的权值向量www,该迭代方法的公式如下:
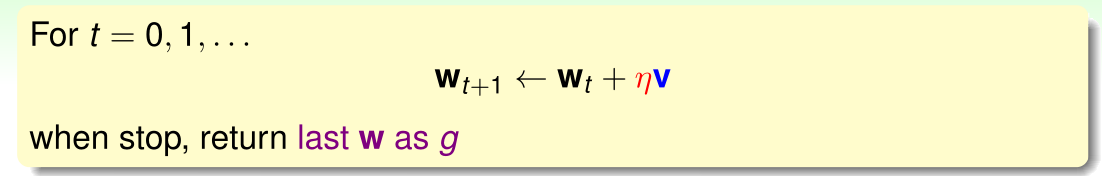
上式中,vvv表示分心的方向,η\etaη表示更新的步长。逻辑回归的误差函数是处处可微的凸函数,其曲线的谷底对应最小的误差。
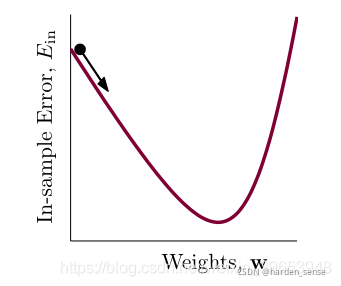
那么该如何选择这两个参数使得下降的最快,在步长确定的情况下,沿着梯度的方向下降最快,也即|vvv|=1
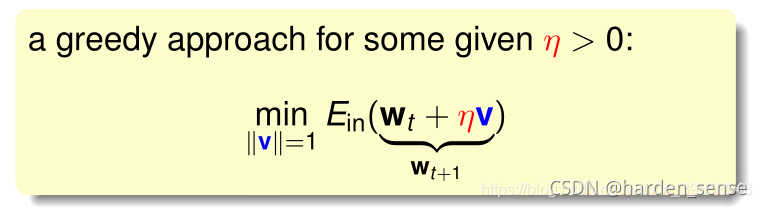
以上是非线性带约束公式,寻找最小的www仍有困难,考虑将其转化为一个近似的公式,通过寻找公式中最小的www,达到寻找原公式最小www的目的,利用泰勒展开。
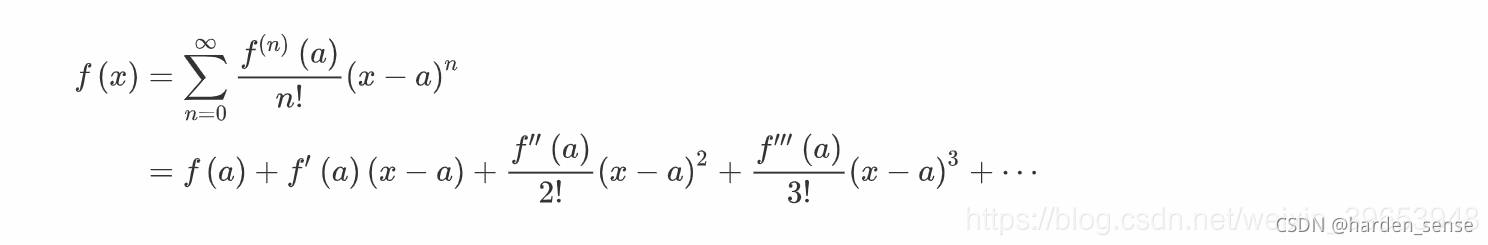
我们将EinE_{in}Ein在wtw_twt处展开≈Ein(wt)+(wt+ηv−wt)+ΔEin(wt)\approx{E_{in}}(w_t)+(w_t+\eta{v}-w_t)+\Delta{E_{in}(w_t)}≈Ein(wt)+(wt+ηv−wt)+ΔEin(wt)
进一步转化为:
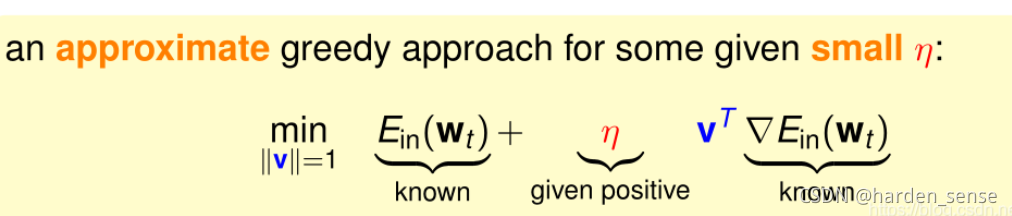
迭代的目的是让Ein(wt)E_{in}(w_t)Ein(wt)越来越小,即让Ein(wt+ηv)<Ein(wt)E_{in}(w_t+\eta{v})<E_{in}(w_t)Ein(wt+ηv)<Ein(wt)
η\etaη为标量,如果两个向量方向相反,则他们的内积最小为负。也就是说更新方向和梯度方向相反的话,就能保证每次迭代Ein(wt+ηv)<Ein(wt)E_{in}(w_t+\eta{v})<E_{in}(w_t)Ein(wt+ηv)<Ein(wt) 。于是令梯度下降方向为:

vvv是单位向量,每次都沿着梯度的反向更新,这种算法称为:梯度下降,实际应用中最常用的为随机梯度下降。
更新方向确定后,再来看步长对下降的影响:
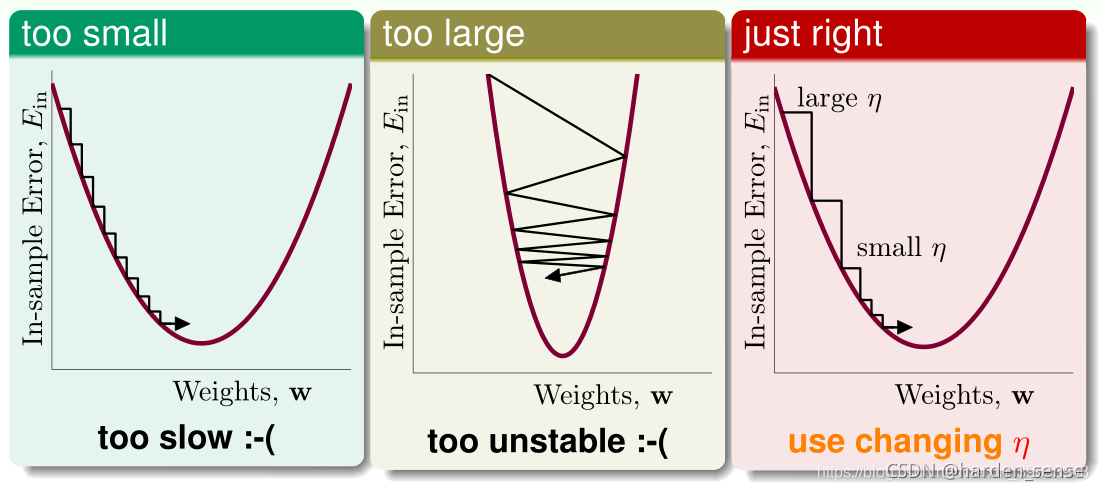
步长太小的话 下降速度过慢,步长过大又容易反复横跳。因此选取合适的步长就非常的重要:这里给出步长计算公式:

最终的计算公式为:

此时的η\etaη称为固定学习率,公式称为固定学习率的梯度下降
总结以下梯度下降的算法的流程:

- 初始化权重:初始化权重向量www为w0w_0w0
- 计算梯度:ΔEin(wt)\Delta{E_{in}(w_t)}ΔEin(wt)
- 迭代更新
- 计算终止:ΔEin(wt)\Delta{E_{in}(w_t)}ΔEin(wt)=0迭代结束
 逻辑回归与梯度下降在二元分类中的应用
逻辑回归与梯度下降在二元分类中的应用





















 3511
3511

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








