机器学习：噪声和错误

噪声和错误

我们之前的研究都是假设在样本数据完美，没有噪声存在的前提下进行推导的。然后得出机器能够学到东西的结论，但是，现实中噪声的存在是不可避免的。所谓的噪声就是样本中有问题的点。以银行卡发放的列子，来阐述噪声产生的原因：

• 样本标记错误。比如说应该发放银行卡的用户，错误的标记为不符合规定的用户。
• 不同的评判标准，导致噪声的产生。比如两个用户的属性状态基本一致，判定一个发放另一个不发放。
• 输入样本中存在噪声。也就是用户的信息输入有错误。来看一下有噪声的机器学习流程图：
  
  那么存在噪声时机器学习还能有效果吗？VC限制还能起到作用吗？
  再看关于小球的列子，没有噪声的时候，输入样本和整体样本服从同一概率分布，不论是罐子中的小球数目还是抽样取出的小球。这种情况下使用的是确定性的小球，其中小球的颜色类比目标函数和假设函数是否一致。标记取决于目标函数，这种学习方法叫做判别学习法。在现实中，数据中多含有噪声，数据基本上还是服从同一概率分布，但是小球的颜色并不固定，可以想象为小球的颜色在不停的发生变化。只能在拿出小球的那一刻才能确定他的颜色，这种小球把他称为概率性小球。对应到机器学习上就是含有噪声的样本，也就是$y\ne h(x)$并不确定，其中标记$y$服从概率分布$P(y|X)$,这一形式称为目标分布，来看一个简单的列子：
  $$P(+1|x)=0.7$$ $$P(-1|x)=0.3$$
  则一定选择错误率小的目标，根据这个原则，这个标记目标记为+1，而30%为-1是噪声。目标函数分布是一个特殊分布，符合下面的式子：$$P(+1|x)=1⟺y=f(x)$$
  $$P(+1|x)=1⟺y\ne f(x)$$

因此，有两个分布函数$P(X)和P(y|X)$，其中$P(X)$越大，意味着$X$被选为样本的概率越大；$P(y|X)$越大意味着该样本是某一类的概率越大，两者结合起来，在常见的样本点上的分类尽量正确。

这样得出，VC限制仍然适用，因为这种含有噪声的输入样本以及标记分别服从$P(X)和P(x|Y)$，即服从$P(X,y)$的联合概率分布。

接下来对机器学习的流程图做出相应的修改：

1.错误的测量

我们一直在做的事情就是，让我们找出的假设函数g和真实的目标函数$f(x)$尽可能的接近，接近就意味着更少的犯错误。衡量错误的方式主要考虑了以下三个因素：

• 样本外的未知数据：所有样本x的平均

• 逐点估计：每个数据点单独评估

• 分类估计：看目标和预测是否一致，二元分类通常只有两个类别，相同为1不同为0，通常称为0/1error
  
  可以用$err()$函数表示逐点的错误衡量。因此训练样本和整个样本空间的错误衡量可以用下面的式子进行表示：
  
  为了方便述，将假设函数$g(x)$表示为$\tilde{y}$，目标函数表示为$y$。

  除了常用在分类（classification）上的 0/1误差衡量之外，还有用在回归（regression）上的平方误差（square error）衡量，它也是一种逐点（pointwise）的错误衡量方式，如下式所示。
  

错误衡量对机器学习有着指导作用。

在含有噪音的情况下，目标分布函数 $P(X\mid y)$和逐点误差函数$err()$ 共同决定了理想的错误率最小目标函数（ideal mini-target）f。

接下来看一个列子，以便更好的理解错误衡量

假使三个目标分布函数$P(y|X)$，分别在计算0/1错误衡量和平方错误衡量下的标记错误率。 如下图所示：左图很容易就能就能得出。右图中目标函数$f(x)$的平均值为：$f(x)=\sum y\cdot P(y\mid X)=1\times 0.2+2\times 0.7+3\times 0.1=1.9$预测标签1的均方误差为$(1-1)2\times 0.2+(2-1)2\times 0.7+(4-1)2\times 0.1=1.1$

至此在上一节的基础上对机器学习流图做了进一步的修改，如图8-5所示，加入了错误衡量的模块，该模块对算法和最终的假设选择都起着很大影响。

在此基础上，修正机器学习算法的流程图，加入错误衡量模块，该模块对算法和最终假设起到了关键作用。

2.算法的错误衡量

二元分类问题的错误类型也分为两类，如下图所示：

错误拒绝：目标函数为+1，假设函数给出了-1
错误接受：目标函数为-1，假设函数给出了+1

这两种错误造成的损失是不同的。

举两个常见的例子，在超市给年消费额高的会员发放赠品时，如果出现了错误的接受，即该会员没有资格领取到赠品，超市依旧给他发放了赠品，该损失只是超市多发了一些赠品；但若错误的拒绝，意味着该会员有资格领取到赠品，超市却拒绝给他发放，损失的不只是超市的信誉，还可能会造成客户流失。

另一个例子是在安全部门中，员工有查看资料的权限，系统却拒绝了他的请求，这是一种错误的拒绝，员工最多也就是抱怨一下；但若一个员工没有查看资料的权限，系统却同意了，这是一种错误的接受，损失可能会非常大，甚至有可能威胁到国家的利益。这两种情况的损失可能如图所示。

在不同的应用中应该给出不同的错误衡量方式。在设计算法时，最好依据各种错误的损失情况来设计损失函数，现在的问题就是错误损失函数得值如何确定。在设计算法时，通常采用代替的方式来进行设计：

• 合理的：在分类错误衡量中，可以想象这种噪音的情况相对于整体一定是小的，因此只需要找到一个足够小的错误即可；在平方错误衡量中，只要认同噪音服从高斯分布，减小高斯中平方项，就如同在减少平方错误。将这种近似的错误衡量方式用$\widetilde{err}$表示。
  友善的：很容易设计一种算法A。如寻找最小的0/1错误是一个NP-HARD问题，而实际中设计算法时，运用错误率比前者更小的原则，即寻找越来越小的错误率。以后的章节中会提到两种方式：直接求出结果（closed-form solution）；凸求解方程（convex objective function）。

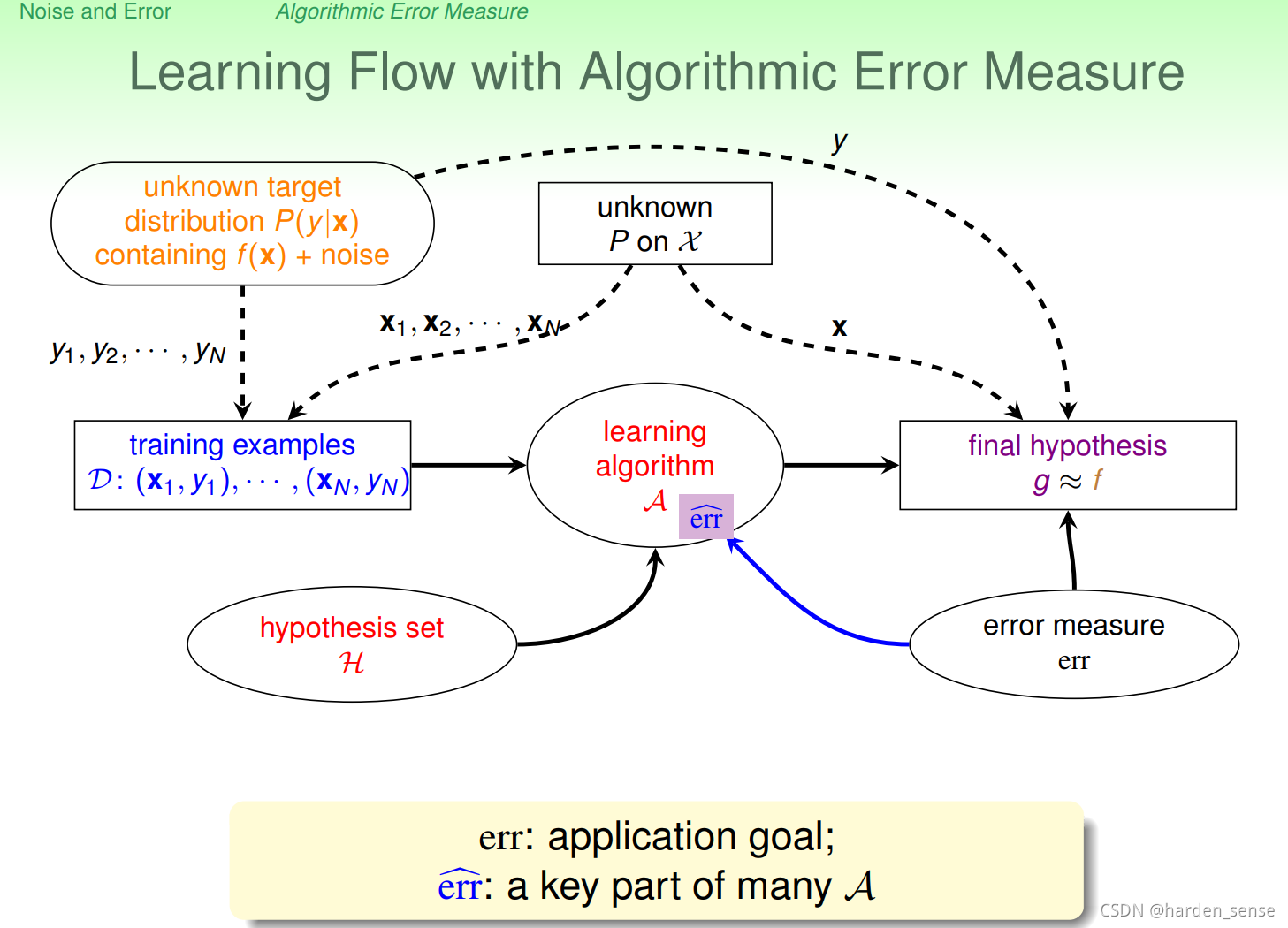
进一步修正我们的机器学习流程图。

3.权重分类

出现错误的方式，如下图这个列子，我们称这样的错误方式为：成本矩阵，或者误差矩阵等。

使用上面的矩阵表示，可以写为下面这种形式：

因为VC的限制，我们可以保证整体的错误近似接近样本空间上的错误，因此只需要让样本空间上的错误尽可能接近于0就行，但是这里的错误和之前的不加区分的错误是有差别的。我们用加权错误来表示。$E_{in}^w(h)$

假设存在线性不可分的情况，我们用pocket算法进行分类，一定会产生错误。大部分算法和PLA一致，如果$W_{t+1}$产生的代价函数$E_{in}^w(h)$比$W$来的小，我们就用现在的这个来代替之前的。pocket算法的代价函数该怎么进行定义，是我们关心的问题。有一种思路是对D中的样本进行复制：

将一个样本复制1000份，比如$(x_1,+1)$,当该样本点犯错误时，错误就被累加了1000次。同样该样本点出现的概率也增大了1000倍。