机器学习：线性回归

最新推荐文章于 2024-09-20 15:11:17 发布

harden_sense

最新推荐文章于 2024-09-20 15:11:17 发布

阅读量749

点赞数

分类专栏：机器学习文章标签：机器学习线性回归回归

本文链接：https://blog.youkuaiyun.com/jiaolong123456/article/details/121246029

版权

机器学习专栏收录该内容

13 篇文章

订阅专栏

本文深入探讨了线性回归与线性分类的区别，重点介绍了线性回归的原理和最小二乘法求解过程。线性回归通过最小化误差来确定最佳权重，而线性分类则涉及NP-hard问题。尽管两者输出空间不同，但线性回归的误差衡量方法在某些情况下也可应用于线性分类。此外，文章还讨论了线性回归的泛化能力和几何意义。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

线性回归

之前介绍的信用卡发放列子，我们从数据集出发进行训练，最后得出的结论是：给或者不给，输出空间为{+1,-1}。但是，我们想要从这些数据出发，最后让机器告诉我们给他们多大的额度是最合适的，输出空间为 $R^+$ 。这就是不同于之前提到的Linear Classification的Linear Regression线性回归问题。二者的对比我们可以从下图中进行区分：
在这里插入图片描述
还是以信用卡为列，输入空间和之前的相同，如年龄、性别、月收入等等。也即 $X=[x_0,x_1,x_2.......x_d]$ 特征空间为 $d + 1$ 维，其中第一个维度是维常数项，因为输出空间的变化，导致假设函数和二元分类略有不同，但基本思想相差不大。仍然需要考虑每个分量的不同加权，然后求和。最终得出结果。唯一不同的是最终结果不需要 $s i g n ()$ 函数的作用。
在这里插入图片描述
所谓的线性回归本质上就是：根据训练样本的数据，画出一条线。类似于已知函数的点，求出函数的解析式。然后根据这个解析式，可以求出任意点的对应的函数值。线性回归的任务就是找到这个函数的解析式，然后在预测某一个点对应值，可能会有少许的误差。如下图所示：
在这里插入图片描述
蓝色的线为我们根据训练集画出的预测函数，圈圈是真实的数据点，二者可能会存在一定的偏差。线性回归的演算法要做的事情是：让误差最小。最常用的误差衡量方式是基于最小二乘法的思想，其目标是计算最小误差，和对应权重 $w$ 。误差的计算形式为最小均方误差：
在这里插入图片描述
在这个问题中假设函数 $h$ 对应于权重和特征的乘积，如上图（9-5）所示可以将 $h$ 进行变形。这里使用的数据集是含有误差的，因此 $(X, y)$ 服从联合概率分布。

1.最小化误差

有了 $E_{in}(w)$ 的计算方式，现在要考虑的问题就是将误差最小化，在误差最小化之前先对误差的衡量公式进行一个变形，用矩阵的形式来表示：
在这里插入图片描述
（X,y）都是已知数据，所以目标就转化为，寻找 $w$ 使误差最小，在此之前我们先考虑一维的情况。很明显图像为一个开口向上的抛物线

显然该函数在一维的情况下是一个凸函数，可微，连续。该函数存在最小值，最小值点在导数为0时取得。在X是多维的时候仍然满足凸函数的条件，由此我们可以得到：
在这里插入图片描述
接下来需要寻找一个 $W$ 让误差的微分为0，在此之前先对上面推导出来的公式进行简单变形得到如下形式：

然后对该式子进行求导：

具体利用的为矩阵求导的内容，关于矩阵求导，可以参考知乎的文章https://zhuanlan.zhihu.com/p/273729929。然后将一些值代入：

在这里插入图片描述令上式为0可以得出如下结论：

用 $X^+$ 来代替 $X^TX)^{-1}X^T$ 可以简化为右图所示的形式。其中 $X^+$ 表示矩阵的 $X$ 的违逆。矩阵X只有当 $N = d + 1$ 才是方阵，伪逆矩阵和逆矩阵有很多相似之处。 $X^TX$ 在大部分情况下是可逆的，原因是在机器学习中，样本数量远远大于特征向量的维数。因此在 $X^TX$ 存在足够的自由度满足可逆的条件。如果该矩阵不可逆，说明最佳的 $W$ 有很多个，只需要找到一个满足条件的即可。

线性回归的算法求解如下：

首先通过已知的数据集 $X$ ,构建输入矩阵 $X$ 与输出向量y的标签：
然后构造输入矩阵和输出向量，求解伪逆
最后通过伪逆求出假设函数

2.泛化问题

上面的方法是否为机器学习？或者说该方法是否具有很好的泛化能力。
在这里插入图片描述
回答不是的理由：求解只需要一步就完成，不想像前面的算法，都是经过了很多步的。用该方法好像就是，我们只要有数据集自己完全可以根据公式进行计算，得出最佳的假设函数。好像机器学习并没有什么用处。

回答是的理由：更看重结果，这种直接求解方式是数学推导中的精确解，因此求出的W一定是让误差最小的解，而且求解伪逆的方法也是需要经过不同的迭代才能完成，并非我们看到的那样直接得出结果。而怕判断机器学习最主要的标准是学习到的 $E_{out}$ 是否足够好。

通过改进VC-bound，也可以证明在线性回归问题中VC起到了很好的约束作用，即找到了好的 $E_{in}(w)$ 就可以保证 $E_{out}(w)$ 足够的好。下面通过一种更简单的方法，证明线性回归问题是可以通过线下最小二乘法方法计算得到好的 $E_{in}(w)$ 和 $E_{out}(w)$ 。
在这里插入图片描述

通过几何图形更具体的了解 $H$ 矩阵的物理含义：

可以这样理解：如果不存在噪声，我们得到的是y向粉色空间的投影，该投影就是预测值，有了噪声的存在我们得到的预测值就是 $f (x)$ 粉色空间里面的那条红线。
在这里插入图片描述

3.线性回归的误差衡量用到线性分类

线性分类问题使用误差衡量方法是0/1 error，那么线性回归的平法误差能否应用到线性分类问题呢？

首先对比二元线性分类与线性回归之间的差异，分别在三个部分进行对比，输出空间、假设函数和错误衡量函数，如图所示。

在这里插入图片描述
从求解问题的难度考虑，二元分类的求解是一个NP-hard问题，只能使用近似求解的方式，而线性回归通过求解析解，求解方便，程序编写也简单。

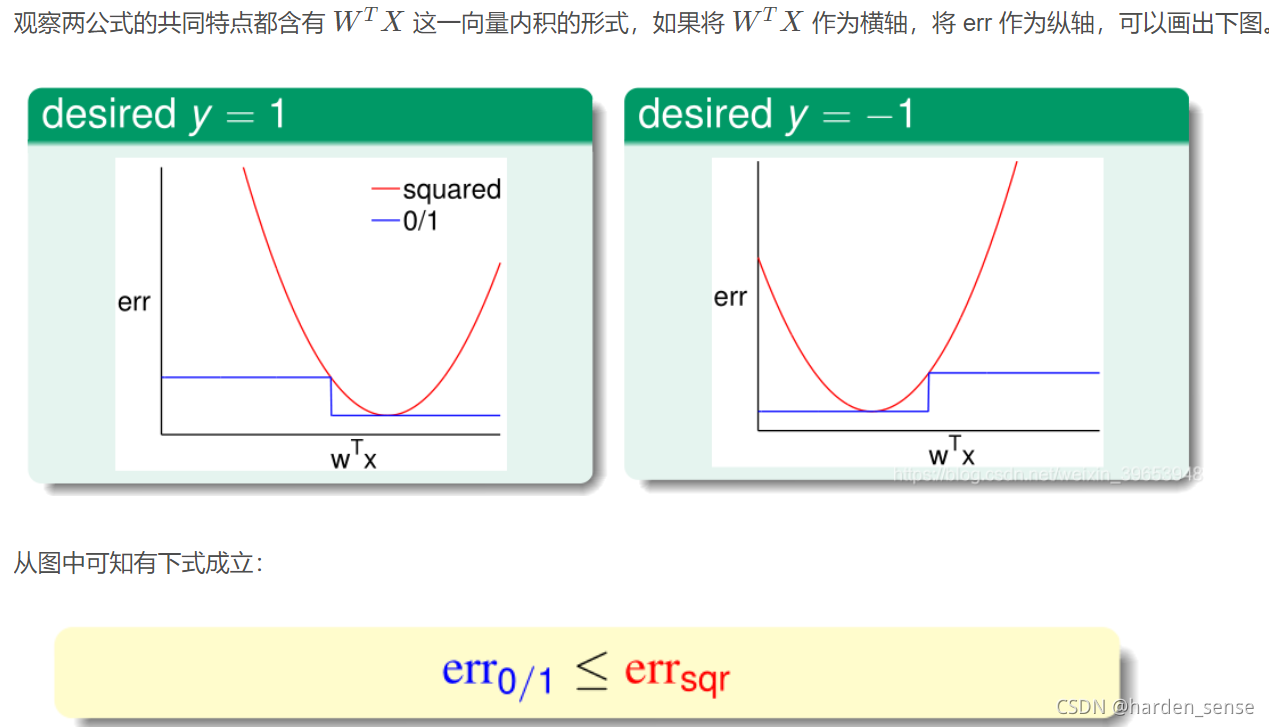
因此考虑能否通过求解线性回归的方式求二元分类问题，因为二元分类的输出空间 ${ − 1 ， + 1 }$ 属于线性回归的输出空间，即 ${ − 1 ， + 1 } ∈ R$ ，其中数据集的标记大于零的表示+1，小于零的表示-1，通过线性回归求得的解析解 $W_{ L I N}$ ，直接得出最优假设 $g ( X ) = s i g n ( W_{ L I N }X)$ 但是这种推理只符合直觉，而如何使用数学知识去说明这种方式的合理性呢？
在这里插入图片描述

参考：
https://www.cnblogs.com/ymingjingr/p/4306666.html
https://github.com/RedstoneWill/HsuanTienLin_MachineLearning
https://blog.youkuaiyun.com/weixin_39653948/article/details/105547804