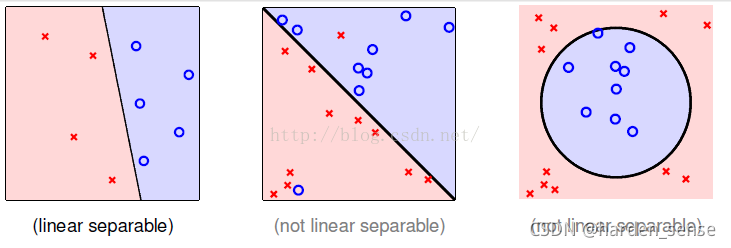
感知机算法(PLA)主要用于解决线性可分问题。如果给定的数据集是线性可分得,PLA可以找到一条很好的线在高维空间的表现就是超平面,把数据集完美的进行划分。
训练完成之后,在给出新的数据,PLA可以很好的预测。
用一个简单的列子加以说明,银行决定是否给某人信用卡。银行有客户的一些资料,比如他的年龄,教育程度,工资水平就等等特征信息。我们把这些信息记为向量X。X={年龄,工资,教育程度等等}。是否给他信用卡用y表示,给他信用卡记为+1,不给记为-1。每一个特征都占据不同的比重,比如年龄的影响较小,我们给的比重小一点,工资的影响较大,我们给工资的比重就适当的大一点。我们把各个特征的比重信息记作W。
当每一个特征,与对应比重的乘积大于某个阈值,我们就给信用卡,否则就不给。如下所示:
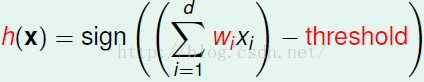
我们将阈值加入到特征向量X中,并且给他的特征值记为1
可与i将公式进行简化:
h(x)=sign((∑i=0dwixi))h(x)=sign((\sum_{i=0}^{d}w_ix_i))h(x)=sign((i=0∑dwixi))
用向量的乘法进行表示:
这个算法的关键问题就在家于确定w的值,我们的思路是这样的,先给定一个初始的w,然后将样本点带入计算,如果计算出的结果,与给定的结果相同,保持w的值不变继续进行下一个样本点的验证。当出现不一致时,也即我们计算的结果和给定的结果不一样,对w的值进行修正。 具体修正的策略如下所示:
分为两种情况:
- 样本点为+1。我们计算的结果却是-1.说明w和X的夹角过大,我们需要让夹角变得小一点:
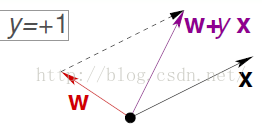
wt+1=wt+xiyiw_{t+1} =w_t+x_iy_iwt+1=wt+xiyi- 同样的分析方法,得到另一种错误的更新方式:
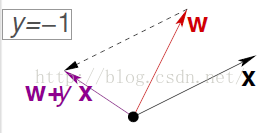
wt+1=wt+xiyiw_{t+1} =w_t+x_iy_iwt+1=wt+xiyi
因为此时的xiyix_iy_ixiyi为一个负值,相当于做了一个向量减法,夹角增大。
更新w的方法我们已经有了,接下来我们要思考的问题是:每次更新之后的wt+1w_{t+1}wt+1所得的效果是否比wtw_twt的效果更好。在回答这个问题之前我们先假设,存在一个完美的
wfw_fwf能够将样本点完美的进行划分。

上述结果表明,wt+1w_{t+1}wt+1比之前的wtw_twt,更接近wfw_fwf。
另一个比较重要的问题是,该算法能否停下来的问题。

上述结果告诉我们,wt+1w_{t+1}wt+1的增加量有一个上限,wfw_fwf和wt+1w_{t+1}wt+1之间的夹角值不超过1,所以一定能够收敛。具体次数也可以通过计算得出。

对于线性不可分的数据也可以使用,采用的是贪心算法。具体不做介绍。





 本文介绍了感知机算法(PLA)的基本原理及应用。PLA主要用于解决线性可分问题,如银行决定是否发放信用卡等场景。文章详细解释了如何通过调整权重向量来优化分类效果,并讨论了算法的收敛性。
本文介绍了感知机算法(PLA)的基本原理及应用。PLA主要用于解决线性可分问题,如银行决定是否发放信用卡等场景。文章详细解释了如何通过调整权重向量来优化分类效果,并讨论了算法的收敛性。
















 5297
5297

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








