Java算法(01) -- 如何判断链表有环

1、题目分析

有一个单向链表，链表中有可能出现“环”，就像下图这样。如何用程序来判断该链表是否为有环链表呢？

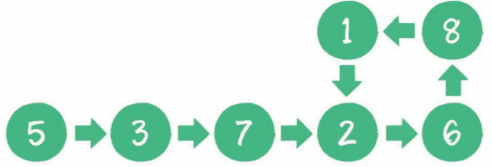
方法一

方法流程：

• 从头节点开始，依次遍历单链表中的每一个节点；
• 每遍历一个新节点，就从头检查新节点之前的所有节点，用新节点和此节点之前所有节点依次做比较；
• 如果发现新节点和之前的某个节点相同，则说明该节点被遍历过两次，链表有环；
• 如果之前的所有节点中不存在与新节点相同的节点，就继续遍历下一个新节点，继续重复上述的操作

具体流程：

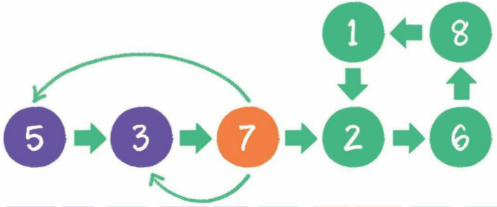
• 如上图，当遍历链表节点7时，从头访问节点5和节点3，发现已遍历的节点中并不存在节点7，则继续往下遍历；
• 当第2次遍历到节点2时，从头访问曾经遍历过的节点，发现已经遍历过节点2， 说明链表有环；

【假设链表的节点数量为n，则该解法的时间复杂度为O(n²)；由于并没有创建额外的存储空间，所以空间复杂度为O(1)】

方法二

方法流程：

• 创建一个以节点ID为Key的HashSet集合，用来存储曾经遍历过的节点；
• 从头节点开始，依次遍历单链表中的每一个节点，每遍历一个新节点，都用新节点和HashSet集合中存储的节点进行比较；
• 如果发现HashSet中存在与之相同的节点ID，则说明链表有环；
• 如果HashSet中不存在与新节点相同的节点ID，就把这个新节点ID存入HashSet中，之后进入下一节点，继续重复刚才的操作

具体流程：

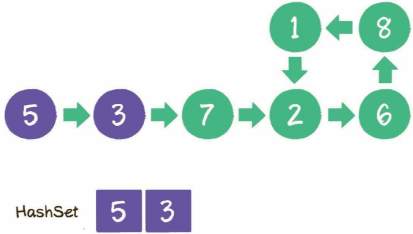
• 遍历过5、3，如下图：
  
• 遍历过5、3、7、2、6、8、1，如下图：
  
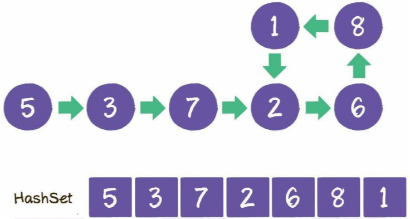
• 当再一次遍历节点2时，查找HashSet，发现节点已存在
  
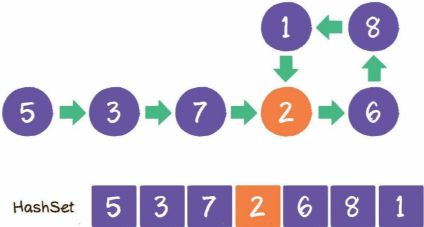
  由此可知，链表有环；这个方法在流程上和方法1类似，本质的区别是使用了HashSet作为额外的缓存。
  【假设链表的节点数量为n，则该解法的时间复杂度是O(n)；由于使用了额外的存储空间，所以算法的空间复杂度同样是O(n)】

方法三【双指针】

方法流程：

• 创建两个指针p1和p2（在Java里就是两个对象引用），让它们同时指向这 个链表的头节点；