图解排序算法(03) -- 彻底搞懂快速排序

1、初识快速排序

同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换位置来达到排序的目的。
不同的是：

• 冒泡排序在每一轮中只把1个元素冒泡到数列的一端
• 快速排序则在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成两个部分；这种思路就叫作分治法，如下图所示：
  

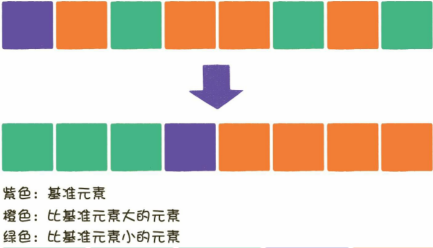
使用分治法的优势

假如给出一个8个元素的数列，一般情况下，使用冒泡排序需要比较7轮，每一 轮把1个元素移动到数列的一端，时间复杂度是O(n²)；快速排序的流程如下：
【原数列在每一轮都被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止】

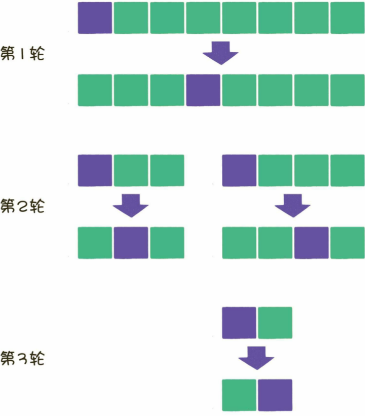
每一轮的比较和交换，需要把数组全部元素都遍历一遍，时间复杂度是O(n)；
假如元素个数是n，那么平均情况下需要遍历logn轮，因此快速排序算法总体的平均时间复杂度是O(nlogn)

2、基准元素的选择

在分治过程中，以基准元素为中心，把其他元素移动到它的左右两边；
选择基准元素最简单的方式是选择数列的第1个元素，如下图：

例外：假如有一个原本逆序的数列，期望排序成顺序数列，如下图：

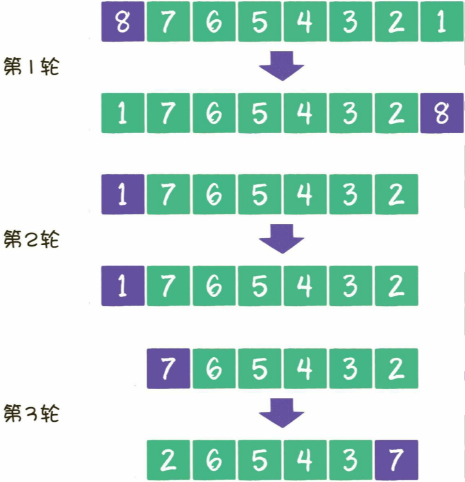
【整个数列并没有被分成两半，每一轮都只确定了基准元素的位置，在这种情况下，数列的第1个元素要么是最小值，
要么是最大值，根本无法发挥分治法的优势，快速排序需要进行n轮，时间复杂度退化成了O(n²)】

避免上面这种情况，可以随机选择一个元素作为基准元素，并且让基准元素和数列首元素交换位置

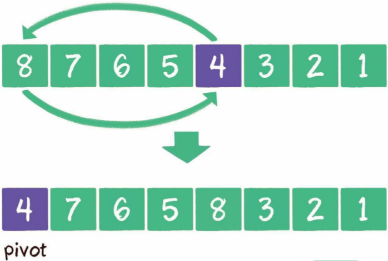
通过上述方法，可以有效地将数列分成两部分，但即使随机选择基准元素，也会有极小的几率选到数列的最大值或最小 值，同样会影响分治的效果；所以，快速排序的平均时间复杂度是O(nlogn)，但最坏情况下的时间复杂度O(n²)
【在后文中，直接将首元素作为基准元素】

3、元素的交换

选定了基准元素之后要进行元素的交换，即把其他元素中小于基准元素的都交换到基准元素一边，大于基准元素的都交换到基准元素另一边，实现有两种方法：双边循环法和单边循环法

双边循环法(递归)

给出原始数列如下，要求对其从小到大进行排序

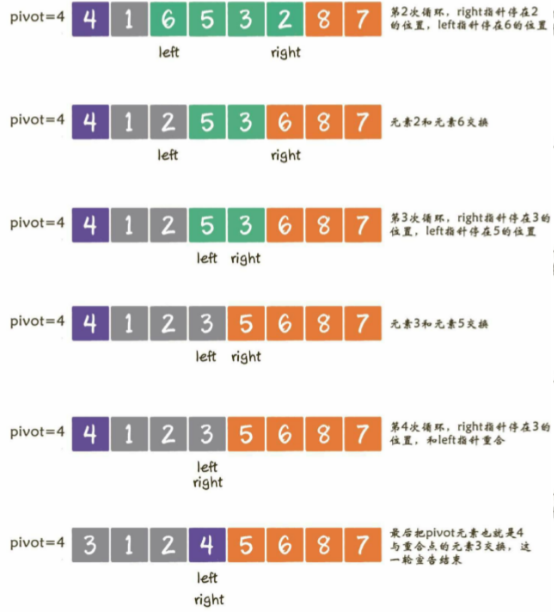
1、选定基准元素pivot，并且设置两个指针left和right，指向数列的最左和最右两个元素

2、进行第1次循环，从right指针开始，让指针所指向的元素和基准元素做比较【如果大于或等于pivot，则指针向左移动；如果小于pivot，则right指针停止移动，切换到left指针】；
在当前数列中1<4，所以right直接停止移动，换到left指针；让指针所指向的元素和基准元素做比较【如果小于或等于 pivot，则指针向右移动；如果大于pivot，则left指针停止移动】；
由于left开始指向的是基准元素，判断肯定相等，所以left右移1位，如下图：

由于7>4，left指针在元素7的位置停下；这时让left和right指针所指向的元素进行交换

3、进入第2次循环，重新切换到right指针，向左移动；right指针先移动到8，8>4，继续左移；由于2<4，停止在2的位置，后续步骤如下图所示：

双边循环法代码实现

Code:【使用递归】

import java.util.Arrays;

/**
 * @ClassName QuickSort
 * @Description  快速排序
 * @Date: 2020/3/28
 * @Version 1.0
 */
public class QuickSort {
    public static void quickSort(int[] arr,int startIndex,int endIndex){
    //递归结束条件：startIndex >=  endIndex
        if(startIndex >= endIndex){
            return;
        }
    // 获取基准元素
        int pivotIndex = partiton(arr,startIndex,endIndex);
    // 根据基准元素，分成两部分进行递归排序
    quickSort(arr,startIndex,pivotIndex -1);
    quickSort(arr,pivotIndex + 1,endIndex);
    }

    //双边循环法
    //arr 带交换的数组
    //startIndex 起始下标
    //endIndex  结束下标
    public static int partiton(int[] arr,int startIndex,int endIndex){
       //取第一个位置(也可以随机)的元素为基准元素
       int pivot = arr[startIndex];
       int left = startIndex;
       int right = endIndex;

       while (left != right){
           //控制right指针比较并左移
           while (left<right && arr[right]>pivot){
               right--;
           }
           //控制left指针比较并右移
           while (left < right && arr[left] <= pivot){
               left++;
           }
           //交换left和right指针所指向的元素
           if(left < right){
               int p = arr[left];
               arr[left] = arr[right];
               arr[right] = p;
           }
       }

       //pivot和指针重合点交换
        arr[startIndex] = arr[left];
        arr[left] = pivot;
        return  left;
    }

    public static void main(String [] args){
        int[] arr = new int[]{4,7,6,5,3,2,8,1};
        System.out.println("排序前：" + Arrays.toString(arr));
        quickSort(arr,0,arr.length-1);
        System.out.println("排序后：" + Arrays.toString(arr));
    }
}

编译输出：【partition方法则实现了元素的交换，让数列中的元素依据自身大小分别交换到基准元素的左右两边】

单边循环法（递归）

双边循环法从数组的两边交替遍历元素，虽然更加直观，但是代码实现相对烦琐；
单边循环法只从数组的一边对元素进行遍历和交换，较为简单，详细过程：
给出原始数列如下，要求对其从小到大进行排序：

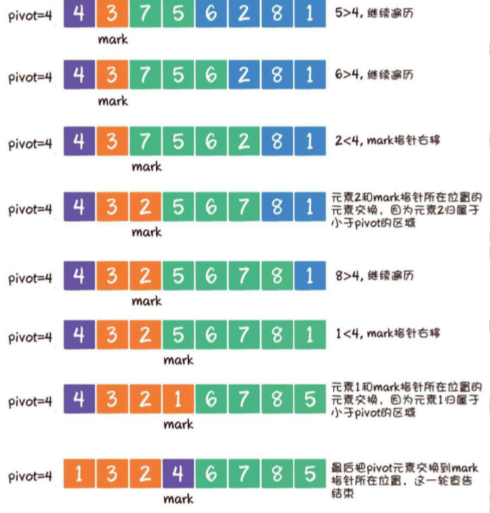
1、选定基准元素pivot，同时设置一个mark指针指向数列起始位置，这个mark指针代表小于基准元素的区域边界

2、从基准元素的下一个位置开始遍历数组

• 如果遍历到的元素大于基准元素，续往后遍历；
• 如果遍历到的元素小于基准元素，则需要做两件事：
• 1、把mark指针右移1 位，因为小于pivot的区域边界增大了1；
• 2、让最新遍历到的元素和mark指针所在位置的元素交换位置，【因为最新遍历的元素归属于小于pivot的区域】

遍历到元素7，7>4，所以继续遍历

来遍历到的元素是3，3<4，所以mark指针右移1位

让元素3和mark指针所在位置的元素交换，因为元素3归属于小于pivot 的区域

3、继续遍历，后续步骤如图所示：

单边循环法代码实现

Code:【使用递归】

/**
 * @ClassName QuickSort
 * @Description  快速排序
 * @Date: 2020/3/28
 * @Version 1.0
 */
public class QuickSort2 {
    public static void quickSort(int[] arr,int startIndex,int endIndex){
    //递归结束条件：startIndex >=  endIndex
        if(startIndex >= endIndex){
            return;
        }
    // 获取基准元素
        int pivotIndex = partiton(arr,startIndex,endIndex);
    // 根据基准元素，分成两部分进行递归排序
    quickSort(arr,startIndex,pivotIndex -1);
    quickSort(arr,pivotIndex + 1,endIndex);
    }

    //单边循环法
    //arr 带交换的数组
    //startIndex 起始下标
    //endIndex  结束下标
    public static int partiton(int[] arr,int startIndex,int endIndex){
       //取第一个位置(也可以随机)的元素为基准元素
       int pivot = arr[startIndex];
       int mark = startIndex;
       for(int i = startIndex+1;i<endIndex;i++){
           if(arr[i]<pivot){
               mark++;
               int p = arr[mark];
               arr[mark] = arr[i];
               arr[i] = p;
           }
       }
        arr[startIndex] = arr[mark];
        arr[mark] = pivot;
        return  mark;
    }

    public static void main(String [] args){
        int[] arr = new int[]{4,7,6,5,3,2,8,1};
        System.out.println("排序前：" + Arrays.toString(arr));
        quickSort(arr,0,arr.length-1);
        System.out.println("排序后：" + Arrays.toString(arr));
    }
}

编译输出：【partition方法则实现了元素的交换，让数列中的元素依据自身大小分别交换到基准元素的左右两边】

非递归实现

绝大多数的递归逻辑，都可以用栈的方式来代替
代码中一层一层的方法调用，本身就使用了一个方法调用栈；
【每次进入一个新方法，就相当于入栈；每次有方法返回，就相当于出栈】
所以，可以把原本的递归实现转化成一个栈的实现，在栈中存储每一次方法调用的参数。

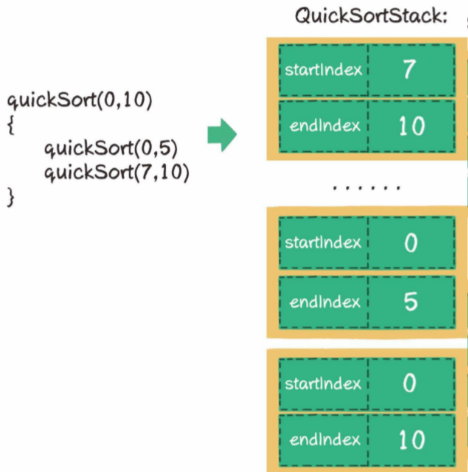
非递归代码实现

Code:【非递归】

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;

/**
 * @ClassName QuickSort
 * @Description  快速排序
 * @Date: 2020/3/28
 * @Version 1.0
 */
public class QuickSort3 {
    public static void quickSort(int[] arr,int startIndex,int endIndex){
    //用一个集合栈来代替递归的函数栈
    Stack<Map<String,Integer>> quickSortStack = new Stack<Map<String,Integer>>();
    // 整个数列的起止下标，以哈希的形式入栈
        Map rootParam = new HashMap();
        rootParam.put("startIndex",startIndex);
        rootParam.put("endIndex",endIndex);
        quickSortStack.push(rootParam);

    // 循环结束条件：栈为空
    while (!quickSortStack.isEmpty()){
        //栈顶元素出栈，得到起止下标
        Map<String,Integer> param = quickSortStack.pop();
        //得到基准元素位置
        int pivotIndex = partiton(arr,param.get("startIndex"),param.get("endIndex"));
        //根据基准元素分成两部分，把每一部分的起止下标入栈
        if(param.get("startIndex")< (pivotIndex -1)){
            Map<String,Integer> leftParam = new HashMap<String, Integer>();
            leftParam.put("startIndex",param.get("startIndex"));
            leftParam.put("endIndex",pivotIndex-1);
            quickSortStack.push(leftParam);
        }
        if(pivotIndex + 1 < param.get("endIndex")){
            Map<String,Integer> rightParam = new HashMap<String, Integer>();
            rightParam.put("startIndex",pivotIndex+1);
            rightParam.put("endIndex",param.get("endIndex"));
            quickSortStack.push(rightParam);
        }
    }
 }

    //单边循环法
    //arr 带交换的数组
    //startIndex 起始下标
    //endIndex  结束下标
    public static int partiton(int[] arr,int startIndex,int endIndex){
        //取第一个位置(也可以随机)的元素为基准元素
        int pivot = arr[startIndex];
        int mark = startIndex;
        for(int i = startIndex+1;i<= endIndex;i++){
            if(arr[i]<pivot){
                mark++;
                int p = arr[mark];
                arr[mark] = arr[i];
                arr[i] = p;
            }
        }
        arr[startIndex] = arr[mark];
        arr[mark] = pivot;
        return  mark;
    }

    public static void main(String [] args){
        int[] arr = new int[]{4,7,6,5,3,2,8,1};
        System.out.println("排序前：" + Arrays.toString(arr));
        quickSort(arr,0,arr.length-1);
        System.out.println("排序后：" + Arrays.toString(arr));
    }
}

编译输出：【非递归方式代码的变动只发生在quickSort方法中； 该方法引入了一个存储Map类型元素的栈，用于存储每一次交换时的起始下标和结束下标。
**每一次循环，都会让栈顶元素出栈，通过partition方法进行分治，并且按照 基准元素的位置分成左右两部分，左右两部分再分别入栈，**当栈为空时，说明排序 已经完毕，退出循环】
———————————————————————————————————————
内容来源：《漫画算法》
关注公众号，回复 【算法】，获取高清算法书！