图论06-【无权无向】-图的遍历并查集Union Find-力扣695为例

最新推荐文章于 2025-12-06 21:22:01 发布

原创最新推荐文章于 2025-12-06 21:22:01 发布 · 1.2k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#图论 #leetcode #算法

图论专栏收录该内容

19 篇文章

订阅专栏

文章介绍了如何使用并查集数据结构解决二维网格中最大岛屿面积问题，包括UF变量设计、合并两个集合的方法以及find和unionElements函数的实现。

文章目录

1. 代码仓库
2. 思路
3. 完整代码

1. 代码仓库

https://github.com/Chufeng-Jiang/Graph-Theory

2. 思路

2.1 UF变量设计

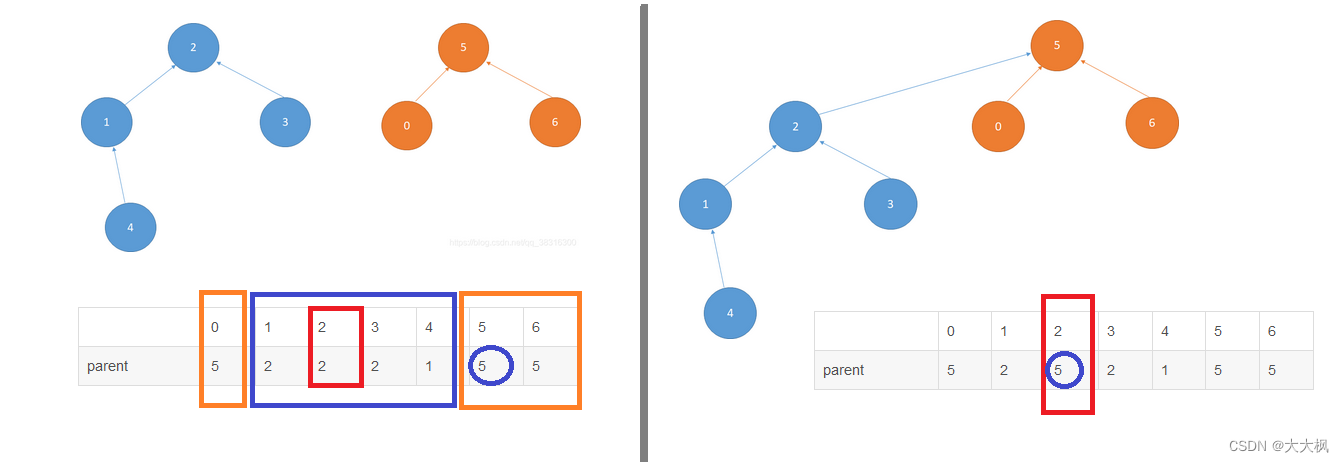
在这里插入图片描述

parent数组保存着每个节点所指向的父节点的索引，初始值为当前顶点编号，指向自己。

后期在合并的时候均指向其合并的另一个元素的父节点，也就是p->a, q->q,合并p和q时，改变q的指向，q->a.

最终a下面挂两个节点，分别为p, q.

//parent数组中保存着每个节点所指向的父节点的索引
private int[] parent;

sz数组来保存每个根节点所代表的子树中元素的数量 
private int[] sz;

2.2 UF合并两个集合

查找两个元素的父节点，父节点相同则属于同一个集合

public void unionElements(int p, int q) {

    int pRoot = find(p); // 找到p的父节点
    int qRoot = find(q); // 找到q的父节点

    if (pRoot == qRoot) // 如果pq的父节点相同，说明在同一个集合内
        return;

    parent[pRoot] = qRoot; //如果不相同，将p的父节点挂到q的父节点下，进行合并
    sz[qRoot] += sz[pRoot]; //q的集合大小合并
}

2.3 查找当前顶点的父节点 find(element)

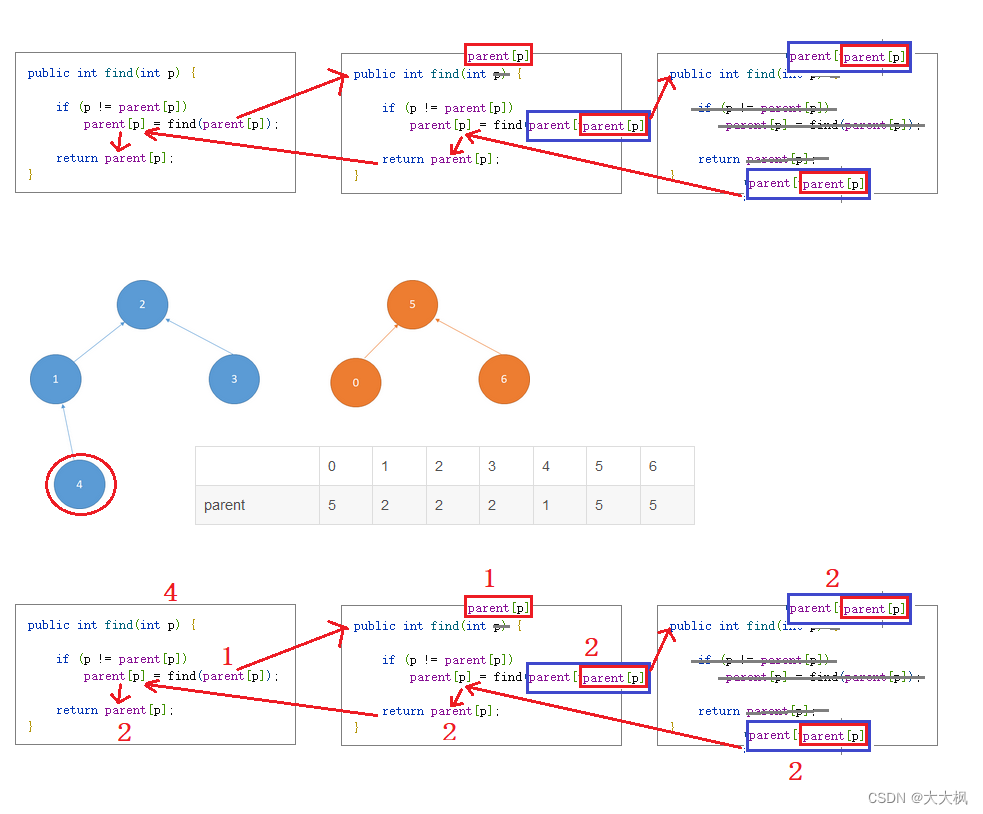
递归查找父节点，只要不满足p = parent[p]，就肯定没有到达最上层。find(parent[p])为查找p节点的

public int find(int p) {

    if (p != parent[p]) //还没找到根节点
        parent[p] = find(parent[p]); //递归实现
    
    //p = parent[p]时，就是父节点
    return parent[p]; 
}

在这里插入图片描述

3. 完整代码

public class Union_Find {
    class UF {
        private int[] parent; //parent数组中保存着每个节点所指向的父节点的索引
        private int[] sz;

        public UF(int n) {
            parent = new int[n];
            sz = new int[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i; //初始化的时候当前节点的父节点都是自己
                sz[i] = 1; //当前所属集合的大小
            }
        }
        
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        public int find(int p) {
            if (p != parent[p]) //还没找到根节点
                parent[p] = find(parent[p]); //递归实现
            return parent[p]; //终于找到根节点
        }

        public boolean isConnected(int p, int q) {
            return find(p) == find(q);
        }

        public void unionElements(int p, int q) {

            int pRoot = find(p); //找到p的父节点
            int qRoot = find(q); //找到q的父节点

            if (pRoot == qRoot)//如果pq的父节点相同，说明在同一个集合内
                return;

            parent[pRoot] = qRoot; //如果不相同，将p的父节点挂到q的父节点下，进行合并
            sz[qRoot] += sz[pRoot]; //q的集合大小合并
        }

        public int size(int p) {
            return sz[find(p)];
        }
    }

    private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    private int R, C;

    public int maxAreaOfIsland(int[][] grid) {

        if (grid == null) return 0;

        R = grid.length;
        if (R == 0) return 0;

        C = grid[0].length;
        if (C == 0) return 0;

        UF uf = new UF(R * C);
        for (int v = 0; v < R * C; v++) {
            int x = v / C, y = v % C;
            if (grid[x][y] == 1)
                for (int d = 0; d < 4; d++) {
                    int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
                    if (inArea(nextx, nexty) && grid[nextx][nexty] == 1) {
                        int next = nextx * C + nexty;
                        uf.unionElements(v, next);
                    }
                }
        }

        int res = 0;
        for (int v = 0; v < R * C; v++) {
            int x = v / C, y = v % C;
            if (grid[x][y] == 1)
                res = Math.max(res, uf.size(v)); //遍历找到最大的size
        }
        return res;
    }

    private boolean inArea(int x, int y) {
        return x >= 0 && x < R && y >= 0 && y < C;
    }
}