图论03-【无权无向】-图的深度优先DFS遍历-路径问题/检测环/二分图

1. 代码仓库

https://github.com/Chufeng-Jiang/Graph-Theory

2. 单源路径

2.1 思路

1. 构造visited数组和pre数组
   1.1 visited数组记录当前节点是否访问过
   也可以不使用visited数组，pre数组全部初始化为-1，联通的顶点对应的pre数组的值为前一个节点，pre数组中值为-1的都是不连通的顶点。
   1.2 pre数组记录当前节点的前一个节点
2. 使用pre数组对终点进行反推回源点，并记录
3. 将终点到原点的路径，反序输出

2.2 主要代码

   public SingleSourcePath(Graph G, int s){ //单源路径，要把源s传进来，而且只考虑与s连通的顶点，不连通的不考虑

        G.validateVertex(s);

        this.G = G;
        this.s = s;
        visited = new boolean[G.V()];
        pre = new int[G.V()];

        dfs(s, s);
    }

    private void dfs(int v, int parent){ //参数一：当前顶点； 参数二：上一个顶点

        visited[v] = true;
        pre[v] = parent;

        for(int w: G.adj(v)) //跟v相邻的所有顶点，相当于v是源，遍历与当前顶点相邻的所有点
            if(!visited[w])
                dfs(w, v); //（顶点，源）
    }
    
     public Iterable<Integer> path(int t){ //从源到t的路径

	     ArrayList<Integer> res = new ArrayList<Integer>();
	     if(!isConnectedTo(t)) return res;	
	     int cur = t; // 从t往回找
	     
	     while(cur != s){
	         res.add(cur); //添加当前节点（循环内不包含源）
	         cur = pre[cur]; //pre[cur]的值是cur的上一个节点
	     }
	     
	     res.add(s); //添加源
	     Collections.reverse(res);
	     return res;
 }

3. 所有点对路径

3.1 思路

对所有顶点进行遍历，创建每一个点的单源路径数组。

3.2 主要代码

public AllPairsPath(Graph G){
    this.G = G;
    paths = new SingleSourcePath[G.V()];
    for(int v = 0; v < G.V(); v ++)
        paths[v] = new SingleSourcePath(G, v);
}

4. 路径问题的优化-提前结束递归

4.1 思路

在填充visited和pre数组的时候，如果遇到了目标节点，直接结束。剩下的节点不进行处理。

if(v == t) return true; //程序出口，当到达t顶点时，返回true提前结束递归，而不仅仅是返回return

4.2 主要代码

    private boolean dfs(int v, int parent){

        visited[v] = true;
        pre[v] = parent;

        if(v == t) return true; //程序出口，当到达t顶点时，返回true提前结束递归，而不仅仅是返回return

        for(int w: G.adj(v)) //遍历与v相邻的顶点
            if(!visited[w]) //如果相邻的顶点没有被访问过
                if(dfs(w, v)) //递归遍历相邻的顶点，如果到达 v==t，则值为true
                    return true; //提前返回true

        return false; // 转一圈没法达到t，就可以返回false
    }

5. 检测环

5.1 思路

从某一点v出发，找到了点w，w被访问过，并且w不是v的前一个节点

5.2 主要代码

public CycleDetection(Graph G){
    this.G = G;
    visited = new boolean[G.V()];

    //要对所有的连通分量进行环检测
    for(int v = 0; v < G.V(); v ++)
        if(!visited[v])  //如果没有访问过
            if(dfs(v, v)){ //则进行深度搜索，如果深度搜索出来的是true，说明有环，则进入循环break
                hasCycle = true;
                break;
            }
}

    
private boolean dfs(int v, int parent){
    visited[v] = true;

    for(int w: G.adj(v))
        if(!visited[w]){ //case1：如果w没有被访问过
            if(dfs(w, v)) //如果dfs返回true，则说明有环。因为dfs有环才会返回true，那么进入if选择语句return true提前结束
                return true;
        }
        else if(w != parent) // case2：从v出发，找到了w，w还被访问过，并且w不是v的前一个节点
            return true; // 此时找到了环

    //其他的情况，找一圈没有找到环，返回false
    return false;
}

6. 二分图

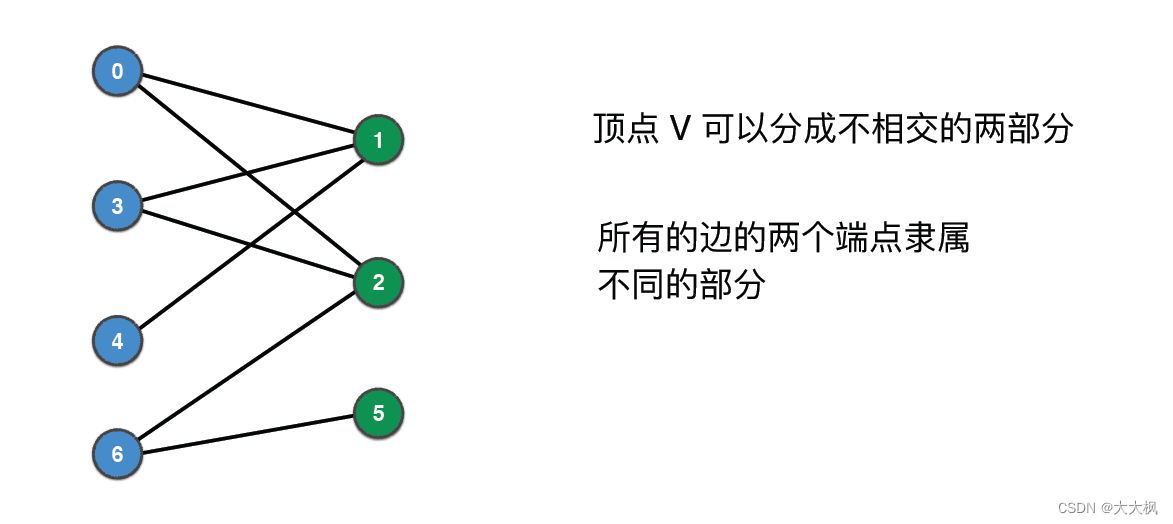
6.1 思路

二分图可以通过染色过程把顶点区分开，
[-1:顶点还没染色]
[0:一种颜色]
[1:另外一种颜色]

6.2 主要代码

6.2.1 遍历每个联通分量

1. dfs(v, 0) 返回true代表相连的两点颜色不一样，暂未出现矛盾；
2. dfs(v, 0) 返回false代表相连的两点颜色一样，不符合二分图的定义，因此进入if语句块，设置isBipartite = false;并且提前结束循环。

for(int v = 0; v < G.V(); v ++)
    if(!visited[v]) //如果没有被访问
    // 起始的时候把v统一染成0色，如果dfs返回的false，进入下面结构体，否则跳出执行v++
        if(!dfs(v, 0)){ 
            isBipartite = false; // 检测出错了，就设置成false
            break; // 后续的循环就不需要进行了
        }

6.2.2 递归判断相邻两点的颜色是否一致

private boolean dfs(int v, int color){  //参数一：顶点   参数二：颜色
    visited[v] = true;
    colors[v] = color;

    //依次判断相邻顶点w的颜色
    for(int w: G.adj(v))
        if(!visited[w]){ //如果w没有被访问过，则进入判断
            if(!dfs(w, 1 - color)) //如果v的颜色是0，那么w的颜色应该是1。如果v的颜色是1，那么w的颜色应该是0.
                return false; //如果相邻的两个顶点颜色一样，那么就不是二分图
        }
        else if(colors[w] == colors[v]) //如果相邻的两个顶点颜色一样，那么就不是二分图
            return false;

        return true;
}