2021年第43周总结
10.31
CF ECR 116
Problem D
首先集合大小比较应该保证,kkk左边的红色集合中的最小值大于蓝色集合中的最大值,kkk右边蓝色集合中的最小值应该大于蓝色集合中的最大值。
其次,枚举kkk,考虑每一行中以kkk为分界线的最小值和最大值,可以使用前后缀最大小值来解决。
首先,初始化将所有的列染成蓝色,然后将所有列按照列中最小值排序,从最大的开始染成红色,然后依次检查剩下的蓝色列,如果有不满足的一定要染成红色。根据左边的维护过程,连带维护右边的即可,可以使用multiset维护。
思路:过程模拟。
难点:最大最小值维护。
Problem E
计数DP好题。
设dp[x][j]dp[x][j]dp[x][j]为有xxx人,生命值的最大值为jjj的方案数,我们枚举在第一轮中死了kkk个人,那么这kkk个人的位置可能在(xk)\binom{x}{k}(kx),且生命值的可能性有min(x−1,j)\min(x - 1,j)min(x−1,j)个,因此这kkk个人的方案数为(xk)×min(x−1,j)k\binom{x}{k} \times \min(x - 1,j)^k(kx)×min(x−1,j)k,然后递归地考虑剩下的x−kx-kx−k个人,因为x−kx-kx−k人必须还活着,那么方案数等同于dp[x−k][max(j−(x−1),0)]dp[x-k][\max(j - (x-1),0)]dp[x−k][max(j−(x−1),0)](上限不能超过j−(x−1)j - (x-1)j−(x−1)),因此状态转移方程为:
dp[x][j]=∑k=0x(xk)×min(x−1,j)k×dp[x−k][max(j−(x−1),0)] dp[x][j] = \sum_{k = 0}^{x} \binom{x}{k} \times \min(x - 1,j)^k \times dp[x-k][\max(j - (x-1),0)] dp[x][j]=k=0∑x(kx)×min(x−1,j)k×dp[x−k][max(j−(x−1),0)]
初始状态为∀k∈[0,j],dp[0][k]=1\forall k \in[0,j], dp[0][k]=1∀k∈[0,j],dp[0][k]=1。
思路:计数DP。
难点:DP状态设计,转移方程,从死亡人数入手。
CF 752
Problem C
LCM半结论题,lcm(1…22)\text{lcm}(1\ldots22)lcm(1…22)就已经超过1e91e^91e9,因此内层循环不会超过202020次。
Problem D
数论好题。
当x>yx > yx>y的时候,很显然n=x+yn = x + yn=x+y 即可。难点在x≤yx \leq yx≤y。
考虑处理模式的第一种方案,化为定义式:
n−⌊nx⌋x=y−⌊yn⌋n n - \lfloor \frac{n}{x} \rfloor x = y - \lfloor \frac{y}{n} \rfloor n n−⌊xn⌋x=y−⌊ny⌋n
考虑整除式不好处理,因此这种办法大概不行。
考虑第二种方法,化为倍数式:
n=ax+ry=bn+ry=abx+(b+1)r n = ax+r \\ y = bn + r\\ y = abx + (b + 1)r n=ax+ry=bn+ry=abx+(b+1)r
存在三个未知变量也不太好处理,但是评论区有人用这种方法枚举aaa和bbb居然过了,神奇。
正解是第三种处理模式的方法,也是我不知道的,画图法。
考虑离yyy最近的那个kxkxkx,当nnn正好为他们两个的中点的时候,此时nnn对xxx取模(左箭头)正好等于yyy对nnn取模(右箭头)。又因为题目中xxx和yyy都为偶数,因此中点必然是一个整数。
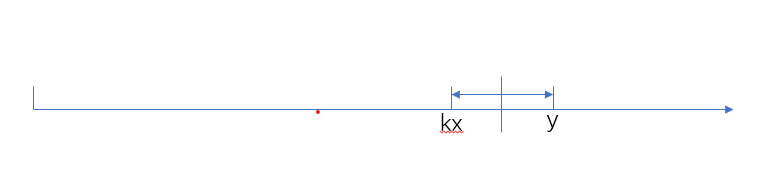
思路&难点:用画图法处理模式。
ABC 225
Problem F
DP好题,经过这题我对DP又有了深一层的理解。
先考虑拼接顺序问题,考虑如何固定拼接顺序,很显然根据排序规则Si+Sj<Sj+SiS_i + S_j < S_j + S_iSi+Sj<Sj+Si,排序即可,这样可以保证,任意选择kkk个字符串,按照排序完的相对顺序拼接,就是这kkk个字符串任意拼接的最优次序。
其次,考虑如何处理选择这jjj个字符串,有个很显然的DP方案,令dp[i][j]dp[i][j]dp[i][j]为前iii个字符串中选择jjj个字符串的最优答案,转移方程:
dp[i][j]=min(dp[i−1][j],dp[i−1][j−1]+Si) dp[i][j] = \min(dp[i - 1][j],dp[i - 1][j - 1] +S_i) dp[i][j]=min(dp[i−1][j],dp[i−1][j−1]+Si)
但是这么做是错的,必须从后向前更新DP才是正确的,即:
dp[i][j]=min(dp[i+1][j],Si+dp[i+1][j−1]) dp[i][j] = \min(dp[i + 1][j],S_i + dp[i + 1][j - 1]) dp[i][j]=min(dp[i+1][j],Si+dp[i+1][j−1])
原因如图:
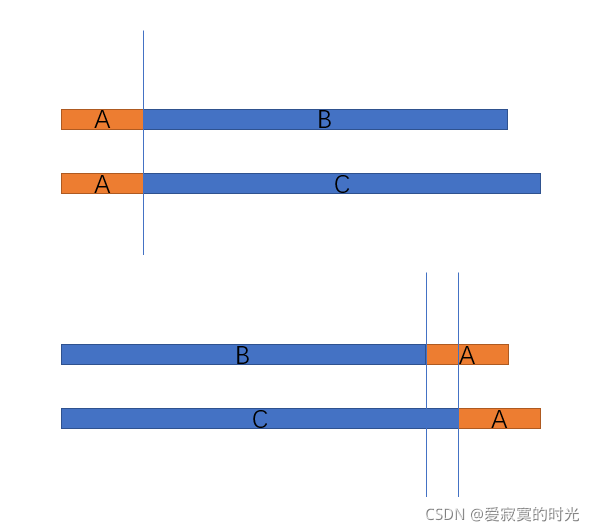
AAA即为SiS_iSi,BBB和CCC分别为递归答案。
最上面的一组是从后往前DP的过程,BBB和CCC字典序的顺序完全取决于BBB和CCC本身,并没有后效性,但是下面那组从前往后更新DP,BBB和CCC字典序的顺序并不完全取决于BBB和CCC本身,还取决于AAA,即AAA影响了前序DP的状态,具有后效性。
此题可以当做后向遍历解决DP后效性的模板题。
思路:排序+DP
难点:对DP后效性的理解





 博客内容涉及多项编程竞赛的题目解析,重点讨论了动态规划在解决问题中的应用。介绍了ProblemD的计数DP解法和ProblemE的优化策略,强调了状态设计与转移方程的重要性。同时,提及了其他问题的解决方案,如LCM计算和数论问题。文章通过实例深入浅出地阐述了如何运用画图法和排序来解决复杂问题。
博客内容涉及多项编程竞赛的题目解析,重点讨论了动态规划在解决问题中的应用。介绍了ProblemD的计数DP解法和ProblemE的优化策略,强调了状态设计与转移方程的重要性。同时,提及了其他问题的解决方案,如LCM计算和数论问题。文章通过实例深入浅出地阐述了如何运用画图法和排序来解决复杂问题。
















 284
284

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








