【2】深度神经网络的损失函数/激活函数

1.平方差损失函数 && Sigmoid激活函数

1.1 Sigmoid函数

       Sigmoid函数的表达式为：$$\sigma (z)=\frac{1}{1+e^{-z}}$$       对应的函数图像为：

       观察图像可发现，Sigmoid函数将输入的实数值压缩到(0,1)的实数范围内。更进一步地说，Sigmoid函数将很大的负数变为了0，将很大的正数变为了1。

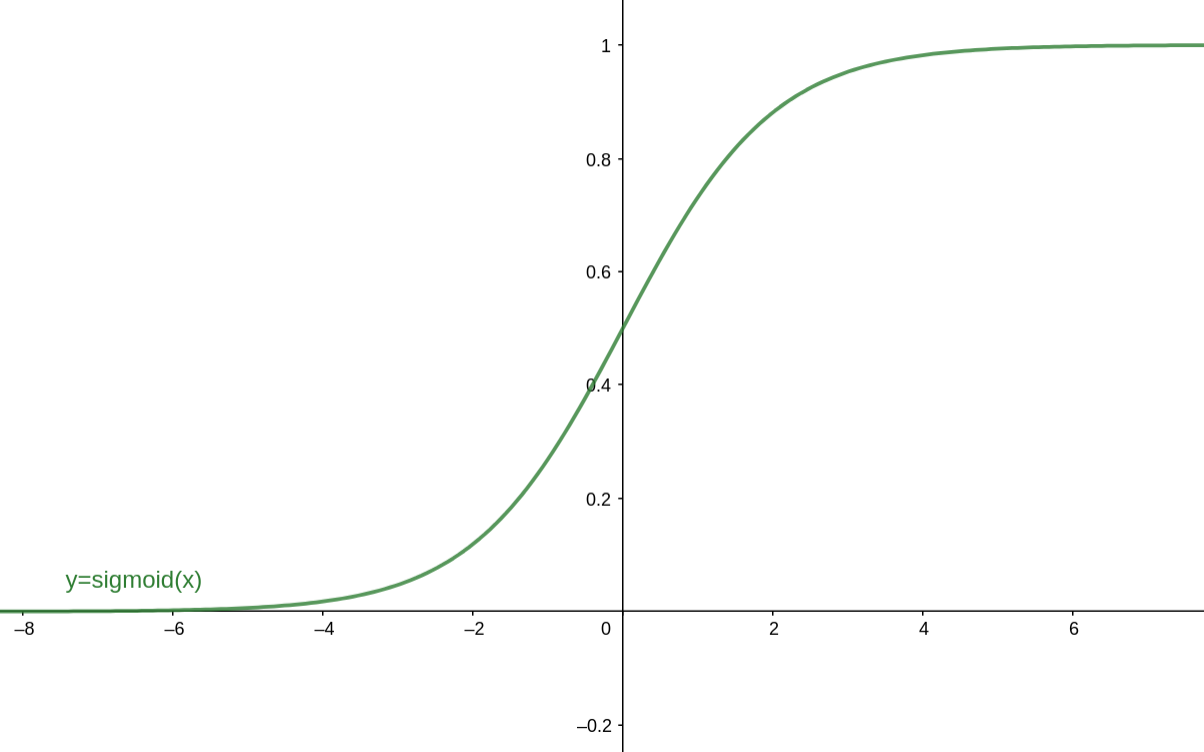
       在以前，Sigmoid函数因为具有良好的神经元激活频率的解释（从完全不激活0到完全激活状态1），经常被用作神经网络的激活函数，然而现在不太受欢迎了，主要是因为以下三个缺点：

1.Sigmoid函数饱和时使梯度消失。Sigmoid神经元有一个不好的特性，就是当神经元的激活值在接近0或1处会饱和，在这些区域，会导致梯度几乎为0（从图像可以看到，导数值几乎为0）！回顾一下，在反向传播的时候，我们更新$W^l和b^l$梯度时，都会乘上Sigmoid的梯度，如果这个Sigmoid的梯度非常小，那么就会导致相乘的最终结果为接近0，即导致梯度消失。（文章下面会有详细公式说明）

2.Sigmoid函数的输出不是零中心的，这没有满足我们想要的性质。在神经网络后面层中的神经元，得到的输入值（上一层的激活值）数据不是零中心的，如果输入的数据总是正数，那么关于w的梯度，在反向传播的过程中，将会要么全是正数，要么全是负数，导致梯度更新时，权重出现Z字型抖动，导致收敛的速度会变得很慢。不过如果采用批量梯度下降法时，整个批量的数据的梯度加起来，权重的更新会有不同的正负，收敛速度加快，因此相比于上个问题而言，这只是一个小问题。

3.Sigmoid函数中，涉及到指数运算，相比于其他的激活函数而言，这个计算起来较慢。

1.2 平方差损失函数在反向传播时的$W^l和b^l$梯度更新式

       根据上一节所学，可知梯度的计算如下：
$$\begin{array}{rl}\frac{\partial J(W,b,a,y)}{\partial W^l}& =\frac{\partial J(W,b,a,y)}{\partial z^l}\frac{\partial z^l}{\partial W^l}={\delta }^l{\left(a^{l-1}\right)}^T\\ & \\ \frac{\partial J(W,b,a,y)}{\partial b^l}& =\frac{\partial J(W,b,a,y)}{\partial z^l}\frac{\partial z^l}{\partial b^L}={\delta }^l\end{array}$$       其中，${\delta }^l$为：
$${\delta }^l={\delta }^{l+1}\frac{\partial z^{l+1}}{\partial z^l}={\left(W^{l+1}\right)}^T{\delta }^{l+1}\odot {\sigma }^{\prime }\left(z^l\right)$$       因为是反向传播，所以在计算${\delta }^l$时，$W^{l+1}$和${\delta }^{l+1}$都是已知的。

       然后再按照梯度下降，更新$W^l和b^l$值如下：
$$W^l=W^l-\alpha \frac{\partial J(W,b,a,y)}{\partial W^l}$$$$b^l=b^l-\alpha \frac{\partial J(W,b,a,y)}{\partial b^l}$$
       这里从公式的角度，印证了上面的观点，平方差损失函数&&Sigmoid激活函数的组合，在进行梯度更新时，梯度式子里包含了${\sigma }^{\prime }(z)$项，很容易因为激活函数的梯度趋近于0而导致整体梯度式子的值为0，即发生梯度消失！

2.交叉熵损失函数 && Sigmoid激活函数

2.1 交叉熵损失函数

       在之前的学习中，我们有了解到，交叉熵损失函数实际上是从KL散度推导出来的，用来比较两个变量分布的差异程度，交叉熵越小，表示两个分布差异越小，先来看看二分类任务中，交叉熵损失函数的定义：
$$H(y,\hat{y})=-[y\ln \hat{y}+(1-y)\ln (1-\hat{y})]$$       这里我们为了同上面平方差损失函数的表示一致，定义二分类任务中，每个样本的交叉熵损失函数为：
$$J(W,b,a,y)=-[y\ln a+(1-y)\ln (1-a)]$$       使用了交叉熵损失函数时，先来看看输出层${\delta }^L$的梯度情况：$$\begin{array}{rl}{\delta }^L& =\frac{\partial J\left(W,b,a^L,y\right)}{\partial z^L}\\ & \\ & =-y\frac{1}{a^L}\left(a^L\right)\left(1-a^L\right)+(1-y)\frac{1}{1-a^L}\left(a^L\right)\left(1-a^L\right)\\ & \\ & =-y\left(1-a^L\right)+(1-y)a^L\\ & \\ & =a^L-y\end{array}$$       上式中应用了Sigmoid函数求导的性质，即：$${\left(a^L\right)}^{\prime }=\left(a^L\right)\left(1-a^L\right)$$       言归正传，我们惊喜的发现，使用交叉熵损失函数之后，我们的梯度式${\delta }^L$中不再包含${\sigma }^{\prime }(z)$项了，梯度只和预测值$a^L$与真实值 $y$的差值有关，既满足了我们训练神经网络的要求，“在训练过程中，真实值与预测值的误差越大，那么梯度下降的幅度就越大”，又加快了收敛的速度（少了${\sigma }^{\prime }(z)$的干扰），因此，在用Sigmoid函数作为激活函数的时候，交叉熵损失函数比平方差损失函数的效果更加出色！

       不过在隐藏层中，依旧会存在大量的累乘操作，还是会存在很多个${\sigma }^{\prime }(z)$项，因此交叉熵损失函数没办法解决梯度消失问题，只是说相对而言，可以加快参数$W,b$ 的收敛速度。

3.梯度消失与梯度爆炸

       简单来说，梯度消失和梯度爆炸，实际上属于一种情况，在反向传播的过程中，由于我们使用了矩阵求导的链式法则，有一大串的连乘操作，如果连乘的数字都是小于1的，则梯度越往前乘就越小，最终趋近于0，梯度更新的信息量以指数形式衰减，即“梯度消失”；如果连乘的数字都是大于1的，则梯度越往前乘就越大，梯度更新的信息量以指数形式增大，即“梯度爆炸”。

3.1 梯度消失

       梯度消失往往在两种情况下常发生，一是比较深的神经网络，二是采用了不合适的损失函数与激活函数，如上面提到的平方差损失&&Sigmoid激活函数。
       如下图所示，一个简单的深度神经网络，一共有5层，每层只有一个神经元。

       定义损失函数用C表示，那么w1的梯度为：

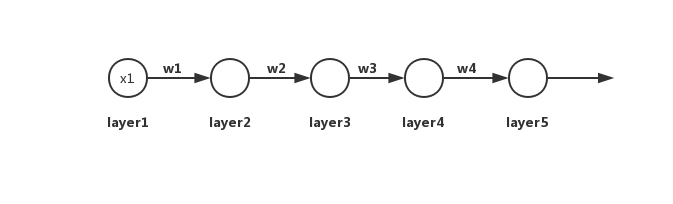
$$\frac{\partial C}{\partial w_1}=\frac{\partial C}{\partial a_5}\frac{\partial a_5}{\partial z_5}\frac{\partial z_5}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_1}$$

$$=\frac{\partial C}{\partial a_5}{\sigma }^{\prime }\left(z_5\right)w_4{\sigma }^{\prime }\left(z_4\right)w_3{\sigma }^{\prime }\left(z_3\right)w_2{\sigma }^{\prime }\left(z_2\right)x_1$$
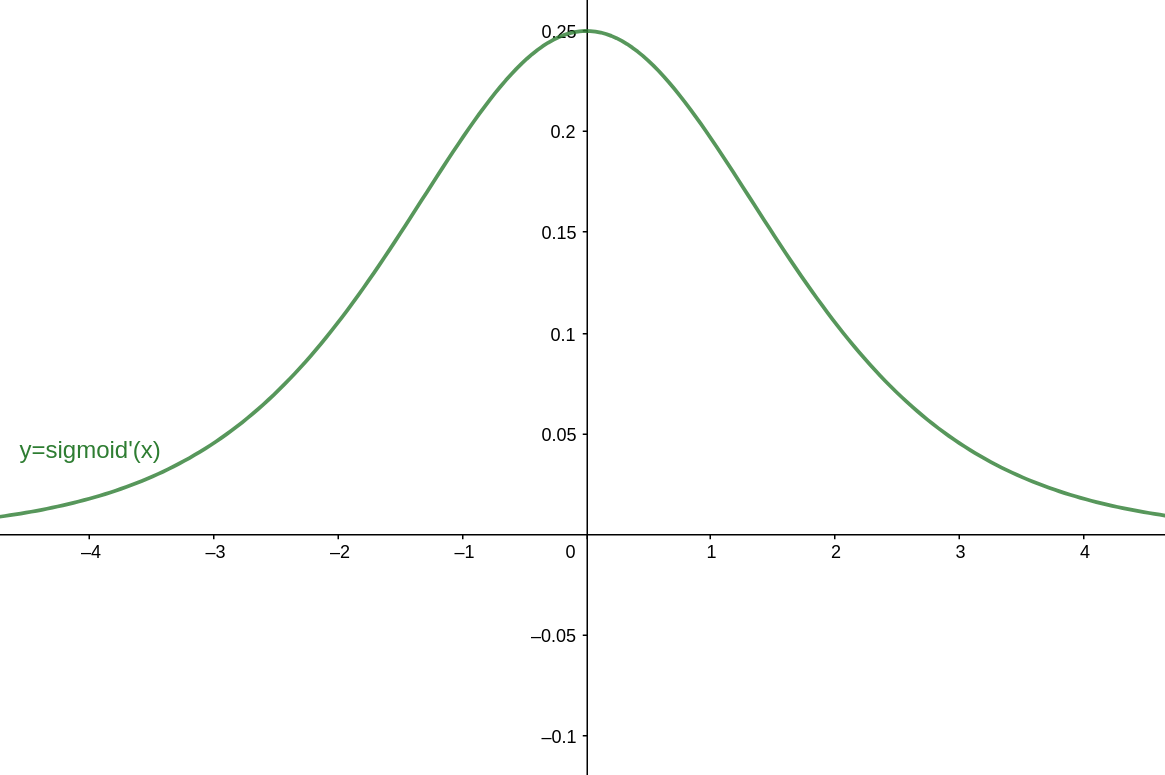
       而Sigmoid的导函数${\sigma }^{\prime }(z)$图像如下图所示：

        观察发现，导函数最大值为0.25,是一个小于1的值，如果我们初始化的w值很小的话，最终得到的梯度结果，就是一个接近于0的值，导致梯度消失。进而导致$W^l和b^l$的值不会发生明显的改变，也就更加谈不上收敛了，对于网络层数较深的神经网络，遇到梯度消失的问题，暂时没有比较好的解决办法，不过设置ReLU函数作为激活函数颇具成效，函数式为$\sigma (z)=\max (0,z)$，它对应的导函数为0或1。

3.2 梯度爆炸

       梯度爆炸的产生原因和上面类似，主要是因为连乘项中，初始化的权重值过大，导致每一层的$w_i{\sigma }^{\prime }(z_i)$的值大于1，最终连乘起来得到一个很大的梯度值。其实对比于梯度消失的话，在激活函数是Sigmoid函数时，梯度爆炸反倒不太容易发生。

       下面聊一聊如何解决梯度爆炸的情况。

1.设置梯度剪切阈值，如果超过了该阈值，直接将梯度置为该值;
2.降低梯度更新式中的学习率
3.权重正则化

3.3 拓展

       在深度神经网络中，梯度消失、梯度爆炸产生的根本原因在于反向传播训练法则，属于先天不足，Hinton提出capsule的原因就是为了彻底抛弃反向传播，如果真能大范围普及，那真的是一个革命。

4.常用的神经网络激活函数

4.1 tanh激活函数

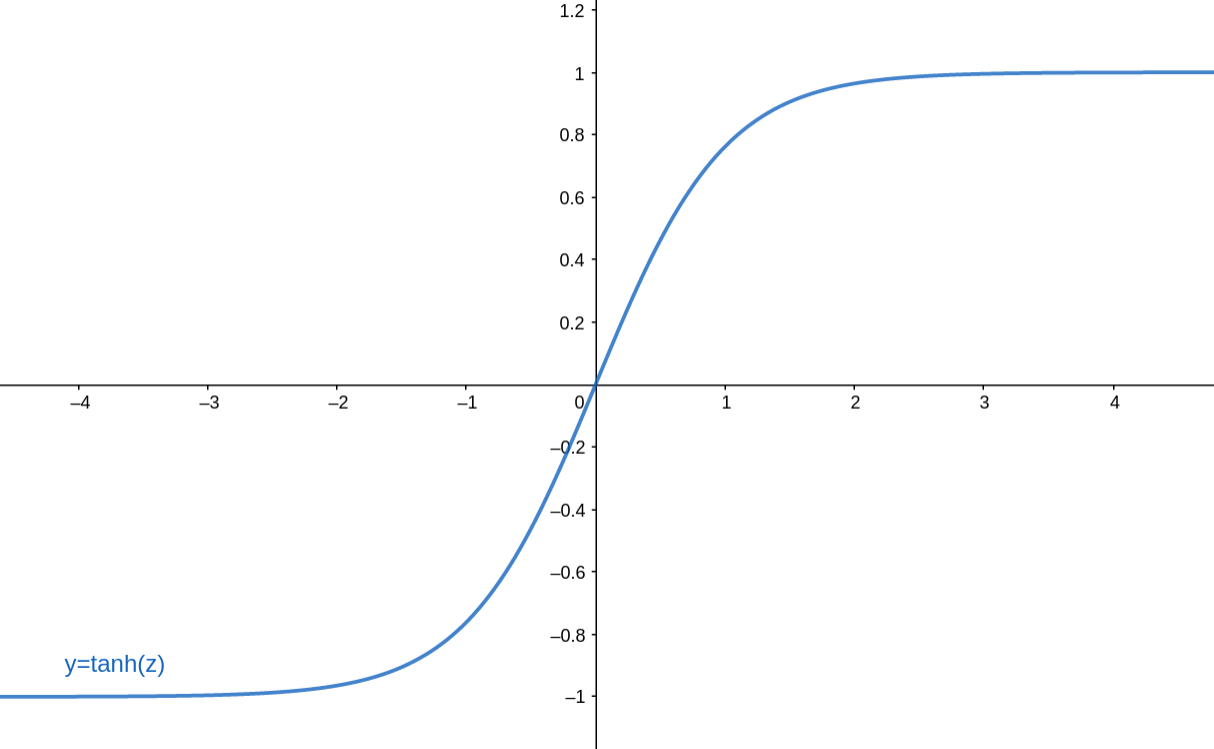
       tanh函数是Sigmoid函数的变种，表达式为：$$\tanh (z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$       tanh激活函数与Sigmoid激活函数的关系式为：（tanh函数实质上就是一个放大了并往下平移1位的Sigmoid函数）$$\tanh (z)=2\mathrm{sigmoid}(2z)-1$$       tanh函数图像如下：

       观察图像可发现，Sigmoid函数将输入的实数值压缩到(-1,1)的实数范围内。和Sigmoid函数一样，它也存在饱和问题（输入值往两边扩展时，对应的梯度值趋于0）,导致梯度消失。 不过它的优点在于输出是零中心的，因此在实际操作中，tanh激活函数与Sigmoid激活函数更受欢迎。

4.2 ReLU激活函数

       ReLU函数，全称是Rectified Linear Unit（修正线性单元），表达式为：$$f(x)=\max (0,x)$$       函数图像为：

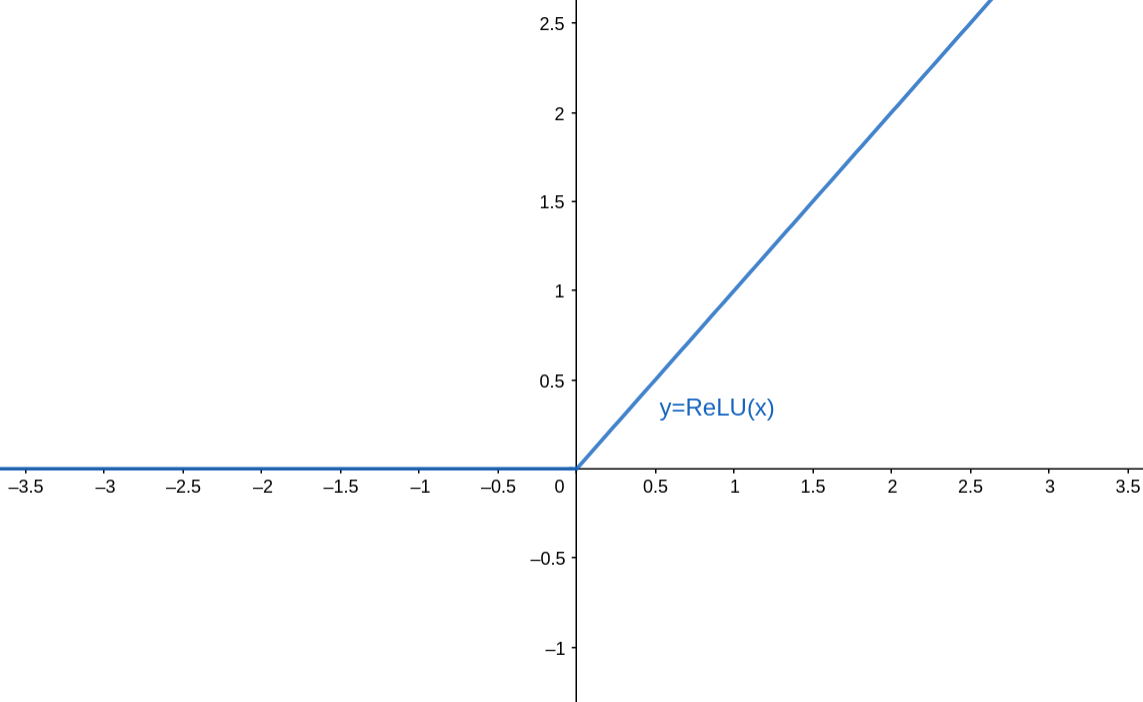
       对应的导函数图像为：

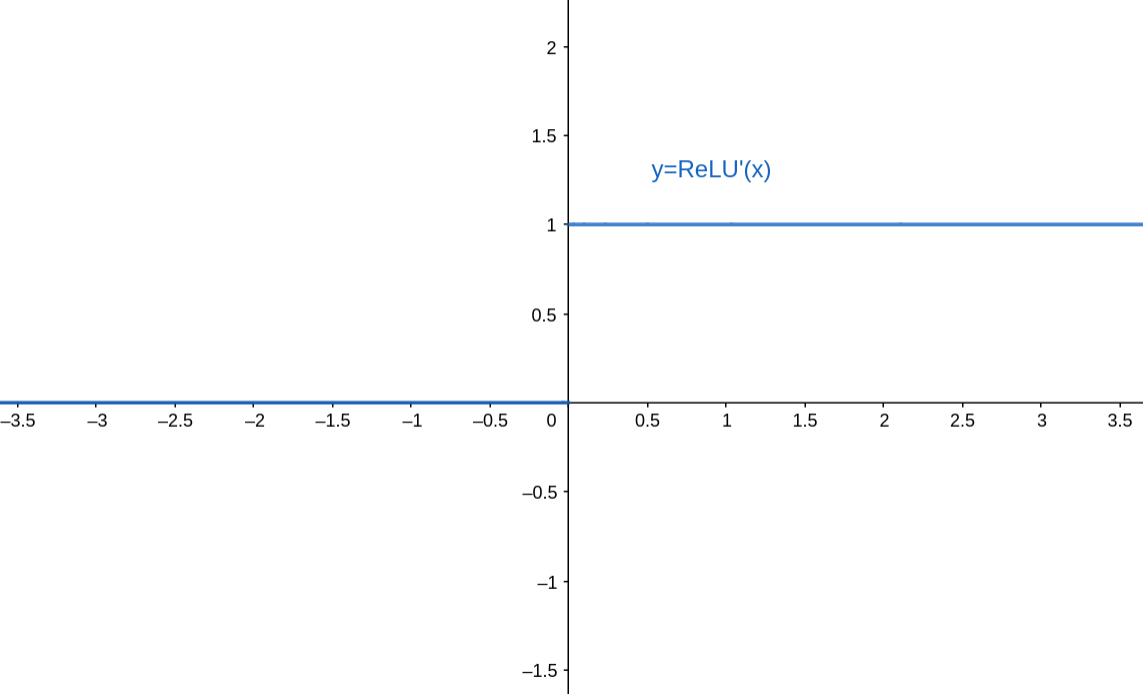
       我们可以很容易看出，ReLU函数的导数在正数部分是恒等于1的，因此在深层神经网络中使用ReLU激活函数就不会因为激活函数的梯度值，而导致出现梯度消失和爆炸的问题。

4.2.1 ReLU激活函数的优点：

       （1）相较于非线性的Sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用（ Krizhevsky 等的论文指出有6倍之多）。据称这是由它的非线性，非饱和的公式导致的；
       （2）Sigmoid和tanh神经元含有指数运算等耗费计算资源的操作，而ReLU可以简单地通过对一个矩阵进行阈值计算得到，不涉及到指数运算；

4.2.2 ReLU激活函数的缺点：

       在训练的时候，ReLU单元比较脆弱并且可能“死掉”。举例来说，当一个很大的梯度流过ReLU的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生，那么从此所有流过这个神经元的梯度将都变成0。也就是说，这个ReLU单元在训练中将不可逆转的死亡，因为这导致了数据多样化的丢失。例如，如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。通过合理设置学习率，这种情况的发生概率会降低。

       【疑问】如何理解ReLU神经元的“死亡”？

       对于任何输入，“死”的ReLU神经元总是输出相同的值(零)。（解释“死”的定义）
 
       出现这种情况，意味着ReLU神经元的输入始终为一个负数，即$z_j^l={\sum }_{i=1}^m{w}_{ji}^l{a}_i^{l-1}+b_j^l$的值始终为负数。为什么会这样子呢？下面举个例子说明：
 
       假设神经网络中传入了一个异常输入$x$,它的某一维特征$x_i$与$w_i$相乘之后，得到的值是一个很大的正数，于是经过ReLU函数激活之后，输出的值为也是一个很大的正数，最终神经网络的输出$a^L$与$y$的差异也很大，根据前面的学习我们知道，在反向传播时，将会产生一个很大的梯度值，根据bias项的梯度更新式，$b:=b-\eta \frac{\partial C}{\partial b}$，如果刚好学习率也设置的很大的话，那么b最终会变成一个值很小的负数，在之后进行常规输入时，$z_j^l$的值将会因为b，而大概率变为一个负数，对下一层输出0。
 
       一旦ReLU神经元最终处于这种死亡状态，它就不太可能恢复，因为0处的函数梯度也是0，所以梯度下降不会改变其权重W和bias项。针对此问题，改进后的Leaky ReLU可以解决此问题并提供给“死亡神经元”提供复活的可能性。
 
       Sigmoid和tanh神经元可能会遇到类似的问题，因为它们的值饱和了，但至少总有一个小的梯度（不至于为0）允许它们经过很长时间再恢复。

4.3 Leaky ReLU激活函数

      在上面有提到过，Leaky ReLU是为解决“ReLU死亡”问题的尝试。ReLU中当x<0时，函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值，比如0.01。所以其函数公式为$$f(x)=1(x<0)(\alpha x)+1(x>=0)(x)$$      其中$\alpha$是一个比较小的常量如0.01。有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU，把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在不同任务中均有益处的一致性并没有特别清晰。
      Leaky ReLU 函数图像如下：

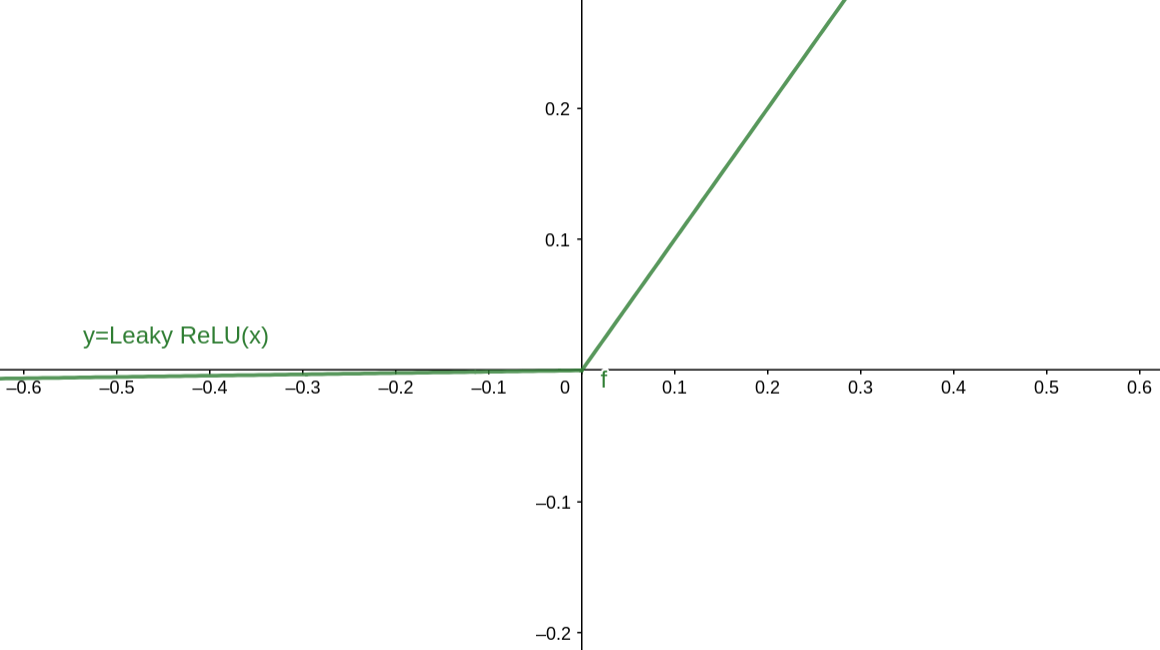
4.4 Maxout激活函数

      Maxout（由Goodfellow等发布）对于权重和输入值的内积结果不再使用函数形式，而是 $\max \left(W_1^{T}X+b_1,W_2^{T}X+b_2\right)$ 的形式，即有两组（或多组）不同的W矩阵和bias向量，Maxout是对ReLU和Leaky ReLU的一般化归纳，当$W_2，b_2=0$ 的时候，它就退化成ReLU神经元。这样Maxout神经元就拥有了ReLU的全部优点（非线性和不饱和），而没有它的缺点（死亡神经元），不过最大的缺点就是训练的参数变得更大，倍数增加。

4.5 小结

      到底用哪种神经元呢？推荐用ReLU激活函数，设置好学习率，或者监控神经网络中死亡神经元的占比，如果占比过高，可以尝试Leaky ReLU或者Maxout。实在不行，也可以试试$tanh$激活函数，尽量避免用Sigmoid激活函数（容易导致梯度消失，无法收敛）。

---

参考资料

1.刘建平Pinard《深度神经网络（DNN）损失函数和激活函数的选择》
2.CS231n课程讲义翻译：神经网络1
3.详解机器学习中的梯度消失、爆炸原因及其解决方法
4.谈谈由异常输入导致的 ReLU 神经元死亡的问题