【基础篇】PyTorch入门指南

本文是对 Neural Network Programming - Deep Learning with PyTorch 系列博客的翻译与整理，英语基础比较好的同学推荐阅读原汁原味的博客。

PyTorch是一个深度学习框架和一个科学计算包，这是PyTorch核心团队对PyTorch的描述，PyTorch的科学计算方面主要是PyTorch张量(tensor)库和相关张量运算的结果。A tensor is an n-dimensional array (ndarray)。PyTorch的torch.Tensor对象就是由Numpy的ndarray对象创建来的，两者之间的转换十分高效。PyTorch中内置了对GPU的支持，如果我们在系统上安装了GPU，那么使用PyTorch将张量在GPU之间来回移动是非常容易的一件事情。

1. PyTorch简介

  PyTorch的首次发布是在2016年10月，在PyTorch创建之前，还有一个叫做Torch(火炬)的框架。Torch是一个已经存在了很长时间的机器学习框架，它基于Lua编程语言。PyTorch和这个Lua版本(称为Torch)之间的联系是存在的，因为许多维护Lua版本的开发人员也参与了PyTorch的开发工作。你可能听说过PyTorch是由Facebook创建和维护的，这是因为PyTorch在创建时，Soumith Chintala(创始人)在Facebook AI Research工作。

  下表列出了PyTorch包及其相应的说明。这些是我们在本系列中构建神经网络时将学习和使用的主要PyTorch组件。

Package	Description
torch	顶层的PyTorch包和tensor库
torch.nn	一个子包，用于构建神经网络的模块和可扩展类
torch.autograd	一个子包，支持PyTorch中所有微分张量运算
torch.nn.functional	一种函数接口，包含构建神经网络的操作，如损失函数、激活函数和卷积操作。
torch.optim	一个子包，包含标准优化操作，如SGD和Adam
torch.utils	一个子包，包含数据集和数据加载器等实用工具类，使数据预处理更容易
torchvision	提供对流行数据集、模型体系结构和图像转换的访问的包

  为了优化神经网络，我们需要计算导数，为了进行计算，深度学习框架使用所谓的计算图(computational graphs)，计算图用于描述神经网络内部张量上发生的函数运算操作。

  PyTorch使用一个称为动态计算图的计算图，这意味着计算图是在创建操作时动态生成的，这与在实际操作发生之前就已完全确定的静态图形成对比。正因为如此，许多深度学习领域的前沿研究课题都需要动态图，或者从动态图中获益良多。

2. GPU相关介绍

  GPU是一种擅长处理特定计算(specialized computations)的处理器。这与中央处理器(CPU)形成对比，中央处理器是一种善于处理一般计算(general computations)的处理器。CPU是在我们的电子设备上支持大多数典型计算的处理器。

  GPU的计算速度可能比CPU快得多。 然而，这并非总是如此。 GPU相对于CPU的速度取决于所执行的计算类型。最适合GPU的计算类型是可以并行完成的计算。

  并行计算(paraller computing)是一种将特定计算分解成可以同时进行的独立的较小计算的计算方式，然后重新组合或同步计算结果，以形成原来较大计算的结果。

  一个较大的任务可以分解成的任务数量取决于特定硬件上包含的内核数量。核心是在给定处理器中实际执行计算的单元，CPU通常有4个、8个或16个核心，而GPU可能有数千个。

  有了这些工作知识，我们可以得出结论，并行计算是使用GPU完成的，我们还可以得出结论，最适合使用GPU解决的任务是可以并行完成的任务。如果计算可以并行完成，我们可以使用并行编程方法和GPU加速计算。

  现在我们把目光转移到神经网络上，看看为什么GPU在深度学习中被大量使用。 我们刚刚看到GPU非常适合并行计算，而关于GPU的事实就是深度学习使用GPU的原因。

   Neural networks are embarrassingly parallel.指的是一个任务分解为几个子任务之后，在不同处理器上执行该子任务，而这些子任务之间不会相互依赖，也就说明该任务十分适合于并行计算，也被称为embarrassingly parallel.

  我们用神经网络所做的许多计算可以很容易地分解成更小的计算，这样一组更小的计算就不会相互依赖了。卷积操作就是这样一个例子。

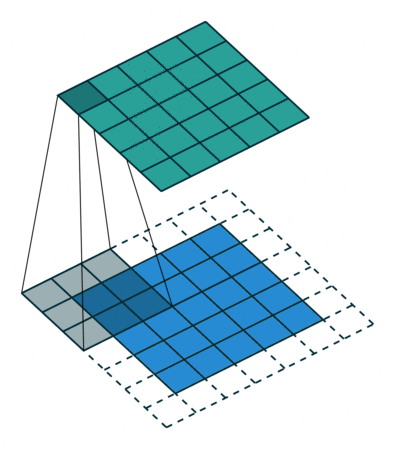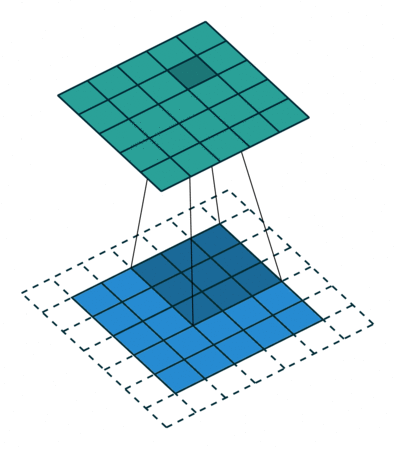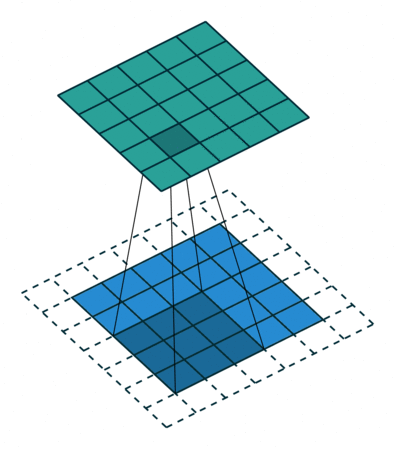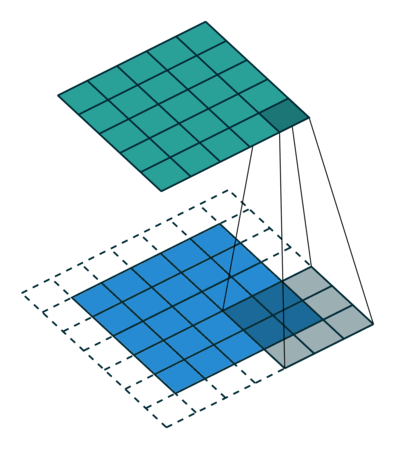
• 蓝色区域（底部）: Input channel
• 阴影区域（底部）: Filter
• 绿色区域（顶部）: Output channel

  对于蓝色输入通道上的每个位置，3 x 3过滤器都会进行计算，将蓝色输入通道的阴影部分映射到绿色输出通道的相应阴影部分。在动画中，这些计算一个接一个地依次进行。但是，每个计算都是独立于其他计算的，这意味着任何计算都不依赖于任何其他计算的结果。因此，所有这些独立的计算都可以在GPU上并行进行，从而产生整个输出通道，加速我们的卷积过程。

3. CUDA相关介绍

  Nvidia是一家设计GPU的技术公司，他们创建了CUDA作为一个软件平台，与GPU硬件适配，使开发人员更容易使用Nvidia GPU的并行处理能力来构建加速计算的软件。Nvidia GPU是支持并行计算的硬件，而CUDA是为开发人员提供API的软件层。

  开发人员通过下载CUDA工具包来使用CUDA，伴随工具包一起的是专门的库，如 cuDNN, CUDA Deep Neural Network library.

  在PyTorch中利用CUDA非常简单。如果我们希望在GPU上执行特定的计算，我们可以通过在数据结构(tensors)上调用cuda()来指示PyTorch这样做。

  假设我们有以下代码：

> t = torch.tensor([1,2,3])
> t
tensor([1, 2, 3])

  默认情况下，以这种方式创建的tensor对象在CPU上。因此，我们使用这个张量对象所做的任何操作都将在CPU上执行。

  现在，要把张量移到GPU上，我们只需要写：

> t = t.cuda()
> t
tensor([1, 2, 3], device='cuda:0')

  由于可以在CPU或GPU上有选择地进行计算，因此PyTorch的用途非常广泛。

  GPU是不是总是比CPU更好呢？答案是否定的。

  GPU只对特定的（专门的）任务更快。它也会遇到某些瓶颈，例如，将数据从CPU移动到GPU的成本很高（耗时），因此在这种情况下，如果计算任务本身就很简单，还把它转移到GPU上进行计算，那么总体性能可能会降低。

  把一些相对较小的计算任务转移到GPU上不会使我们的速度大大加快，而且可能确实会减慢我们的速度。GPU对于可以分解为许多较小任务的任务非常有效，如果计算任务已经很小，那么将任务移到GPU上就不会有太多收获。

4. 张量定义

  神经网络中的输入、输出和变换都是用tensor表示的，在神经网络编程中大量使用了tensor。

  张量的概念是其他更具体概念的数学概括，让我们看看张量的一些具体实例：

• number
• scalar
• array
• vector
• 2d-array
• matrix

  我们来把上面的张量实例分成两组：

• number, array, 2d-array
• scalar, vector, matrix

  第一组中的三个术语（数字、数组、二维数组）是计算机科学中常用的术语，而第二组（标量、矢量、矩阵）是数学中常用的术语。

  我们经常看到这种情况，不同的研究领域对同一概念使用不同的词。在深度学习中，我们通常把这些都称为tensor。

Indexes requried	Computer science	Mathematics
0	number	scala
1	array	vector
2	2d-array	matrix
n	nd-array	nd-tensor

5. 张量的秩、轴和形状

  在深度学习中，秩、轴和形状是我们最关心的tensor属性，这些概念建立在一个又一个的基础上，从秩开始，然后是轴，再到形状，请注意这三者之间的关系。

  我们在这里引入rank这个词，是因为它在深度学习中经常被用到，它指的是给定张量中的维数，一个张量的秩告诉我们需要多少索引来引用张量中的某一个特定元素。

  如果我们有一个张量，想要表示某一个特定的维度，那么在深度学习中使用轴(Axis)这个词。

  每个轴的长度告诉我们每个轴上有多少索引可用，假设我们有一个张量 t，我们知道第一个轴的长度为3，而第二个轴的长度为4。

  我们可以索引第一个轴的每一个元素像这样：

t[0]
t[1]
t[2]

  由于第二轴的长度为4，所以我们可以沿着第二轴标出4个位置。这对于第一轴的每个索引都是成立的，所以我们有：

t[0][0]
t[1][0]
t[2][0]

t[0][1]
t[1][1]
t[2][1]

t[0][2]
t[1][2]
t[2][2]

t[0][3]
t[1][3]
t[2][3]

  张量的形状是由每个轴的长度决定的，所以如果我们知道给定张量的形状，那么我们知道每个轴的长度，这告诉我们每个轴有多少个索引可用。

  我们结合一个实例来看看形状(shape)是如何计算的。

> a = torch.tensor([[[[1]],[[2]],[[3]]]])
> print(a)
tensor([[[[1]],

         [[2]],

         [[3]]]])

  如何来计算它的形状呢，首先我们数一下中括号的个数，得知这是一个四维张量，然后由外而内，去掉最外层的中括号之后，得到 tensor([[[1]], [[2]], [[3]]])，此时只有一个最外层的中括号，那我们的shape变为 $(1,,,)$；同理，我们继续去除最外层的中括号，得到 tensor([[1]], [[2]], [[3]])，此时有三个最外层的中括号，那我们的shape则变为 $(1,3,,)$，因为每一个维度的形状是相同的，于是我们继续来只需要看其中一个维度即可，即 tensor([[1]])；去除最外层的中括号，得到 tensor([1])，此时只有一个最外层的中括号，shape变为 $(1,3,1,)$；最后再去除一个中括号，得到 tensor(1)，shape变为 $(1,3,1,1)$，以上就是得到张量形状的全部过程。

> print(a.shape)
torch.Size([1, 3, 1, 1])

6. CNN中的张量

  CNN输入的形状，通常有4个维度，也就是说我们有一个秩为4的四阶张量，张量中的每一个索引对应着一个轴，每一个轴都代表着输入数据的某种实际特征，我们从右到左，来理解CNN输入的张量中，每个维度的含义。

  原始图像数据以像素的形式出现，用数字表示，并使用高度和宽度两个维度进行布局，所以我们需要 width 和 height 两个轴。

  下一个轴表示图像的颜色通道数，灰度图的通道数为1，RGB图的通道数为3，这种颜色通道的解释仅适用于输入张量，后续 feature map 中的通道都不是代表颜色。

  也就是说，张量中的最后三个轴，表示着一个完整的图像数据。在神经网络中，我们通常处理成批的样本，而不是单个样本，所以最左边的轴的长度，告诉我们一批中有多少个样本。

  假设给定张量的形状为 [3，1，28，28] ，那么我们可以确定，一个批次中有三幅图像，每张图像的颜色通道数为3，宽和高都是28。 [Batch, Channels, Height, Width]

  我们接下来看看张量被卷积层变换后，颜色通道轴的解释是如何变化的。

  假设我们有一个 tensor 的形状为 [1，1，28，28]，当它经过一个卷积层之后，张量的宽和高，以及通道数量都会发生改变，输出的通道数即对应着卷积层中卷积核的个数。

  输出的通道不再解释为颜色通道，而是 feature map 的修改通道（modified channels），使用 feature 一词是因为卷积层的输出，代表图像中的特定特征，例如边缘，这些映射随着网络在训练过程中的学习而出现，并且随着我们深入网络而变得更加复杂。

7. torch.Tensor类

  我们可以用下面的方式，构建一个 torch.Tensor 类的实例：

> t = torch.Tensor()
> type(t)
torch.Tensor

  每一个 torch.Tensor 对象都有3个属性：

> print(t.dtype)
> print(t.device)
> print(t.layout)
torch.float32
cpu
torch.strided

  我们来详细看一下dtype有哪些属性：

Data type	dtype	CPU tensor	GPU tensor
32-bit floating point	torch.float32	torch.FloatTensor	torch.cuda.FloatTensor
64-bit floating point	torch.float64	torch.DoubleTensor	torch.cuda.DoubleTensor
16-bit floating point	torch.float16	torch.HalfTensor	torch.cuda.HalfTensor
8-bit integer (unsigned)	torch.uint8	torch.ByteTensor	torch.cuda.ByteTensor
8-bit integer (signed)	torch.int8	torch.CharTensor	torch.cuda.CharTensor
16-bit integer (signed)	torch.int16	torch.ShortTensor	torch.cuda.ShortTensor
32-bit integer (signed)	torch.int32	torch.IntTensor	torch.cuda.IntTensor
64-bit integer (signed)	torch.int64	torch.LongTensor	torch.cuda.LongTensor

  注意，每种类型有一个CPU和GPU版本。关于张量数据类型，需要记住的一点是，张量之间的张量运算必须发生在具有相同类型数据的张量之间。

  device用来表示张量的数据是存储在 CPU 上还是 GPU 上。它决定来张量计算的位置在哪里。我们可以用 索引 的方式来指定设备的编号：

> device = torch.device('cuda:0')
> device
device(type='cuda', index=0)

  使用多个设备时，需要记住的一点是张量之间的张量运算必须发生在同一设备上的张量之间。

  layout属性用来指定张量在内存中是如何存储的。

  在 PyTorch 中，可以通过以下四种方式将一个 array-like 的对象转成 torch.Torch 的对象。

torch.Tensor(data)
torch.tensor(data)
torch.as_tensor(data)
torch.from_numpy(data)

  我们可以直接创建一个 Python list 类型的 data，不过 numpy.ndarray 是一个更加常见的选择，如下所示：

> data = np.array([1,2,3])
> type(data)
numpy.ndarray

  然后再用上面的四种方式来创建一个 torch.Torch 的对象：

> o1 = torch.Tensor(data)
> o2 = torch.tensor(data)
> o3 = torch.as_tensor(data)
> o4 = torch.from_numpy(data)

> print(o1)
> print(o2)
> print(o3)
> print(o4)
tensor([1., 2., 3.])
tensor([1, 2, 3], dtype=torch.int32)
tensor([1, 2, 3], dtype=torch.int32)
tensor([1, 2, 3], dtype=torch.int32)

  除了第一个之外，其他的输出(o2、o3、o4)似乎都产生了相同的张量，第一个输出(o1)在数字后面有圆点，表示数字是浮点数，而后面三个选项的类型是int32。

> type(2.)
float
> type(2)
int

  当然，PyTorch 也内置了一些不需要通过数据转换，直接构成张量的方式。

> print(torch.eye(2))
tensor([
    [1., 0.],
    [0., 1.]
])

> print(torch.zeros([2,2]))
tensor([
    [0., 0.],
    [0., 0.]
])

> print(torch.ones([2,2]))
tensor([
    [1., 1.],
    [1., 1.]
])

> print(torch.rand([2,2]))
tensor([
    [0.0465, 0.4557],
    [0.6596, 0.0941]
])

8. 创建Tensor的方法对比

  先来看看 torch.tensor() 和 torch.Tensor() 这两种方法的区别：

> data = np.array([1,2,3])
> type(data)
numpy.ndarray

> o1 = torch.Tensor(data)
> o2 = torch.tensor(data)

> print(o1)
> print(o2)

tensor([1., 2., 3.])
tensor([1, 2, 3], dtype=torch.int32)

  torch.Tensor() 是 torch.Tensor 类的构造函数，torch.tensor()是工厂函数，它构造 torch.Tensor 对象并将它们返回给调用方，这是一种创建对象的软件设计模式，另一个区别就是前者默认的数据类型是浮点型，而后者是整型。数据类型可以显示地指定，不指定的话，可以通过传入的数据类型来推断。四种构造方法中只有 torch.Tensor() 函数不可以显示指定dtype。

> torch.tensor(data, dtype=torch.float32)
> torch.as_tensor(data, dtype=torch.float32)

  我们再来看看几种方法创建 tensor 时，对传入的 data 采取的是拷贝还是共享的方式。

> print('old:', data)
old: [1 2 3]

> data[0] = 0

> print('new:', data)
new: [0 2 3]

> print(o1)
> print(o2)
> print(o3)
> print(o4)

tensor([1., 2., 3.])
tensor([1, 2, 3], dtype=torch.int32)
tensor([0, 2, 3], dtype=torch.int32)
tensor([0, 2, 3], dtype=torch.int32)

  可以发现，torch.Tensor() 和 torch.tensor() 这两个函数都是对输入数据进行了拷贝，而 torch.as_tensor() 和 torch.from_numpy() 这两个函数则是对输入数据进行了共享的方式。与复制数据相比，共享数据效率更高，占用的内存更少，因为数据不会写入内存中的两个位置。

  如果我们想把 torch.Tensor 对象转成 ndarray 类型的话，采取下面这种方式：

> print(type(o3.numpy()))
> print(type(o4.numpy()))
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>

  不过这个方法只适用于 torch.as_tensor() 和 torch.from_numpy() 这两种方式创建的 torch.Tensor 对象，我们再来进一步比较一下这两个方法的区别。

  torch.from_numpy() 函数只接受 numpy.ndarray 类型的输入，而torch.as_tensor() 函数可以接受各种类似Python数组的对象，包括其他PyTorch张量。

  综上所述，我们更推荐 torch.tensor() 和 torch.as_tensor() 这两个函数，前者是一种直接调用的方式，后者是在需要调参的时候采用的方式。

  关于内存共享的机制，还有一些需要提的点：

• 由于numpy.ndarray对象是在CPU上分配的，因此当使用GPU时，torch.as_tensor() 函数必须将数据从CPU复制到GPU。
• torch.as_tensor() 的内存共享不适用于内置的Python数据结构，如列表。
• torch.as_tensor() 的调用要求开发人员了解共享特性。这是必要的，这样我们就不会在没有意识到变更会影响多个对象的情况下无意中对底层数据进行不必要的更改。
• 当 numpy.ndarray 对象和张量对象之间有许多来回操作时，torch.as_tensor() 性能的优越性会更大。

9. tensor的reshape、squeeze和cat操作

  假设我们现在有一个秩为 2 、形状为 3 * 4 的张量：

> t = torch.tensor([
    [1,1,1,1],
    [2,2,2,2],
    [3,3,3,3]
], dtype=torch.float32)

  在 PyTorch 中，我们有两种获取张量形状的方法：

> t.size()
torch.Size([3, 4])

> t.shape
torch.Size([3, 4])

  我们还可以采用下面的方式来获取张量的元素数：

> torch.tensor(t.shape).prod()
tensor(12)

> t.numel()
12

  于是我们可以进行 reshape 操作：

> t.reshape([1,12])
tensor([[1., 1., 1., 1., 2., 2., 2., 2., 3., 3., 3., 3.]])

> t.reshape([2,6])
tensor([[1., 1., 1., 1., 2., 2.],
        [2., 2., 3., 3., 3., 3.]])

> t.reshape([3,4])
tensor([[1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])
        
> t.reshape(6,2)
tensor([[1., 1.],
        [1., 1.],
        [2., 2.],
        [2., 2.],
        [3., 3.],
        [3., 3.]])
        
> t.reshape(12,1)
tensor([[1.],
        [1.],
        [1.],
        [1.],
        [2.],
        [2.],
        [2.],
        [2.],
        [3.],
        [3.],
        [3.],
        [3.]])

  我们传入的参数有 ([2, 6]) 和 (2, 6) 两种方式，这个都是可行的，但是我们要保证 传入参数的乘积和原始张量的元素个数要相等。

> t.reshape(2,2,3)
tensor(
[
    [
        [1., 1., 1.],
        [1., 2., 2.]
    ],

    [
        [2., 2., 3.],
        [3., 3., 3.]
    ]
])

   在 PyTorch 中，还有一个 view() 函数，功能和 reshape() 函数是一样的，都可以改变张量的形状。

> t.view(3,4)
tensor([[1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])
        
> t.view([2,6])
tensor([[1., 1., 1., 1., 2., 2.],
        [2., 2., 3., 3., 3., 3.]])

  我们还可以通过 squeeze() 和 unsqueeze() 这两个函数来改变输入张量的形状。

• 压缩(squeeze)一个张量可以去掉长度为1的维度。

• 解压缩(unsqueeze)一个张量可以增加一个长度为1的维度。

  从实际的例子来理解：

> a = torch.tensor([[[1]],[[2]]])
> print(a)
tensor([[[1]],

        [[2]]])
        
> print(a.squeeze())
tensor([1, 2])

> print(a.squeeze().unsqueeze(dim=0))
tensor([[1, 2]])

> print(a.squeeze().unsqueeze(dim=1))
tensor([[1],
        [2]])

  squeeze()函数还有一个广泛的用途就是作为flatten()函数的一个子函数：

def flatten(t):
    t = t.reshape(1, -1)
    t = t.squeeze()
    return t

> a = torch.tensor([[[[1]],[[2]],[[3]]]])
> print(a)
tensor([[[[1]],

         [[2]],

         [[3]]]])
         
> print(a.shape)
torch.Size([1, 3, 1, 1])

> print(a.reshape(1, -1)) 
tensor([[1, 2, 3]])  # torch.Size([1, 3])

> print(a.reshape(1, -1).squeeze()) # 可以看到实现了 flatten 的函数功能
tensor([1, 2, 3])

> print(a.reshape(1, -1).squeeze().shape)
torch.Size([3])

  PyTorch 还提供了一个 cat() 函数，来实现张量的拼接(concatenate)。假设我们有如下两个张量：

> t1 = torch.tensor([
    [1,2],
    [3,4]
])
> t2 = torch.tensor([
    [5,6],
    [7,8]
])

  我们可以将它们按行(axis=0)拼接：

> torch.cat((t1, t2), dim=0)
tensor([[1, 2],
        [3, 4],
        [5, 6],
        [7, 8]])

  也可以将它们按列(axis=1)拼接：

torch.cat((t1, t2), dim=1)
tensor([[1, 2, 5, 6],
        [3, 4, 7, 8]])

  拼接之后的shape，可以通过所选拼接维度的值进行求和得到：

> torch.cat((t1, t2), dim=0).shape
torch.Size([4, 2])

> torch.cat((t1, t2), dim=1).shape
torch.Size([2, 4])

10. flatten操作

  我们知道，CNN中的全连接层接收的是一个一维向量输入，而前面卷积层的输出都是 feature map 的形式，于是在全连接层之前，一定存在一个 flatten 操作，我们来看看，如何 flatten 张量中的某一个轴。

  首先创建三个张量，代表一个Batch中的三张图像：

> a = torch.ones(4,4)
> print(a)
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])


> b = torch.full((4,4),2)  # 此处的full()和numpy中的full()的作用类似
> print(b)
tensor([[2., 2., 2., 2.],
        [2., 2., 2., 2.],
        [2., 2., 2., 2.],
        [2., 2., 2., 2.]])

> c = torch.full((4,4),3)
> print(c)
tensor([[3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.]])

  CNN 中的 Batch 也是由单个张量表示的，于是我们需要将这三张图像连接起来，这里要用到 stack() 函数，后面会细讲。

> t = torch.stack((a,b,c))
> t
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.]],

        [[3., 3., 3., 3.],
         [3., 3., 3., 3.],
         [3., 3., 3., 3.],
         [3., 3., 3., 3.]]])
> t.shape
torch.Size([3, 4, 4])

  我们这里默认的图像是灰度图，即通道数为1，于是我们可以通过 reshape 或 unsqueeze 这两种方式，进一步修改我们的 tensor.

> t.reshape(3,1,4,4)
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]],
          
        [[[2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.]]],

        [[[3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.]]]])

> t.unsqueeze(dim=1)
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]],

        [[[2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.]]],

        [[[3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.]]]])

  现在我们得到了一个四维张量，我们需要 flatten 里面的每一个图像张量，而不是整个张量，不妨先看看有哪些 flatten 整个张量的方法。

> t.reshape(1,-1)[0]
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 2., 2.,
        2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3., 3., 3., 3.,
        3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.])
> t.reshape(-1)
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 2., 2.,
        2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3., 3., 3., 3.,
        3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.])
> t.view(t.numel())
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 2., 2.,
        2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3., 3., 3., 3.,
        3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.])
> t.flatten()
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 2., 2.,
        2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3., 3., 3., 3.,
        3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.])

  在 CNN 中我们需要对同一个Batch中的每一张图片进行预测，因此上面对整个 tensor 进行 flatten 的做法是不可取的，我们需要对 tensor 中的(channels, width, height) 这三个维度进行展开，而 flatten() 函数中提供了对指定维度展开的方法。

>> print(t)
tensor([[[[1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.],
          [1., 1., 1., 1.]]],

        [[[2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.],
          [2., 2., 2., 2.]]],

        [[[3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.],
          [3., 3., 3., 3.]]]])
          
> t.flatten(start_dim=1)
tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.],
        [3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.]])

> t.flatten(start_dim=2)
tensor([[[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]],

        [[2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2.]],

        [[3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3.]]])

  注意，这里的 start_dim 参数，用来指定从哪一个轴开始进行 flatten 操作，默认是0。我们原本张量 t 的shape为$(3,1,4,4)$，如果 start_dim=1，那么我们最后得到的shape为$(3,16)$；如果start_dim=2，那么我们最后得到的shape为$(3,1,16)$。

11. element-wise操作

  顾名思义，element-wise 类型操作表示两个张量中对应元素之间的操作，这要求两个张量的形状一致，假设我们有如下两个张量：

> t1 = torch.tensor([
    [1,2],
    [3,4]], dtype=torch.float32)

> t2 = torch.tensor([
    [9,8],
    [7,6]], dtype=torch.float32)

   加减乘除 都属于 element-wise 类型的操作：

> t1 + t2
tensor([[10., 10.],
        [10., 10.]])
        
> t1 - t2
tensor([[-8., -6.],
        [-4., -2.]])

> t1 * t2
tensor([[ 9., 16.],
        [21., 24.]])
        
> t1 / t2
tensor([[0.1111, 0.2500],
        [0.4286, 0.6667]])

   除此之外，张量与某个数值之间的加减乘除也是属于 element-wise 类型的操作：

> print(t + 2)
tensor([[3., 4.],
        [5., 6.]])

> print(t - 2)
tensor([[-1.,  0.],
        [ 1.,  2.]])

> print(t * 2)
tensor([[2., 4.],
        [6., 8.]])

> print(t / 2)
tensor([[0.5000, 1.0000],
        [1.5000, 2.0000]])

> print(t1.add(2))
tensor([[3., 4.],
        [5., 6.]])

> print(t1.sub(2))
tensor([[-1.,  0.],
        [ 1.,  2.]])

> print(t1.mul(2))
tensor([[2., 4.],
        [6., 8.]])

> print(t1.div(2))
tensor([[0.5000, 1.0000],
        [1.5000, 2.0000]])   

  这个看起来跟我们刚刚定义的 element-wise 运算有点冲突，我们刚讨论的是两个张量之间的运算，这里明明是一个标量和一个张量的运算。为什么也被视作是 element-wise 的运算呢？我们需要了解 PyTorch 中的 broadcast 机制。

  以 t1 + 2 为例，我们首先将标量 2 变换成 t1 的形状，然后再执行 element-wise 的操作，有点类似于 numpy 中的 broadcast_to() 函数。

> np.broadcast_to(2, t1.shape)
array([[2, 2],
        [2, 2]])

  所以，对于 t1 + 2 这个运算，实际上的过程为：

> t1 + torch.tensor(
    np.broadcast_to(2, t1.shape)
    ,dtype=torch.float32
)
tensor([[3., 4.],
        [5., 6.]])

  broadcast 机制还可以进一步推广，低秩张量和高秩张量之间也可以进行 element-wise 的运算。

> t1 = torch.tensor([
    [1, 1],
    [1, 1]
], dtype=torch.float32)

> t2 = torch.tensor([2, 4], dtype=torch.float32)

> np.broadcast_to(t2.numpy(), t1.shape)
array([[2., 4.],
       [2., 4.]], dtype=float32)

> t1 + t2
tensor([[3., 5.],
        [3., 5.]])

   低秩张量的每一个轴的元素个数要么和对应高秩张量轴的元素个数相等，要么元素数为1，才能顺利进行 broadcast 操作。

> t3 = torch.ones(3,3,2) # 高秩张量形状为(3,3,2)
> t3
tensor([[[1., 1.],
         [1., 1.],
         [1., 1.]],

        [[1., 1.],
         [1., 1.],
         [1., 1.]],

        [[1., 1.],
         [1., 1.],
         [1., 1.]]])

> t4 = torch.tensor([2,4],dtype=torch.float32) # 此时低秩张量形状为(2),满足条件
> t3 + t4
tensor([[[3., 5.],
         [3., 5.],
         [3., 5.]],

        [[3., 5.],
         [3., 5.],
         [3., 5.]],

        [[3., 5.],
         [3., 5.],
         [3., 5.]]])

> t5 = torch.tensor([[2, 4]],dtype=torch.float32) # 此时张量形状为(1,2),满足条件
> t3 + t5
tensor([[[3., 5.],
         [3., 5.],
         [3., 5.]],

        [[3., 5.],
         [3., 5.],
         [3., 5.]],
         
        [[3., 5.],
         [3., 5.],
         [3., 5.]]])

> t6 = torch.tensor([[2, 4],[1, 3]],dtype=torch.float32) # 张量形状为(2,2),不符条件
> t3 + t6 # 输出报错
RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1

> t7 = torch.tensor([[2, 4],[1, 3],[0, 5]],dtype=torch.float32) # 张量形状为(3,2),满足条件
> t3 + t7
tensor([[[3., 5.],
         [2., 4.],
         [1., 6.]],

        [[3., 5.],
         [2., 4.],
         [1., 6.]],

        [[3., 5.],
         [2., 4.],
         [1., 6.]]])

> t8 = torch.tensor([[[2, 4],[1, 3],[0, 5]]],dtype=torch.float32) # 张量形状为(1,3,2),满足条件
> t3 + t8
tensor([[[3., 5.],
         [2., 4.],
         [1., 6.]],

        [[3., 5.],
         [2., 4.],
         [1., 6.]],

        [[3., 5.],
         [2., 4.],
         [1., 6.]]])

  比较大小的操作也是 element-wise类型的，一个张量与某一个数值进行比较，返回的是一个和原始张量形状相同、取值为bool类型的张量。

> t = torch.tensor([[0,5,0],[6,0,7],[0,8,0]], dtype=torch.float32)

> t.eq(0)
tensor([[ True, False,  True],
        [False,  True, False],
        [ True, False,  True]])

> t.eq(0).dtype
torch.bool

> t.ge(0)
tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])

> t.gt(0)
tensor([[False,  True, False],
        [ True, False,  True],
        [False,  True, False]])

> t.le(0)
tensor([[ True, False,  True],
        [False,  True, False],
        [ True, False,  True]])

> t.lt(0)
tensor([[False, False, False],
        [False, False, False],
        [False, False, False]])

  PyTorch中内置的 element-wise 类型的函数：

> t = torch.tensor([[1,-2,3],[-4,5,-6],[7,-8,9]],dtype=torch.float32)
> t
tensor([[ 1., -2.,  3.],
        [-4.,  5., -6.],
        [ 7., -8.,  9.]])
        
> t.abs()
tensor([[1., 2., 3.],
        [4., 5., 6.],
        [7., 8., 9.]])
        
> t.abs().sqrt()
tensor([[1.0000, 1.4142, 1.7321],
        [2.0000, 2.2361, 2.4495],
        [2.6458, 2.8284, 3.0000]])

> t.neg()
tensor([[-1.,  2., -3.],
        [ 4., -5.,  6.],
        [-7.,  8., -9.]])

  最后说一下，以下词语名称不同，但是都代表着 element-wise 类型的操作：

• element-wise
• component-wise
• point-wise

12. reduction操作

  reduction 操作指的是减少某个张量中元素个数的操作，我们前面提过的 reshape 和 element-wise 操作都不会改变张量中的元素个数，我们通过示例来看：

t = torch.tensor([[0,1,0],[2,0,2],[0,3,0]],dtype=torch.float32)
>>> t
tensor([[0., 1., 0.],
        [2., 0., 2.],
        [0., 3., 0.]])

> t.sum() # 输出张量元素个数为1
tensor(8.)

> t.numel() # num of element的缩写
9
>>> type(t.numel())
<class 'int'>

> t.prod()
tensor(0.)

> t.mean()
tensor(0.8889)

> t.std()
tensor(1.1667)

  并不是只把元素个数缩减为1的操作，叫做 reduction ops，下面的操作也是：

> t = torch.tensor([[1,1,1,1],[2,2,2,2],[3,3,3,3]],dtype=torch.float32)
> t
tensor([[1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])
> t.shape
torch.Size([3, 4])

> t.sum(dim=0)
tensor([6., 6., 6., 6.])

> t.sum(dim=1)
tensor([ 4.,  8., 12.])

  如何理解 dim=0 和 dim=1 所得的两种不同的结果呢？

> t.sum(dim=0) 
> 可以理解为其他轴的索引保持不变，只改变第一个轴的元素索引值，如下所示
t[0][0] + t[1][0] + t[2][0] 
t[0][1] + t[1][1] + t[2][1] 
t[0][2] + t[1][2] + t[2][2]
t[0][3] + t[1][3] + t[2][3]

> t.sum(dim=1) 
> 可以理解为其他轴的索引保持不变，只改变第二个轴的元素索引值，如下所示
t[0][0] + t[0][1] + t[0][2] + t[0][3]
t[1][0] + t[1][1] + t[1][2] + t[1][3]
t[2][0] + t[2][1] + t[2][2] + t[2][3]

  另外一种常见的 reduction 操作是 argmax()，作用是返回张量中最大元素值的索引，我们举例说明：

> t = torch.tensor([
    [1,0,0,2],
    [0,3,3,0],
    [4,0,0,5]], dtype=torch.float32)

> t.max()
tensor(5.)

> t.argmax()
tensor(11)

> t.flatten()
tensor([1., 0., 0., 2., 0., 3., 3., 0., 4., 0., 0., 5.])

  我们还可以指定轴，返回轴上每个张量的最值。

> t.max(dim=0)
torch.return_types.max(values=tensor([4., 3., 3., 5.]),indices=tensor([2, 1, 1, 2]))

> t.argmax(dim=0)
tensor([2, 1, 1, 2])

> t.max(dim=1)
torch.return_types.max(values=tensor([2., 3., 5.]),indices=tensor([3, 2, 3]))

> t.argmax(dim=1)
tensor([3, 2, 3])

  这里 dim=0 和 dim=1的作用和上面讨论的 sum() 是一致的，不再赘述。

  最后我们再来聊聊如何访问一个张量中的内部元素：

> t = torch.tensor([
    [1,2,3],
    [4,5,6],
    [7,8,9]], dtype=torch.float32)

> t.mean()
tensor(5.)

> t.mean().item() # item() 适用于标量
5.0

> t.mean(dim=0).tolist() # 返回 Python list 类型
[4.0, 5.0, 6.0]

> t.mean(dim=0).numpy() # 返回 ndarray 类型
array([4., 5., 6.], dtype=float32)

  到现在为止，我们已经对 PyTorch 的张量有一个基础的认识，我们现在对张量的使用还仅处于一个非常原始的阶段，在一个篇章，我们将结合 Fashion Mnist 数据集来进一步挖掘 PyTorch 的强大之处。