证据近似
在前面章节已经讲到在处理线性基函数的贝叶斯方法中,通过引入超参α、β的先验分布,通过对超参以及w求积分做预测。这种方法只能对ω的积分或对超参积分,但对所有变量的求积分是没有解析解的。这里提出证据近似的方法。
这种方法:首先为ω求积分,得到边缘似然函数,通过最大化边缘似然函数,确定超参的值。
假设引入α、β的超先验分布,预测分布则可通过ω、α、β求积分得到:
假设后验分布p(α,β|t)在α、β附近有尖峰,则α、β则被固定,即:

3.5.1 计算证据函数
边缘似然函数p(t|α,β)通过对ω积分得到:

计算这个积分有两种方法:1.使用线性-高斯模型的条件概率分布结果;2.通过对指数项配平方,使用高斯分布的归一化。
我们得到证据函数:
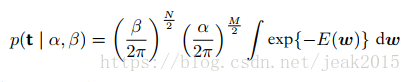
同时还定义了:
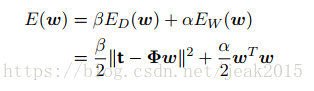





 本文介绍了PRML中证据近似的方法,用于处理无法直接求解所有变量积分的问题。通过最大化边缘似然函数来确定超参数的值。详细讨论了计算证据函数的两种方法,以及如何对α和β求导以找到它们的最优值。最后提到了参数的有效数量,但由于作者未深入理解,这部分内容有待进一步学习和分享。
本文介绍了PRML中证据近似的方法,用于处理无法直接求解所有变量积分的问题。通过最大化边缘似然函数来确定超参数的值。详细讨论了计算证据函数的两种方法,以及如何对α和β求导以找到它们的最优值。最后提到了参数的有效数量,但由于作者未深入理解,这部分内容有待进一步学习和分享。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 846
846

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








