PRML阅读笔记（三）

CH3 Linear models for regression回归的线性模型

3.1线性基函数模型

• 回归的最简单模型
  $$y(\mathbf{x},\mathbf{w})=w_0+w_1{x}_1+\dots +w_D{x}_D$$
  其中$\mathbf{x}=(x_1,\dots ,x_D{)}^T$.

• 扩展模型

  将输入变量的固定的非线性函数进行线性组合

  形式为
  $$y(\mathbf{x},\mathbf{w})=w_0+\sum _{j=1}^{M-1}{w}_j{\varphi }_j(\mathbf{x})$$
  其中${\varphi }_j(\mathbf{x})$称为基函数（basis function）。此模型中的参数总数为$M$。参数$w_0$称为偏置参数（bias parameter）

  定义${\varphi }_0(\mathbf{x})=1$,此时
  $$y(\mathbf{x},\mathbf{w})=\sum _{j=0}^{M-1}{w}_j{\varphi }_j(\mathbf{x})={\mathbf{w}}^T\varphi (\mathbf{x})$$
  其中$\mathbf{w}=(w_0,\dots ,w_M-1{)}^T$且$\varphi =({\varphi }_0,\dots ,{\varphi }_{M-1}{)}^T$。基函数{ ${\varphi }_j(\mathbf{x})$}可以表示原始变量$\mathbf{x}$的特征（预处理或特征抽取后的）

• 基函数选择

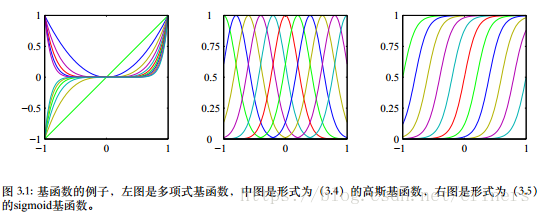
  多项式拟合，基函数：${\varphi }_j(x)=x^j$。局限性：是输入变量的全局函数，因此对于输入空间一个区域的改变将会影响所有其他的区域。解决：把输入空间切分成若干个区域，对每个区域用不同的多项式函数拟合。----样条函数（spline function）？？?

  高斯基函数，${\varphi }_j(x)=\exp \left\{-\frac{(x-{\mu }_j{)}^2}{2s^2}\right\}$,其中${\mu }_j$控制了基函数在输入空间中的位置，参数$s$控制了基函数的空间大小。未必是一个概率表达式。归一化系数不重要，因为有调节参数$w_j$

  sigmoid基函数，${\varphi }_j(x)=\sigma (\frac{x-{\mu }_j}{s})$,其中$\sigma (a)=\frac{1}{1+\exp (-a)}$是logistic sigmoid函数。等价地可以使用tanh函数，和logistic sigmoid函数的关系为tanh($a$)=$2\sigma (2a)-1$

  傅里叶基函数，用正弦函数展开。

3.1.1最大似然与最小平方

假设目标变量$t$由确定的函数$y(\mathbf{x},\mathbf{w})$给出，附加高斯噪声，即
$$t=y(\mathbf{x},\mathbf{w})+ϵ$$
其中$ϵ$是一个零均值的高斯随机变量，精度为$\beta$，有
$$p(t|\mathbf{x},\mathbf{w},\beta )=\mathcal{N}(t|y(\mathbf{x},\mathbf{w}),{\beta }^{-1})$$

ch1中，假设一个平方损失函数，对于$\mathbf{x}$的一个新值，最优预测由目标变量的条件均值给出，在高斯条件分布的情况下，条件均值可写成
$$\mathbb{E}[t|\mathbf{x}]=\int tp(t|\mathbf{x})dt=y(\mathbf{x},\mathbf{w})$$
高斯噪声的假设表明，给定$\mathbf{x}$的条件下，$t$的条件分布是单峰的，可以扩展到条件高斯分布的混合，描述多峰的条件分布

考虑一个输入数据集X={ x1,…,xN}\boldsymbol X=\left\{\boldsymbol x_1,\ldots,\boldsymbol x_N\right\}X={ x1​,…,xN​}，对应的的目标值为$t_1,\dots ,t_N$，将目标向量{ $t_n$}组成一个列向量，记作$\mathbf{t}$。假设数据点独立，得到似然函数为
$$p(\mathbf{t}|\mathbf{X},\mathbf{w},\beta )=\prod _{n=1}^N\mathcal{N}(t_n|{\mathbf{w}}^T\varphi ({\mathbf{x}}_n),{\beta }^{-1})$$
取对数似然函数，有(不显式地写出$\mathbf{x}$)
$$\ln p(\mathbf{t}|\mathbf{w},\beta )=\sum _{n=1}^N\ln \mathcal{N}(t_n|{\mathbf{w}}^T\varphi ({\mathbf{x}}_n),{\beta }^{-1})=\frac{N}{2}\ln \beta -\frac{N}{2}\ln (2\pi )-\beta E_D(\mathbf{w})$$
其中平方和误差函数为
$$E_D(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N{\left\{t_n-{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)\right\}}^2$$
对数似然函数的梯度为
$$\nabla \ln p(\mathbf{t}|\mathbf{w},\beta )=\beta \sum _{n=1}^N\left\{t_n-{\mathbf{w}}^T\varphi ({\mathbf{x}}_n)\right\}\varphi ({\mathbf{x}}_n{)}^T$$
令梯度为0，得
$$0=\sum _{n=1}^N{t}_n\varphi ({\mathbf{x}}_n{)}^T-{\mathbf{w}}^T(\sum _{n=1}^N\varphi ({\mathbf{x}}_n)\varphi ({\mathbf{x}}_n{)}^T)$$
求解$\mathbf{w}$，有
$${\mathbf{w}}_{ML}=({\mathbf{\Phi }}^T\mathbf{\Phi }{)}^{-1}{\mathbf{\Phi }}^T\mathbf{t}$$
称为最小平方问题的规范方程（normal equation），$\mathbf{\Phi }$是$N\times M$的矩阵，称为设计矩阵（design matrix），元素为${\Phi }_{nj}={\varphi }_j({\mathbf{x}}_n)$,即
$$\mathbf{\Phi }=\left(\begin{array}{cccc}{\varphi }_0({\mathbf{x}}_1)& {\varphi }_1({\mathbf{x}}_1)& \cdots & {\varphi }_{M-1}({\mathbf{x}}_1)\\ {\varphi }_0({\mathbf{x}}_2)& {\varphi }_1({\mathbf{x}}_2)& \cdots & {\varphi }_{M-1}({\mathbf{x}}_2)\\ ⋮& ⋮& \ddots & ⋮\\ {\varphi }_0({\mathbf{x}}_N)& {\varphi }_1({\mathbf{x}}_N)& \cdots & {\varphi }_{M-1}({\mathbf{x}}_N)\end{array}\right)$$
量
$${\mathbf{\Phi }}^{†}\equiv ({\mathbf{\Phi }}^T\mathbf{\Phi }{)}^{-1}{\mathbf{\Phi }}^T$$
成为矩阵的Moore-Penrose伪逆矩阵（pseudo-inverse matrix），可被看成逆矩阵的概念对于非方阵的矩阵的推广

显式地写出偏置参数，误差函数为
$$E_D(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N{\left\{t_n-w_0-\sum _{j=1}^{M-1}{w}_j{\varphi }_j(x_n)\right\}}^2$$
令关于$w_o$的导数等于零，解出$w_o$，得
$$w_0=\bar{t}-\sum _{j=1}^{M-1}{w}_j{\bar{\varphi }}_j$$
其中定义了
$$\bar{t}=\frac{1}{N}\sum _{n=1}^N{t}_n$$

$${\bar{\varphi }}_j=\frac{1}{N}\sum _{n=1}^N{\varphi }_j({\mathbf{x}}_n)$$

因此偏置$w_0$补偿了目标值的平均值（在训练集上的）与基函数的值的平均值的加权求和之间的差。

关于噪声精度参数$\beta$最大化似然函数
$$\frac{1}{{\beta }_{ML}}=\frac{1}{N}\sum _{n=1}^N{\left\{t_n-w_{ML}^T\varphi (x_n)\right\}}^2$$
因此噪声精度的倒数由目标值在回归函数周围的残留方差给出

3.1.2最小平方的几何描述

考虑一个$N$维空间，坐标轴由$t_n$给出，$\mathbf{t}=(t_1,\dots ,t_N)$是空间中的一个向量 ，每个在$N$个数据点处估计的基函数${\varphi }_j({\mathbf{x}}_n)$可以表示为这个空间中的一个向量，记作${\phi }_j$,对应于$\Phi$的第$i$列

如果基函数的数量$M$小于数据点的数量$N$，那么$M$个向量${\phi }_j$将会张成一个$M$维的子空间$S$。

定义$\mathbf{y}$是一个$N$维向量，第$n$个元素为$y({\mathbf{x}}_n,\mathbf{w})$,由于$\mathbf{y}$是向量φj\varphi_j