【理论+实操】GeoDa空间自相关

🍉优快云小墨&晓末:https://blog.youkuaiyun.com/jd1813346972

   个人介绍: 研一｜统计学｜干货分享
         擅长Python、Matlab、R等主流编程软件
         累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

该篇文章以某市各区县净流动人口为例，实例操作某次人口普查该数据的空间自相关和局部空间自相关情况。例如其它变量空间相关分析，双变量的空间自相关分析可模仿相关操作，包括空间自相关相关原理；.shp数据与研究变量数据的合并；全局莫兰指数；莫兰散点图，冷热地区LISA图等。

创作不易，望互动收藏！若有不足，敬请指正！

1 空间自相关原理

1.1 全局空间自相关

  全局空间自相关用于分析和研究整个区域的空间依赖模式，用一个数值来反应全局的空间相关模式。常用于度量全局空间自相关的指标为全局Moran 统计量。全局Moran 统计量测度空间分布的各区县研究变量水平高、低的相似程度，用来反映各区县该变量的聚集程度。

  全局Moran 统计量计算公式:

$$I=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}(x_i-\bar{x}(x_j-\bar{x}))}{S^2{\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}}$$

  其中，指数I 为全局Moran 统计量，也记为Global Moran’s I 指数，n 为样本总数，$x_i(x_j)$为重庆第$i(j)$个区县的变量值，$\bar{x}$为各区县该研究变量的均值。$S^2=\frac{1}{n}{\sum }_{i=1}^n\bar{x}$为各区县研究变量的方差，$w_{ij}$反映相邻区县邻近关系的二元变量，即邻近为1，不邻近为0。I 的取值范围在［－ 1，1］之间，大于0 表示正相关，小于0表示负相关，等于0 不相关; 对于全局Moran 指数，可以构造服从正态分布的统计量Z，采用双侧检验法来判断n 个区域是否具有显著空间自相关关系。Z 统计量计算公式: $Z=\frac{I-E(I)}{\sqrt{Var(I)}}$。式中I 为Moran’s I 统计量;$E(I)$为Moran’s I 的期望值; $VAR(I)$ 为Moran’s I 的方差。在给定显著性水平下，当Z 值为正且显著时，表示相似研究变量在空间内聚集。当Z 值为负且显著时，表明相似研究变量在空间内趋于分散分布; 当Z 值为0 时，表明各区县相似研究变量之间呈现随机分布，并无空间相关性。

1.2 局部空间自相关

  局部空间自相关方法用于探究一个区县和其相邻的区县在研究变量上的空间差异程度及显著性，常用局部Moran’s I 统计量进行测度，并结合Moran 散点图和LISA 集聚图对我国危险废弃物产生量的局部空间分布进行研究。局部Moran’s I 统计量定义如下形式:

$I_i=Z_i{\sum }_{j=1}^n{w}_{ij}{Z}_j$

  其中，$Z_j$与$Z_j$为第ｉ、第ｊ个区县研究变量与均值的偏差，即$Z_i=(X_i-\bar{x})$，$Z_j=(X_j-\bar{x})$。其中$w_{ij}$为标准化的空间权重矩阵，其对角线元素全为0。在给定显著性水平下，$I_i$＞ 0 说明存在正相关，相邻区县相似值聚集; $I_i$< 0 说明存在负相关，相邻区县不相似值聚集。局部Moran’s I 统计量也需要显著性检验，P 值同样为零假设$H_0$检验提供判断，检验所有的研究变量在局部空间上的分布是否具有随机性。

1.3 莫兰散点图

  Moran 散点图刻画出了各区县研究变量与其空间滞后项之间的关系，并对其进行了可视化二维展示，反映考察变量在局部地区范围内的空间自相关性。在散点图中，四个象限分别被划分成高—高、低—低、高—低、低—高四种类型。其中落入高—高( 或低—低) 区域的点具有较高( 低) 的研究变量值，且其相邻区域也具有较高( 低) 的研究变量值，属于空间正相关; 落入高—低以及低—高区域中的点属于空间负相关，前者表示研究变量值较高的区县被研究变量值较低的区县包围，后者表示研究变量值较低的区县被研究变量值较低的区县包围。结合LISA 显著性水平和Moran 散点图，形成LISA 集聚图。它可以识别研究变量值在局部空间的“冷点”和“热点”地区，揭示空间异质现象。

2 项目实操

2.1 项目背景

  以某市各区县净流动人口为例，实例操作某次人口普查该数据的空间自相关和局部空间自相关情况。

2.2 实操步骤

2.2.1 地理数据导入

  打开GeoDa软件，导入对应地理信息文件（.shp格式）。

2.2.2 地理信息文件和研究变量的合并

  1.数据集合并，点击Table后点击Merge Table Data。

GeoDa可直接将地理信息文件数据和研究变量合并。

  2.导入各区县净流入人口数据，.csv格式。

  3.根据实际情况合并数据集，此处演示使用关键词匹配，即shp文件中的关键词name，和净流入人口数据集中的name，然后选中需要合并的变量移到从“Excude”移动到Include。

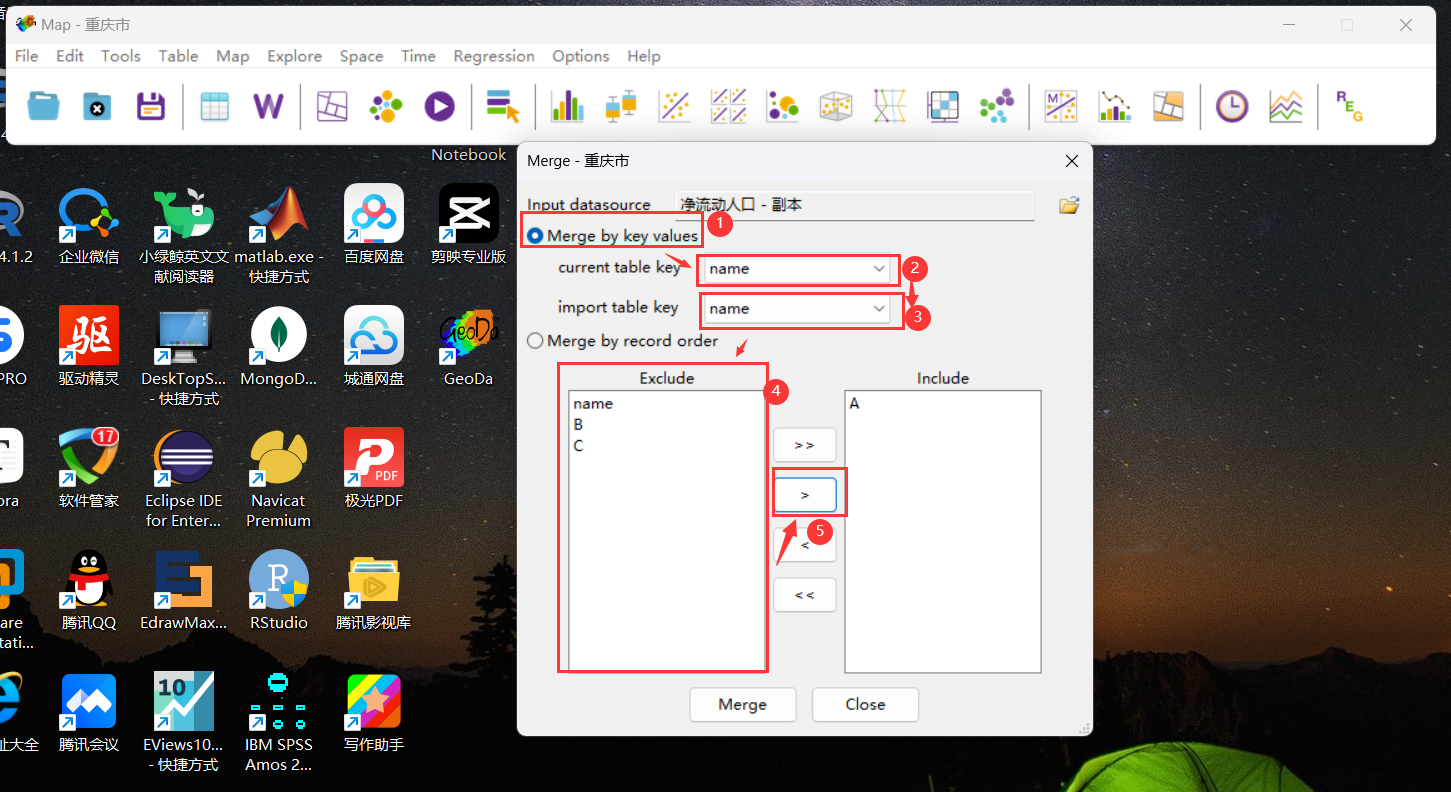
  合并后数据情况，红色列为原始shp数据上新增数据列。

2.2.3 创建邻接矩阵

  创建邻接矩阵：按图示依次点击会生成一个邻接矩阵文件(.gal格式)。

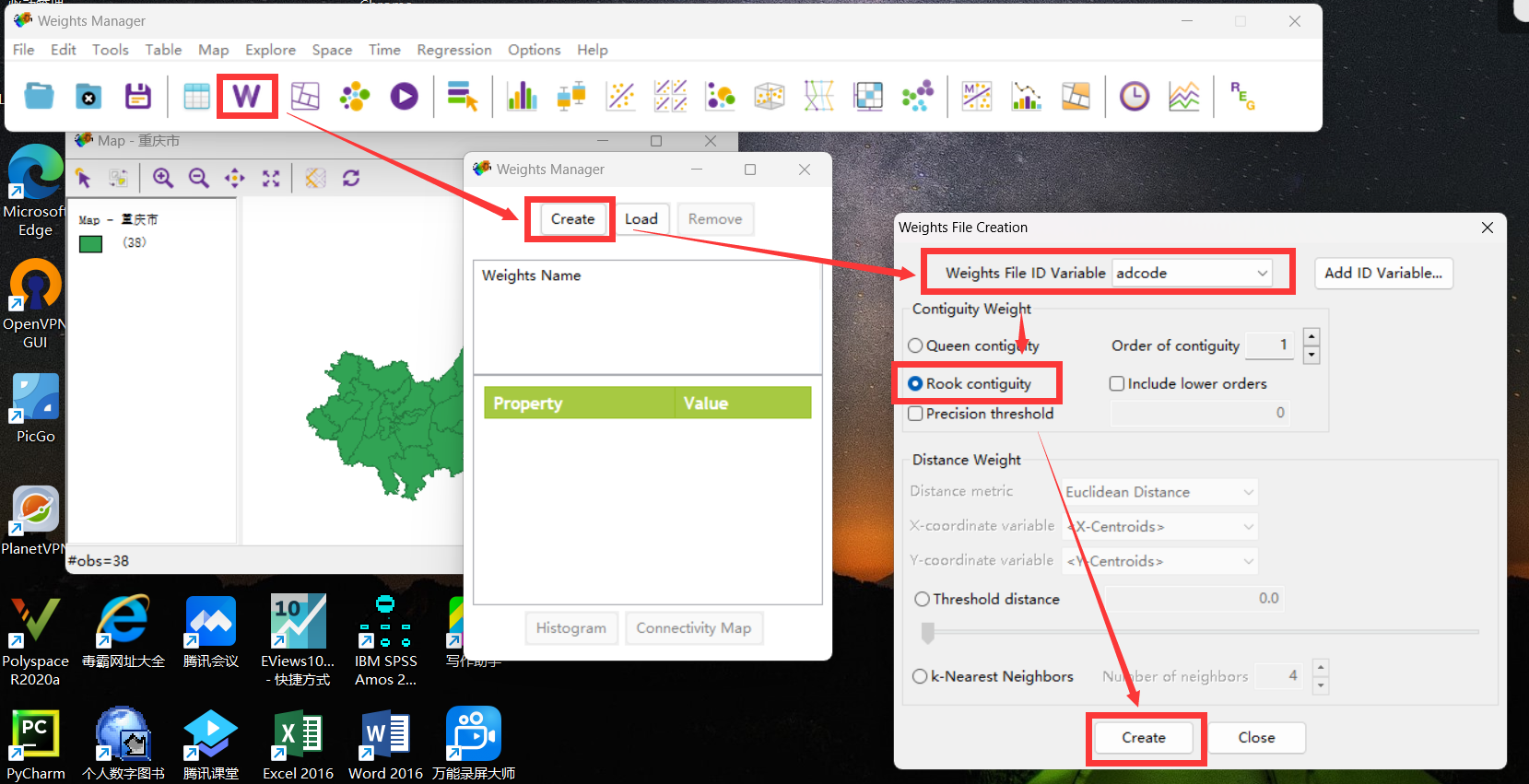
结合实际情况生成邻接矩阵，本次演示使用Rook邻接方式。

2.2.4 全局空间自相关

  1.全局空间自相关相关结果输出：点击Space的单变量莫兰指数，然后选中研究变量，点击“OK”。

  2.显著性水平展示：在莫兰散点图上点击鼠标右键，选中随机化，一般选中999次。

  图中选中的三个值是在全局自相关分析中需要着重注意的三个值，分别为全局莫兰指数；显著性p值，检验统计量z值。

2.2.5 局部空间自相关

  8.局部空间自相关相关结果输出：点击Space的单变量局部指数，然后选中研究变量，点击“OK”，然后继续点击“OK”（弹窗内默认选中了显著性地图；聚类地图；莫兰散点图）。

小Tip:打开数据表，选中地图或散点图中目标区域，对应区域在数据表中会高亮显示，便于查看。