Binary Cross Entropy Loss
二进制交叉熵损失函数是分类中非常经典的一种loss,其计算公式如下:
L
B
C
E
=
−
y
l
o
g
(
y
′
)
−
(
1
−
y
)
l
o
g
(
1
−
y
′
)
L_{BCE}=-y log(y')-(1-y)log(1-y')
LBCE=−ylog(y′)−(1−y)log(1−y′)
其中y表示某个类别上的GT(值为0或1),y‘表示经过神经网络预测得到的对应类别的置信度(因为做过softmax处理,所以值在(0,1)之间)。当y=0时,上式中只有第二项,此时y‘越接近于0,则loss越小;当y=1时,上式只有第一项有值,此时y’越接近于1,则loss越小。
Cross Entropy Loss
和BCE LOSS有一些不同,BCE Loss输出只有一个[0,1]的结点;而CE可以做多分类,其损失函数表达如下:
L C E = − ∑ i p i l o g p i ^ L_{CE}=-\sum_{i} p_{i}log\hat{p_{i}} LCE=−i∑pilogpi^
其中,p表示GT, p ^ \hat{p} p^表示预测值。i的数目表示类别总数。眼尖的你可能会发现,这个式子只在GT为1的时候有值,那GT为0的时候岂不丢失了这部分损失,无法让小的值向0收敛。其实是这样的,CE之前通常用softmax,这样所有的 p ^ i \hat{p}_{i} p^i之和等于1,而且大的更大,小的更小。所以让GT为1的类别更加接近1,隐式地让GT为0的那些类别的预测接近于0.
L1/L2 Loss
坐标或者wh回归时常用的loss,计算式分别如下:
L 1 = ∣ y ′ − y ∣ L_{1}=|y'-y| L1=∣y′−y∣
L 2 = ∣ y ′ − y ∣ 2 L_{2}=|y'-y|^{2} L2=∣y′−y∣2
其中y表示GT值(物理含义可以表示object的坐标,bbox宽高等),y’表示经神经网络的预测值(一般也是预测bbox的位置、宽高等信息)。该函数的目的就是minimize预测值与GT之间的L1/L2距离。
smooth L1 Loss
smooth-L1在L1 loss的基础上做出一点改动,使得Loss在定义域内处处可导,其公式定义如下:
L s m o o t h _ L 1 = { 0.5 x 2 , ∣ x ∣ < 1 ∣ x ∣ − 0.5 , ∣ x ∣ ≥ 1 L_{smooth\_L1}= \begin{cases} 0.5x^{2}, |x|<1 \\ |x|-0.5, |x|\ge1 \end{cases} Lsmooth_L1={0.5x2,∣x∣<1∣x∣−0.5,∣x∣≥1
上式中的x就是L1 Loss中的|y’-y|,smooth L1 loss是在Faster RCNN中提出的,可以看下它和L2 loss的对比:
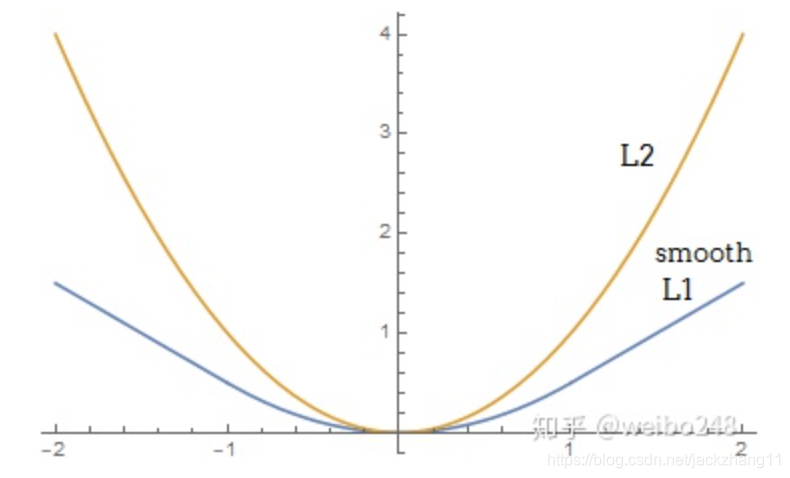
可以看出smooth L1在一些离群点上梯度也只是1,不会像L2 Loss一样梯度会很大。因此可以说smooth l1 loss对离群点和异常点更加鲁棒。
Huber Loss
Huber Loss也是常用的回归loss之一,可以看作是上述smooth L1 Loss的拓展,其计算式如下:
L s m o o t h _ L 1 = { 0.5 x 2 , ∣ x ∣ ≤ δ δ ∣ x ∣ − 0.5 δ 2 , o t h e r w i s e L_{smooth\_L1}= \begin{cases} 0.5x^{2}, |x|\le \delta \\ \delta|x|-0.5\delta ^{2}, otherwise \end{cases} Lsmooth_L1={0.5x2,∣x∣≤δδ∣x∣−0.5δ2,otherwise
根据上面的公式可以看出,smooth l1是在
δ
=
1
\delta=1
δ=1时的一种特例。那么为什么要引入这个loss呢?可以发现,当
δ
→
0
\delta \rarr0
δ→0时,损失函数接近MAE;当
δ
→
∞
\delta \rarr \infty
δ→∞时,损失函数接近MSE。随着
δ
\delta
δ的变化,整个loss曲线的变化可以参考一下下图:
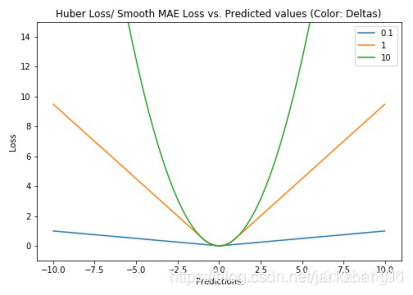
可以看出,MSE的情况对于离群点太敏感,鲁棒性可能不好;MAE整体太平缓,可能会出现梯度弥散。所以Huber Loss采取了一个折衷的方法,通过合理调节超参数
δ
\delta
δ,在消除离群点敏感的影响同时,也能保证一定的梯度,同时该loss在定义域内处处可导。当
δ
=
1
\delta=1
δ=1时,Huber loss可以看作是smooth L1 Loss。
IoU Loss
IoU Loss也是一个跟检测框相关的回归loss。之前有L2 Loss可以计算预测bbox的位置宽高与GT之间的距离,并没有考虑坐标间的相关性。而IoU Loss则是从box的角度出发,具备位置的相关性,如下图所示:
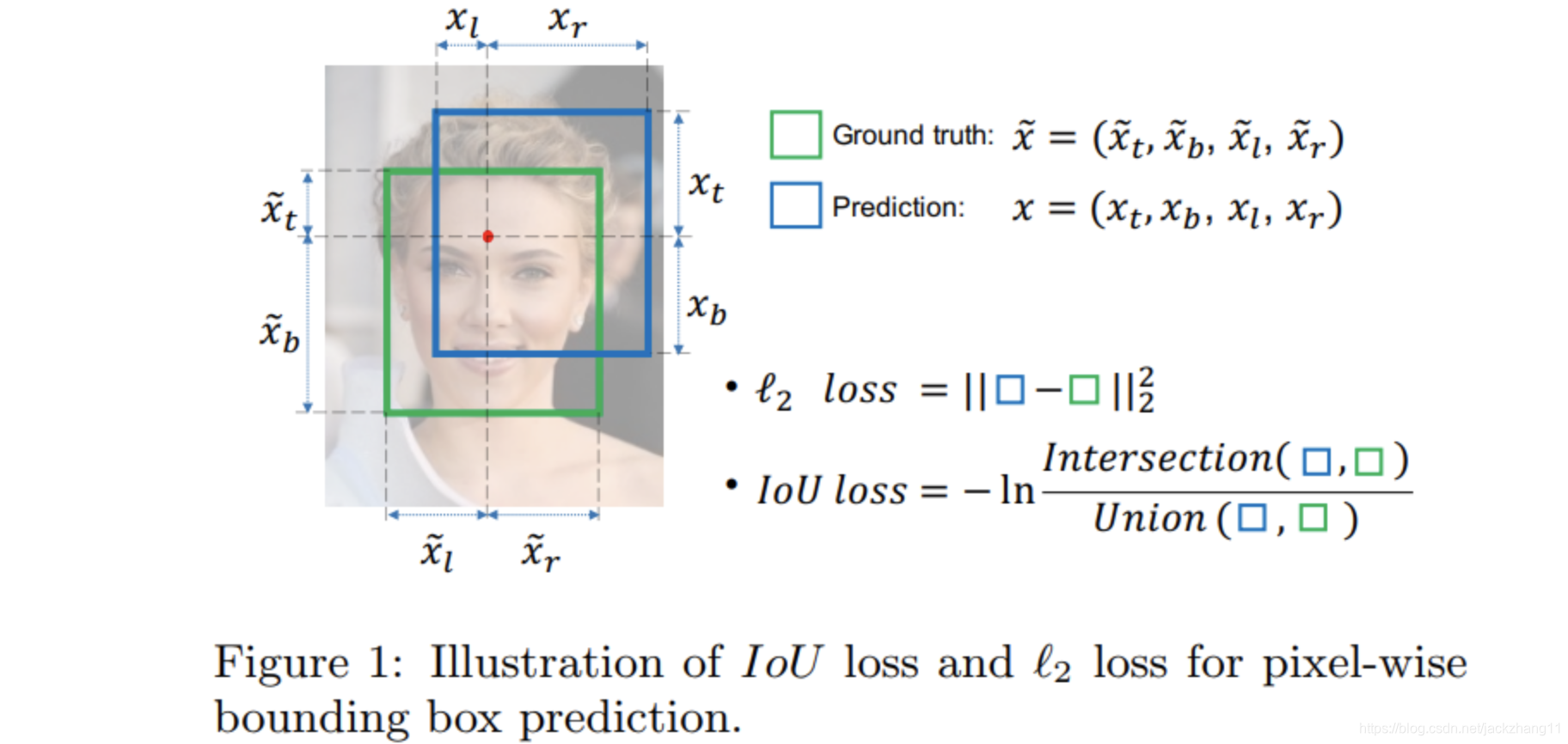
IoU Loss在做检测框回归方面要更胜L2 Loss一筹,当两个box的IoU=1时,此时IoU Loss最小为1;当两个box的IoU很小,趋近于0时,此时的IoU Loss会非常大。
GIoU/DIoU/CIoU Loss
显而易见,IoU Loss在两个框没有交集IoU=0时,无法衡量两者之间的距离(相邻不重叠的,和相隔天涯海角的box之间的IoU是一样的);并且IoU Loss无法精确反映两个box之间的重合度大小。因此就有了后续若干个IoU Loss的改进版,这里篇幅所限不讨论了,可以参照这篇博客。
Focal Loss
Focal Loss是目前在检测领域应用非常广泛的分类loss。由于在detection任务中正负样本的不均衡,并且存在难易样本(接近GT的样本为易分样本,离GT较远的称为难分样本)。所以需要利用Focal Loss解决这两个问题。
我们可以从传统的交叉上损失函数出发:

为了解决正负样本不均衡的问题,可以引入一个参数
α
\alpha
α,来给正样本loss更大的权重,如下:

加入
α
\alpha
α以后解决了正负样本不均衡的问题,但是并没有解决难易样本的问题。作者认为,易分样本对于模型精度的提升效果很小,模型应该更多的关注那些难分样本。所以这里的处理方法就是,将高置信度(易分)样本的损失降低一些,或者将低置信度(难分)样本的损失提高一些。所以就有了如下公式:

举个栗子,当
γ
=
2
,
p
=
0.968
\gamma=2, p=0.968
γ=2,p=0.968时,
(
1
−
p
)
γ
=
0.001
(1-p)^ \gamma=0.001
(1−p)γ=0.001,此时就相当于把这个置信度很大的易分样本的权重削弱了1000倍。Focal Loss的最终表达形式如下所示:

实验证明当
γ
=
2
,
α
=
0.25
\gamma=2, \alpha=0.25
γ=2,α=0.25时,效果最佳。
去年NeurIPS20上又出现了Focal Loss的改进版GFocal Loss,感兴趣的可以看下这篇文章。
Dice Loss
Dice Loss在分割中有着广泛的应用,用于计算预测mask和GT mask之间的差别,这个loss需要从Dice系数说起。
Dice系数: s = 2 ∣ X ∩ Y ∣ ∣ X ∣ + ∣ Y ∣ s=\frac{2|X\cap Y|}{|X|+|Y|} s=∣X∣+∣Y∣2∣X∩Y∣,其中X表示GT mask,Y表示预测得到的mask。两个mask都是和原图像大小,且每个位置非0即1的掩膜。之所以分子上乘2,是因为分母存在重复加的情况。我们发现,当X与Y完全一样时,s=1;当X与Y完全不重叠时,s=0。因此整个Dice系数的取值在[0, 1]。
Dice系数用更一般的表示方法可以表达为: s = 2 T P 2 T P + F N + F P s=\frac{2TP}{2TP+FN+FP} s=2TP+FN+FP2TP。这个公式可以完美的和上面的对应,TP就是预测mask和GT mask对应点都为1的部分;FN是预测mask为0 而GT mask为1的部分;FP是预测mask为1 而GT mask为0的部分。所以这个形式是Dice系数的更普遍的表达。
Dice Loss的计算式如下:
L D i c e = 1 − 2 ∣ X ∩ Y ∣ ∣ X ∣ + ∣ Y ∣ L_{Dice}=1-\frac{2|X\cap Y|}{|X|+|Y|} LDice=1−∣X∣+∣Y∣2∣X∩Y∣
但是Dice Loss在训练误差曲线会比较混乱,偶尔也会出现一些极端情况导致训练的不稳定,关于Dice Loss存在的一些问题,可以参考这篇文章。
Dice Loss是Tversky Loss一种特殊形式,有兴趣的小伙伴可以读一下Tversky Loss的论文。
Hinge Loss
之前在一篇embedding clustering类型的实例分割论文中看到过这个loss(《Instance Segmentation by Jointly Optimizing Spatial Embeddings and
Clustering Bandwidth》)。这个loss最早应该出现在SVM中,其主要的思想是给出一个松弛margin。众所周知,前面的所有loss,只要预测值和GT之间有一点的差别,loss就不会为0。而这个Loss的精髓之处就是,给定一个松弛空间,在离GT很近(小于margin)的这部分空间中,loss的计算值也设置为0。因此Hinge Loss的计算式可以概括如下:
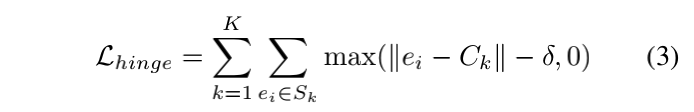
这里截取了上述论文中的Hinge loss的公式,主要解释一下思想:
C
k
C_{k}
Ck表示第k个实例的质心,
e
i
e_{i}
ei表示属于这个instance的某个pixel的位置。只要两者之间的距离不超过
δ
\delta
δ,整个loss的计算值就为0。所以
δ
\delta
δ在这里是一个松弛变量,容许估计值与GT有margin之内的误差,该误差不计算在loss之内。
Triplet Loss
做Tracking时常用的loss,因为tracking需要把前后两帧里相同的instance进行匹配,匹配的原则大多是基于embedding的相似度。所以为了学习到更精确的embedding,通常会在ReId网络中采用Triplet Loss。这个损失函数的具体细节不展开了,感兴趣的小伙伴可以阅读这篇博客,写得非常清晰。
欢迎小伙伴进行指正和补充。







 本文详细介绍了机器学习中常见的损失函数,包括二进制交叉熵损失、交叉熵损失、L1/L2损失等,并探讨了它们在不同场景下的应用,如分类、回归和目标检测等任务。
本文详细介绍了机器学习中常见的损失函数,包括二进制交叉熵损失、交叉熵损失、L1/L2损失等,并探讨了它们在不同场景下的应用,如分类、回归和目标检测等任务。
















 4190
4190










