变分自编码器VAE学习笔记

最近在看变分自编码器VAE的理论，一开始也是云里雾里。现在终于稍稍理清了一些思路，在这里分享一下。由于对这个领域的学识不深，不当之处请指正。

假如现在你想对 mnist 数据集进行建模，其中 $x$ 表示一张图像，p(x) 对应每一个 $x$ 可能存在的状态。由于数据非常繁复，想要直接求出这个概率密度 $p(x)$ 并不现实。因此，我们引入一个隐变量 $z$ 来描述处在某个流形中的 $x$ 的背景信息，如：有没有圈，有没有直的笔划等特性。所以，VAE的开始是基于下图的：

对于这个两层有向的概率图模型，$z$表示隐变量，$x$表示观测变量。$p(z)$是隐变量的先验概率，$p(x|z)$是$x$相对于$z$的条件概率，$p(z|x)$是隐变量的后验概率，这个概率图模型相当于解码器decoder（也可以说是生成器）。

因此，可以通过条件概率公式，以及联合分布与边缘密度的定义，将我们希望得到的概率$p(x)$进行转化：

$$p_{\theta }(x)={\int }_z{p}_{\theta }(x,z)dz={\int }_z{p}_{\theta }(x|z)p_{\theta }(z)dz（1）$$

假设$p(z)$是一个简单的高斯分布，$p(x|z)$是一个神经网络搭建的解码器。我们的目标是通过这个观测集$X$，来估计这个概率图模型的参数$\theta$。因此，需要最大化似然函数来估计模型的参数。但是对于 (1) 式，计算每一个$z$对应的$p(x|z)$不容易，所以似然函数$p(x)$无法直接用积分计算，必须进行转化。

我们再看看还有哪些量没有用到，发现 (1) 式中没有使用隐变量$z$的后验概率，根据贝叶斯公式，后验可表达如下：

$$p(z|x)=\frac{p(z)p(x|z)}{p(x)}（2）$$

但是对于 (2) 式等号右边的分母，我们是无从下手的，因此无法直接进行优化。

这时候VAE中经典的一步出现了：既然我们无法求得后验，那么直接定义一个编码器(encoder)网络$q_{\varphi }(z|x)$，将输入$x$编码为$z$，让$q_{\varphi }(z|x)$与后验$p(z|x)$接近，从而通过这个额外定义的网络来估计$z$的后验。我们假定整个模型是一个神经网络。

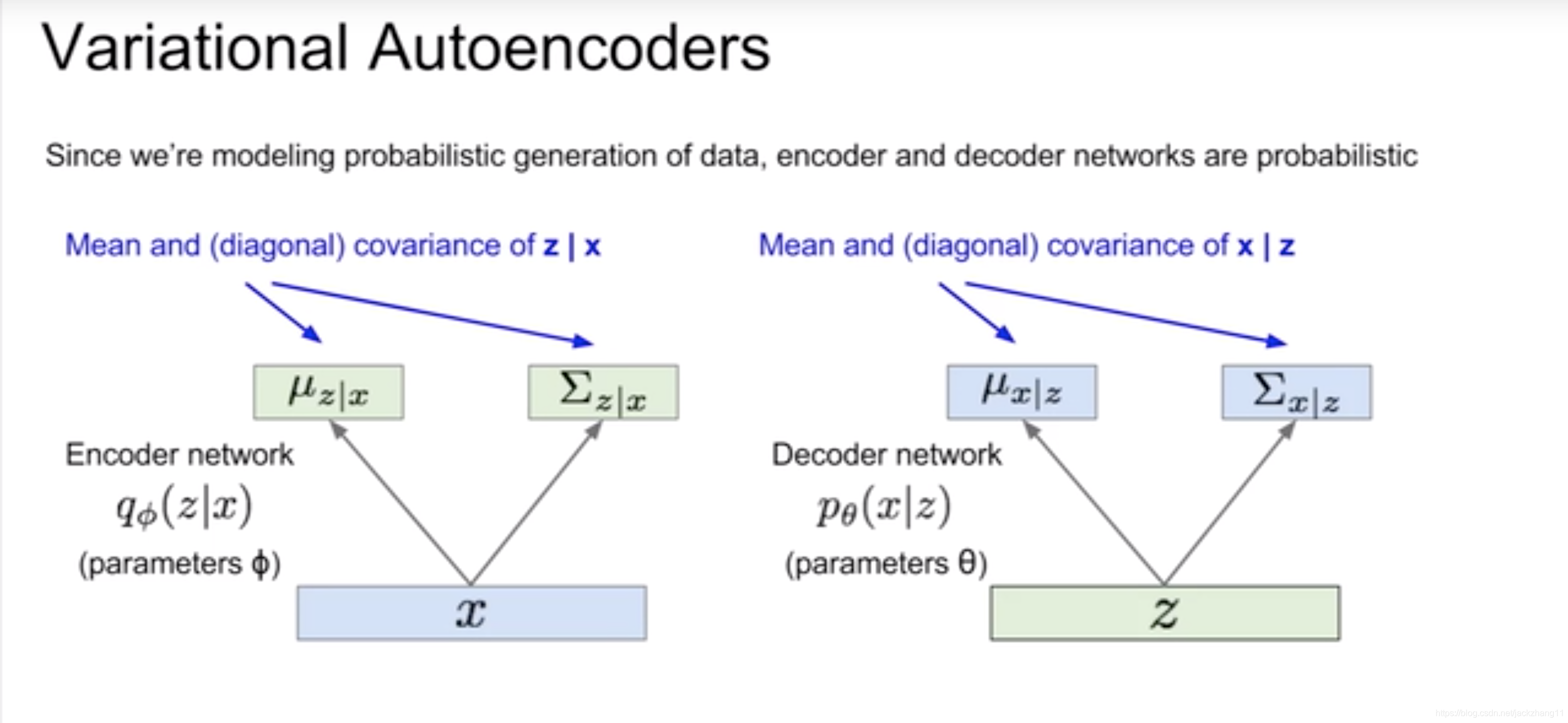
上图中第一个神经网络是编码器encoder，之前我们设定$z$服从简单的正态分布，因此encoder是去求解参数$\varphi$，即均值和方差，从而得到$q(z|x)$。

第二个网络是解码器decoder，解码过程等价于求解$p(x|z)$。

其中，引入编码器encoder的目的，是为了方便求出解码器decoder，下面继续从理论的角度加以证明。

我们重新回到目标式 (1)中的似然，在引入了编码器网络$q(z|x)$以后，就可以进行后续的代数变换了。首先我们的目标是最大化对数似然：

$$maxL=maxlog{p}_{\theta }(x)$$

同时：

$$log{p}_{\theta }(x)={\int }_z{q}_{\varphi }(z|x)log{p}_{\theta }(x)dz$$

$$={\int }_z{q}_{\varphi }(z|x)log(\underset{p_{\theta }(z|x)}{}$$