C允许函数调用它自己,这种调用过程称为递归(recursion)。递归有时难以捉摸,有时却很方便实用。结束递归是使用递归的难点,因为如果递 归代码中没有终止递归的条件测试部分,一个调用自己的函数会无限递归。
递归的原理:其实就是一个栈(stack), 比如求5的阶乘,要知道5的阶乘,就要知道4的阶乘,4又要是到3的,以此类推,所以递归式就先把5的阶乘表示入栈, 在把4的入栈,直到最后一个,之后再从1开始出栈。
先看一个递归调用的例子:
下面是它的函数表述,显然f(x)就调用了自己f(x-1),此为递归。

即f(4)=4*f(3)=4*(3*f(2))=4*(3*(2*f(1))=4*(3*(2*(1*f(0))= 4*3*2*1*1 ←4级递归
![]() 栈:先进后出FILO(first-in last-out)
栈:先进后出FILO(first-in last-out)
#include<stdio.h>
int factorial(int);
int main() {
int n = 4;
printf("%d", factorial(n));
}
int factorial(int n) {
if (n == 0) // 其实这里n==1时return 1更好,因为减少一层递归
return 1;
else
return n * factorial(n - 1);
}#include <stdio.h>
void up_and_down(int);
int main(void) {
up_and_down(1);
return 0;
}
void up_and_down(int n) {
printf("Level %d: n location %p\n", n, &n);
if (n < 4)
up_and_down(n + 1);
printf("LEVEL %d: n location %p\n", n, &n);
}Level 1: n location 0x0012ff48
Level 2: n location 0x0012ff3c
Level 3: n location 0x0012ff30
Level 4: n location 0x0012ff24
LEVEL 4: n location 0x0012ff24
LEVEL 3: n location 0x0012ff30
LEVEL 2: n location 0x0012ff3c
LEVEL 1: n location 0x0012ff48程序代码中的 main() 函数调用up_and_down()函数,这次调用称为“第1级递归”。然后up_and_down()调用自己,这次调用称为“第2级递归”。接着第2级递归调用第3级递归,以此类推。该程序示例共有4级递归。
我们看到,在同一“级”,n有着相同的内存地址,这也揭示了递归逻辑。
我们用图来更直观地表示程序运行的逻辑:
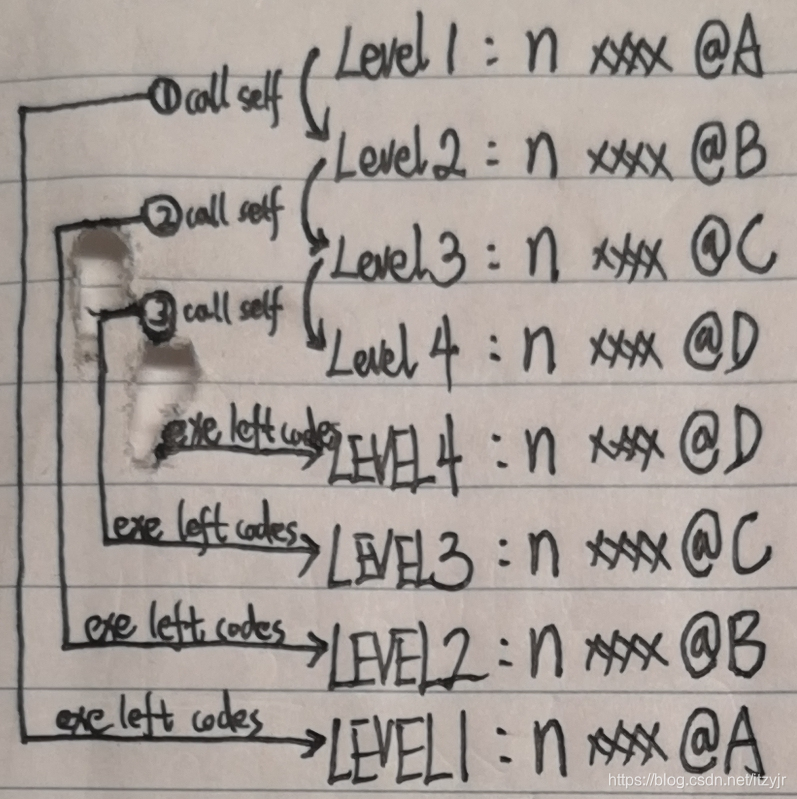
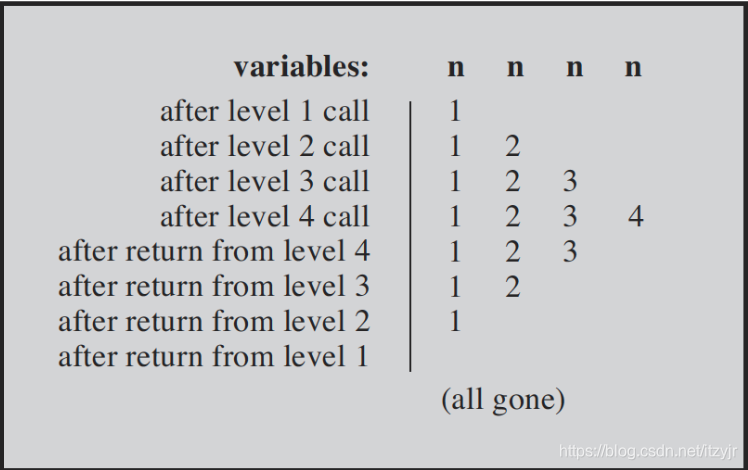
由于是每次调用自己,就导致第二条printf语句在前3级始终没法执行,直到n<4这个结束判断为true,这时的第4级执行完了,第二条printf也就执行了,这时由于第4级结束了,第3级当然就继续执行后面的打印语句了,同样的第3级执行完,就接着执行第2级剩余的语句,然后第2级,最后第1级,程序全部结束。
通过变量n的地址,我们也可以清晰的知道,同一级的n是没变的,说明靠前级是等待后面级执行完毕后再接着执行自己。只是由于递归,导致靠前级无法直接执行完剩余的语句,递归调用自己函数本身就让程序又回到了函数的第一条语句。但最后一级的语句执行完后,靠前一级的就继续接着执行剩余的语句了,这样一级级执行下去直至程序结束。
来看一个解决实际问题的例子:
功能:将一个整数转换成二进制表示法。
算法分析:
二进制是以2为基底的,如二进制101的十进制值= 。由于都是1或0*2^N,而(a+b+c+...)%2,如果a b c ...都能整除2那就得0。对于二进制表示法,可知,末尾前面位一定是0或1*2^N,都可以整除2,所以对2取模结果就一定是最低位的值了(0或1)。同理要得到前两位的值,那就对2^2取模,因为高位一定能整除它,低位一定小于它,取模就是余数,也就是低位本身了。
这里先说明一下取模“%”的规律:比如m%n(m>0,n>0),即m对n整除N次(右移动N次)后的余数:如果m>=n,0=<结果<n;如果m<n,结果=m。余数当然是一定小于除数的。
比如9=“1001”=1*2^3+0*2^2+0*2^1+1*2^0,“1001”%2=1,“1001”/2=1*2^2+0*2^1+0*2^0=“100”,即右移了一位,接着“100”%2=0,“10”%2=0,“1”%2=1,1<2结束递归。组合起来就是二进制的表示“1001”。用一个>=2的整数对2取模,得到的一定是0或1,而这个数一定是二进制表示里面的最低位。通过除以2,再如此这般操作得到最低位的上一位,依次下去。对于8进制、16进制等都可以用此方法完成从10进制到对应进制的转换,只需将%2和/2换成%8和/8或%16和/16等。
#include <stdio.h>
void to_binary(unsigned long n);
int main(void) {
unsigned long number;
printf("Enter an integer (q to quit):\n");
while (scanf("%lu", &number) == 1) {
printf("Binary equivalent: ");
to_binary(number);
putchar('\n');
printf("Enter an integer (q to quit):\n");
}
printf("Done.\n");
return 0;
}
void to_binary(unsigned long n) { /* recursive function */
int r;
r = n % 2;
if (n >= 2)
to_binary(n / 2);
putchar(r == 0 ? '0' : '1');
return;
}Enter an integer (q to quit):
|9
Binary equivalent: 1001
Enter an integer (q to quit):
|255
Binary equivalent: 11111111
Enter an integer (q to quit):
|1024
Binary equivalent: 10000000000
Enter an integer (q to quit):
|q
done.由于m%n是m对n整除N次(右移N次)后的余数,所以比如6%2就一定是十进制6的二进制表示法的最低位,(6/2)%2就是次低位了。
输入6的代码执行流程: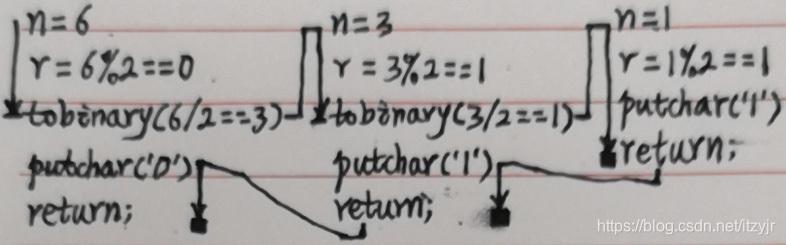 (6÷2=3......0,3÷2=1......1,1<2)
(6÷2=3......0,3÷2=1......1,1<2)
对于其他进制如16进制,输入18代码执行流程: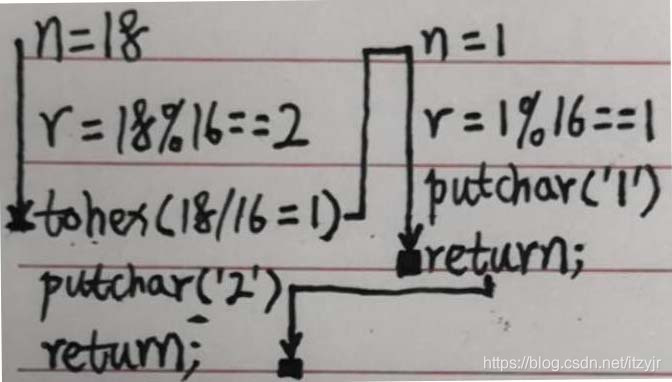 (18÷16=1......2,2<16)
(18÷16=1......2,2<16)
这里附上用位操作,更容易完成同样功能的主要代码:
int main(void) {
char bin_str[CHAR_BIT * sizeof(int) + 1];
int number;
puts("Enter integers and see them in binary.");
while (scanf("%d", &number) == 1) {
itobs(number, bin_str);
...
}
}
char* itobs(int n, char *ps) {
int i;
const static int size = CHAR_BIT * sizeof(int);
for (i = size - 1; i >= 0; i--, n >>= 1)
ps[i] = (01 & n) + '0';
ps[size] = '\0';
return ps;
}函数itobs()中主要涉及位操作符&和>>。对01 & n求值。 01是一个八进制形式的掩码, 该掩码除0号位是1之外, 其他所有位都为0。 因此, 01 & n就是n最后一位的值。 该值为0或1。 但是对数组而言, 需要的是字符'0'或字符'1'。该值(0~9)加上'0'即可完成这种转换(参考:关于ASCII码与转义字符)。 其结果存放在数组中倒数第2个元素中(最后一个元素用来存放空字符)。
递归都可以转化为循环语句,下面是用循环语句完成的十进制转十六进制示例:
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#define MAX 128
int main(void) {
int n = 123;
char arr[MAX + 1] = { 0 };
arr[0] = n % 16;
int m = n / 16;
int m1 = m;
int i = 1;
while (m >= 16) {
arr[i++] = m % 16;
m1 = m;
m /= 16;
}
arr[i] = m1;
for (; i >= 0; i--) {
printf("%x", arr[i]);
}
puts("\n——————");
printf("%d,%d\n", (sizeof arr) / sizeof(char), strlen(arr));
return 0;
}7b
——————
129,2sizeof计算的是数组大小,即MAX+1=129;strlen是计算从头开始到'\0'结束但不包含'\0'的字符数量,所以此处为2。
调试查看数组arr的存储值:
如果n=0,则: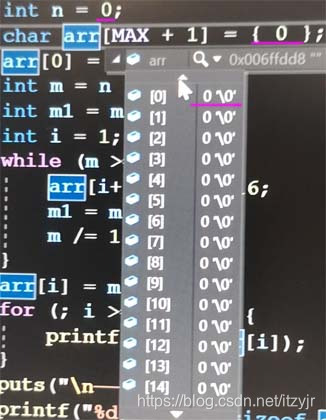 所以strlen(arr)==0而不是1。
所以strlen(arr)==0而不是1。
如果n=123,但不初始化arr={0},则: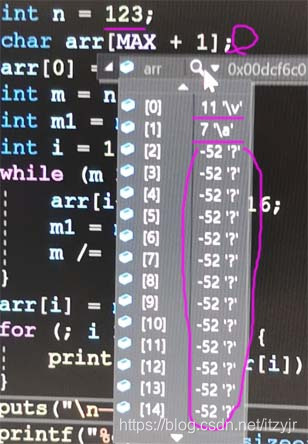 此时输出strlen==141>sizeof???。注意到[0]==11 '\v',[1]==7 '\a',[2]~[128]=-52 '?'(随机乱码),[]=并排的前者是整数后者是它的转义字符,如下图:
此时输出strlen==141>sizeof???。注意到[0]==11 '\v',[1]==7 '\a',[2]~[128]=-52 '?'(随机乱码),[]=并排的前者是整数后者是它的转义字符,如下图:
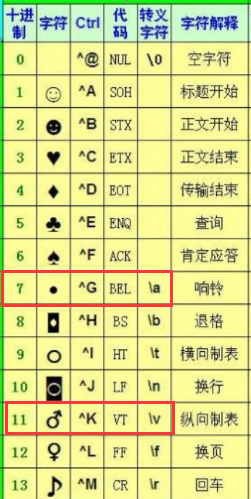
再来看一个完成斐波纳契数列(Fibonacci Numbers)的例子:
斐波纳契数列第一个数是1,第二个数也是1,后面的数都是前两个数的和,即:1,1,2,3,5,8,13,...。现定义一个函数Fibonacci(n),如果n=1或n=2,返回1,否则返回Fibonacci(n-1)+Fibonacci(n-2)。
unsigned long Fibonacci(unsigned n) {
if (n > 2)
return Fibonacci(n-1) + Fibonacci(n-2);
else
return 1;
}最后看一个经典的汉诺塔实例:
什么是汉诺塔?
有三根杆子A,B,C。A杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆:
1.每次只能移动一个圆盘;
2.大盘不能叠在小盘上面。

#include<stdio.h>
void hannuo(int n, char a, char b, char c);
void move(char x, char y);
int main() {
int n;
printf("请输入要移动的块数:");
scanf("%d", &n);
hannuo(n, 'a', 'b', 'c');
return 0;
}
void hannuo(int n, char a, char b, char c) {
if (n == 1)
move(a, c); // 当n只有1个的时候直接从a移动到c
else {
hannuo(n - 1, a, c, b); // 把a的n-1个盘子通过c移动到b
move(a, c); // 把a的最后1个盘(最大的盘)移动到c
hannuo(n - 1, b, a, c); // 把b上面的n-1个盘通过a移动到c
}
}
void move(char x, char y) {
printf("%c->%c\n", x, y);
}请输入要移动的块数:|3
a->c
a->b
c->b
a->c
b->a
b->c
a->c算法分析:
步骤1:如果是一个盘子,直接将a柱子上的盘子从a移动到c。
否则:
步骤2:先将a柱子上的n-1个盘子借助c移动到b(图1),没有c柱子肯定是不能移动的。已知函数原型是hannuo(int n,char a,char b,char c):代表将a柱子上的盘子借助b柱子移动到c柱子。这里调用函数的时候是将a柱子上的n-1个盘子借助c柱子移动到b柱子,所以这里需要将位置调换一下hannuo(n-1,a,c,b)。
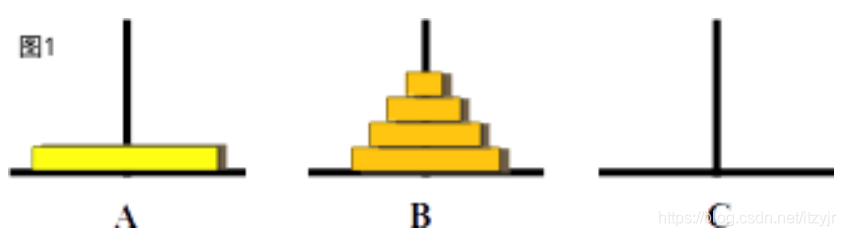
步骤3:此时移动完如(图1),但是还没有移动结束,这时要将a柱子上的最后一个(第n个)盘子直接移动到c(图2)。
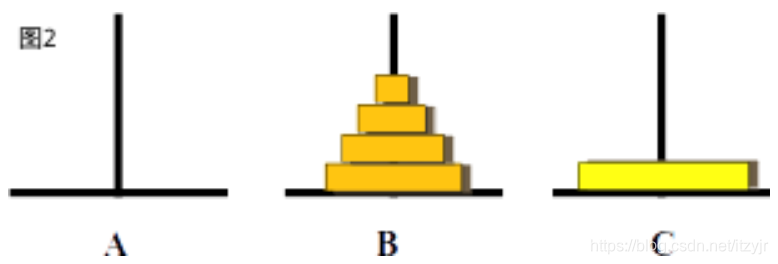
步骤4:最后将b柱子上的n-1个盘子借助a移动到c(图3)。

这样递归算法就完成了。如果第一遍没懂,仔细读三四遍应该就没问题了。





 本文深入解析递归原理,包括栈机制与终止条件,并通过阶乘、二进制转换、斐波纳契数列及汉诺塔问题的实例,展示递归在解决复杂问题中的运用。
本文深入解析递归原理,包括栈机制与终止条件,并通过阶乘、二进制转换、斐波纳契数列及汉诺塔问题的实例,展示递归在解决复杂问题中的运用。

















 6015
6015

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










