OpenCV主成分分析(PCA)简介

最新推荐文章于 2024-03-06 16:58:32 发布
最新推荐文章于 2024-03-06 16:58:32 发布
阅读量724 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： OpenCV完整教程 C和C++Everything教程
不予转载，严禁转载，违者必纠。
本文链接：https://blog.youkuaiyun.com/it_xiangqiang/article/details/115956486
本文介绍了如何使用OpenCV库进行主成分分析(PCA)，包括PCA的目标、计算过程和源代码解释。PCA是一种统计方法，用于降维和提取数据集的主要特征。文中详细展示了如何计算特征向量和特征值，并通过实例解释PCA在图像处理中的应用，如提取图像对象的方向并进行可视化。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

OpenCV主成分分析PCA

主成分分析(PCA)

目标

在本教程中，您将学习如何：
使用OpenCV类cv :: PCA计算对象的方向。

什么是PCA？

主成分分析（PCA）是一种统计过程，可提取数据集的最重要特征。
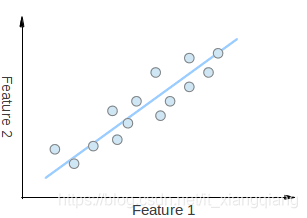
在这里插入图片描述
如上图所示，请考虑您拥有一组2D点。每个维度都对应于您感兴趣的特征。这里有些人可能会说这些点是按随机顺序设置的。但是，如果外观更好，您会发现存在难以消除的线性图案（由蓝线表示）。PCA的关键是降维。降维是减少给定数据集的维数的过程。例如，在上述情况下，可以将一组点近似为一条直线，因此可以将给定点的维数从2D减少到1D。

此外，您还可以看到，这些点沿蓝线的变化最大，远比沿特征1或特征2的变化大。这意味着，如果您知道一个点沿蓝线的位置，则与该点有关的信息要比仅知道该点在特征1轴或特征2轴上的位置要多。

因此，PCA使我们能够找到数据变化最大的方向。实际上，在图中的点集上运行PCA的结果由2个称为特征向量的向量组成，它们是数据集的主要组成部分。
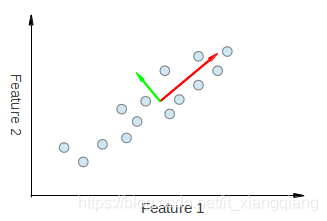
在这里插入图片描述
每个特征向量的大小被编码在相应的特征值中，并指示数

了解本专栏 订阅专栏 解锁全文 超级会员免费看
OpenCV主成分分析（PCA）及保留差异量的实例编程
CyberByte的博客
09-08 129
在本文中，我们将介绍如何使用OpenCV库进行PCA分析，并演示如何指定保留的差异量。在本文中，我们将介绍如何使用OpenCV库进行PCA分析，并演示如何指定保留的差异量。接下来，我们根据指定的保留差异量计算要保留的特征向量数目。然后，我们将数据转换到新的特征空间。为了进行PCA分析，我们需要将数据标准化，即使每个特征的均值为0，方差为1。为了进行PCA分析，我们需要将数据标准化，即使每个特征的均值为0，方差为1。然后，我们指定要保留的差异量为0OpenCV主成分分析（PCA）及保留差异量的实例编程。
OpenCV主成分分析详解及编程示例
PixelInk的博客
09-06 201
PCA的目标是通过线性变换将原始数据投影到一个新的坐标系中，使得投影后的数据具有最大的方差。通过保留较高方差的主成分，我们可以实现数据的降维，同时保留尽可能多的信息。在本文中，我们将详细介绍OpenCV中的主成分分析算法，并提供相应的编程示例。通过选择不同的主成分数量，我们可以实现数据的降维，并根据需要保留适当的信息量。请注意，PCA还可以应用于图像处理等更复杂的情况，但本文仅涵盖了基本的概念和示例。在上述代码中，我们使用了前两个主成分的主成分向量和特征值，通过矩阵乘法和加法操作来重构原始数据。
基于OpenCV的图像主成分分析
09-12
使用PCA，对单图像提取主成分分析，达到图像降维的目的，可以学习如何使用OpenCV实现PCA技术。
OpenCV统计应用-PCA主成分分析(图像完全解读)
王伟挺的专栏
05-09 7844
在图形识别方面,主成分分析(Principal Comonents Analysis,PCA)算是比较快速而且又准确的方式之一,它可以对抗图形平移旋转的事件发生,并且藉由主要特征(主成分)投影过后的数据做数据的比对,在多个特征信息里面,取最主要的K个,做为它的特征依据,在这边拿前面共变量矩阵的数据来做沿用,主成分分析使用的方法为计算共变量矩阵,在加上计算共变量矩阵的特征值及特征向量,将特征值以及所
OpenCV实现主成分分析（PCA）
Joemt
11-09 3868
这几天将大学期间做的项目，尝试将MATLAB代码转为C++。 这里对主成分做一个备忘。 这里先简单说一下我对主成分的理解，就是将数据降维。一组数据间的各个元素可能存在一定的关联。比如：一组数据[1 2 3]，那么3可以由1+2表示，那么就可以用[1 2]来表示[1 2 3]这组数据，这样在实际数据处理时，就可以只用处理2维的数据，不用处理3维数据，可以提高程序效率。详细的原理讲解，网上大神们讲得
主成分分析（PCA）简介 OpenCV-Python v4.7.0
hirshdz327的博客
09-26 335
在这里，有些人可能会认为这些点的顺序是随机的。首先，需要将数据排列在一个大小为 n x 2 的矩阵中，其中 n 是我们拥有的数据点的数量。这意味着，与只知道点在特征 1 轴或特征 2 轴上的位置相比，如果知道点在蓝线上的位置，就能获得更多关于点的信息。事实上，在图中的点集合上运行 PCA 的结果由 2 个称为特征向量的向量组成，它们是数据集的主成分。代码会打开一幅图像，找出检测到的感兴趣物体的方向，然后通过绘制检测到的感兴趣物体的轮廓线、中心点以及关于提取方向的 x 轴和 y 轴，将结果可视化。
opencv——PCA（主要成分分析）数学原理推导
明月清风@的博客
05-28 1182
引言： 最近一直在学习主成分分析(PCA)，所以想把最近学的一点知识整理一下，如果有不对的还请大家帮忙指正，共同学习。 首先我们知道当数据维度太大时，我们通常需要进行降维处理，降维处理的方式有很多种，PCA主成分分析法是一种常用的一种降维手段，它主要是基于方差来提取最有价值的信息，虽然降维之后我们并不知道每一维度的数据代表什么意义，但是它将主要的信息成分保留了下来，那么PCA是如何实现的呢？ 本......
OpenCV主成分分析（PCA）方法用于计算轮廓的角度
WzisTypescript的博客
09-17 339
在计算机视觉领域中，主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维技术，它可以在高维数据中找到最重要的特征。在OpenCV中，PCA也可以应用于计算轮廓的角度，这对于形状分析和物体识别非常有用。本文将详细介绍如何使用OpenCV的PCA方法来计算轮廓的角度，并提供相应的源代码。然后，我们将轮廓坐标点作为数据集，使用PCA分析找到主成分的特征向量，并计算角度。使用PCA的主要思想是将轮廓坐标点作为数据集，然后通过PCA分析找到主成分（主轴），进而计算角度。
使用OpenCV进行主成分分析（PCA）以提取对象方向的示例（C++）
带你成为别人眼中的大佬！
09-05 307
主成分分析（Principal Component Analysis，PCA）是一种常用的统计方法，用于将高维数据降低到较低维度的表示，同时保留尽可能多的信息。主成分分析（Principal Component Analysis，PCA）是一种常用的统计方法，用于将高维数据降低到较低维度的表示，同时保留尽可能多的信息。接下来，我们使用PCA类执行主成分分析，并可视化主成分向量和平均图像使用OpenCV进行主成分分析（PCA）提取对象方向的实例（C++）在进行PCA之前，我们需要将图像转换为一维的数据表示。
【OpenCV 例程 300篇】236. 特征提取之主成分分析（OpenCV）
youcans的博客
07-22 2662
主成分分析（Principal Components Analysis，PCA）是一种基于统计的数据降维方法，又称主元素分析、主分量分析。 在 Python 语言中，OpenCV 提供了 PCA 类的接口函数 **cv.PCACompute()**，**cv.PCAProject()** 和 **cv.PCABackProject()**。......
(八)OpenCV人脸识别_03_PCA主成分分析
01-20
PCA原理:(一个分析多维分布并且从中提取出带有最多信息量的维度子集的方法)(无监督:基于方差提取最有价值的信息) 通过对高维数据分析发现他们的相同与不同表达为一个低维数据模式 主成分不变、细微损失、高维数据到低维数据 PCA:样本数据、减去均值、计算协方差矩阵(标准差、方差越大,离散程度越大)、计算特征值与特征向量、根据特征值排序保留前K个主成分特征向量、形成新的数据样本。 输出数据 = 前K个特征向量组合 x 均值调整之后的数据 #include #include using namespace std; using namespace cv; double calcPCA(vector
OPENCV中的PCA使用
landsuper的专栏
07-26 5242
对于PCA，一直都是有个概念，没有实际使用过，今天终于实际使用了一把，发现PCA还是挺神奇的。 在OPENCV中使用PCA非常简单，只要几条语句就可以了。1、初始化数据 //每一行表示一个样本 CvMat* pData = cvCreateMat( 总的样本数, 每个样本的维数, CV_32FC1 ); CvMat* pMean = cvCreateMat(1, 样本的维数, CV_32FC1); //pEigVals中的每个数表示一个特征值 CvMat* pEigVals = cvCreateMat(1,
OpenCV8：主成分分析
smart boy
06-09 325
主成分分析（principle components analysis, PCA） 如果成分太多，可以使用pca识别数据中的重要部分，并将其按照重要程度排序。当需要处理很大维度的特征值时，利用PCA降维，可以在不损失重要特征的同时，降低其处理复杂度。 代码 import os import sys import platform import numpy as np import...
OpenCV3.3中主成分分析(Principal Components Analysis, PCA)接口简介及使用
网络资源是无限的
01-13 3969
OpenCV3.3中主成分分析(Principal Components Analysis, PCA)接口简介及使用
opencv pca主成分分析
nanguazhuo的专栏
12-08 522
关于主成分分析，这玩意在数据分析领域就跟1+1=2一样，实在是太基础了，于是就不解释了。 cv::Mat dataWrap(rows,2,CV_64FC1, (cv::Point2d *)(varInputData.first)); cv::PCA varPCA(dataWrap,{ /*mean*/ }, cv::PCA::DATA_AS_RO
opencv mat初始化_14、OpenCV主成分分析、奇异值分解和随机数生成
weixin_39941262的博客
11-26 275
最近太忙了，今天抽空更新一篇。随着OpenCV库的发展，引入新封装的对象变得越来越普遍，这些封装功能过于复杂，无法与单个功能相关联，并且如果作为一组功能实施，会导致库的整体功能空间变得太混乱。因此，新功能通常由相关的新对象类型来表示，它可以执行任何功能。大多数这些都有一个重载的operator()。他们可以设置需要的任何数据或配置，并且他们被要求通过普通成员函数来执行，或者通过重载operator...
OpenCV与机器学习：OpenCV实现主成分分析
最新发布
艾醒的博客
03-06 1368
维数灾难是指出现一定数量的特征（或者维度）后，分类器的性能将开始下降。特征越多，数据集中的信息就越多。但是，如果考虑的特征超过了所需的特征，分类器甚至会考虑异常值或者会过拟合数据集。因此分类器的性能开始下降，而不是上升。降维技术允许我们在不丢失太多信息的情况下，找到高维数据的一种紧凑表示。
OpenCV PCA介绍
泠山的博客
08-23 2427
主成分分析(PCA)是一个统计过程，提取一个数据集最重要的特征。假设有一组2D点，如上图所示。每个维度对应一个感兴趣的特征。有些人可能会说，这些点的设置顺序是随机的。然而，如果仔细观察，会发现这里有一个很难忽略的线性模式(由蓝色线表示)。主成分分析的一个关键点是降维。降维是减少给定数据集的维数的过程。例如，在上述情况下，可以将一组点近似为一条直线，从而将给定点的维数从2D降至1D。此外还可以看到，这些点沿着蓝线变化最大，比沿着特征1或特征2轴变化更大。
【OpenCV 例程 300篇】235. 特征提取之主成分分析（sklearn）
youcans的博客
07-20 2409
主成分分析（Principal Components Analysis，PCA）是一种基于统计的数据降维方法，又称主元素分析、主分量分析。 SKlearn 工具包提供了多种降维分析方法。sklearn.decomposition.PCA 类是 PCA算法的具体实现。 **sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)** SKlearn 工具包针对实际问题的特殊性，发展了各种改进算法.........
opencv 主成分分析c++
12-28
以下是使用OpenCV实现主成分分析的C++代码示例： ```cpp #include <opencv2/opencv.hpp> #include <fstream> using namespace cv; using namespace std; // data：输入数据 // path：数据保存路径 Mat My_PCAs(Mat data, String path) { FileStorage f_pca(path, FileStorage::READ); int num; Mat mean, coff; f_pca["num"] >> num; f_pca["mean"] >> mean; f_pca["coff"] >> coff; f_pca.release(); Mat result = (data - mean) * (coff.t()); mean.release(); coff.release(); return result; } ``` 请注意，这只是一个函数的示例，你需要根据你的具体需求进行调整和使用。你需要将输入数据和数据保存路径作为参数传递给`My_PCAs`函数，并且确保你已经正确设置了OpenCV库和文件路径。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

源代码大师

赏点狗粮吧

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值