用Python实现汉诺塔递归解法

最新推荐文章于 2024-09-02 20:25:19 发布

原创最新推荐文章于 2024-09-02 20:25:19 发布 · 681 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#python

Python 专栏收录该内容

3 篇文章

订阅专栏

本文通过Python展示了汉诺塔问题的递归解决方案，仅用5行代码实现。理解递归的关键在于将3个盘子分成两部分，然后通过将盘子视为整体并移动到目标位置来解决问题。当有n个盘子时，需要移动2的n次方减1步。代码来源于《C++编程–数据结构与程序设计方法》，并提供了其他书籍中关于递归思想的推荐。

看谭老师著名的C语言教材一直没有搞懂汉诺塔的递归原理，
偶尔看到一本c++教材上讲解的比较详细，就用python写了一个解法，总共5行代码，还是挺简单的。写的时间比较久远了，等我找到那本书，再把书中的解析附上。

# 参数的含义为（盘子总数，起始杆，中间杆，目标杆）
def moveDisk(count, needle1, needle2, needle3):
	if count > 0:
		# 将除最底盘以外的盘子从1杆移到2杆
		moveDisk(count-1, needle1, needle3, needle2) 
		# 将最底盘从1杆移到3杆
		print("move disk", count, "from", needle1, "to", needle3）
		# 将除最底盘以外的盘子从2杆移到3杆，任务完成
		moveDisk(count-1, needle2, needle1, needle3)

验证一下结果

#当有三个盘子的时候
moveDisk(3, 'needle1', 'needle2', 'needle3')


输出结果：
1. move disk 1 from needle1 to needle3
2. move disk 2 from needle1 to needle2
3. move disk 1 from needle3 to needle2
4. move disk 3 from needle1 to needle3
5. move disk 1 from needle2 to needle1
6. move disk 2 from needle2 to needle3
7. move disk 1 from needle1 to needle3
[Finished in 0.2s]

理解的关键在于，将3个盘子分成两部分，即上面的盘子（2个）和底盘（第3个），将上面的2个盘子视为一个整体，这样，将3个盘子从1杆移到3杆只需三步：

将上面的盘子从1杆移到2杆（前3步）
将底盘从1杆移到3杆（第4步）
将上面的盘子从2杆移到3杆（后3步）

像不像把大象装进冰箱这个梗的步骤，只要按递归思想实现了代码，具体的函数如何调用，就交给计算机吧。

当有n个盘子的话，最少需要移动2的n次方减1步。即，3个盘子需要移动2^3-1

终于找到了，原书是《C++编程–数据结构与程序设计方法》P339：

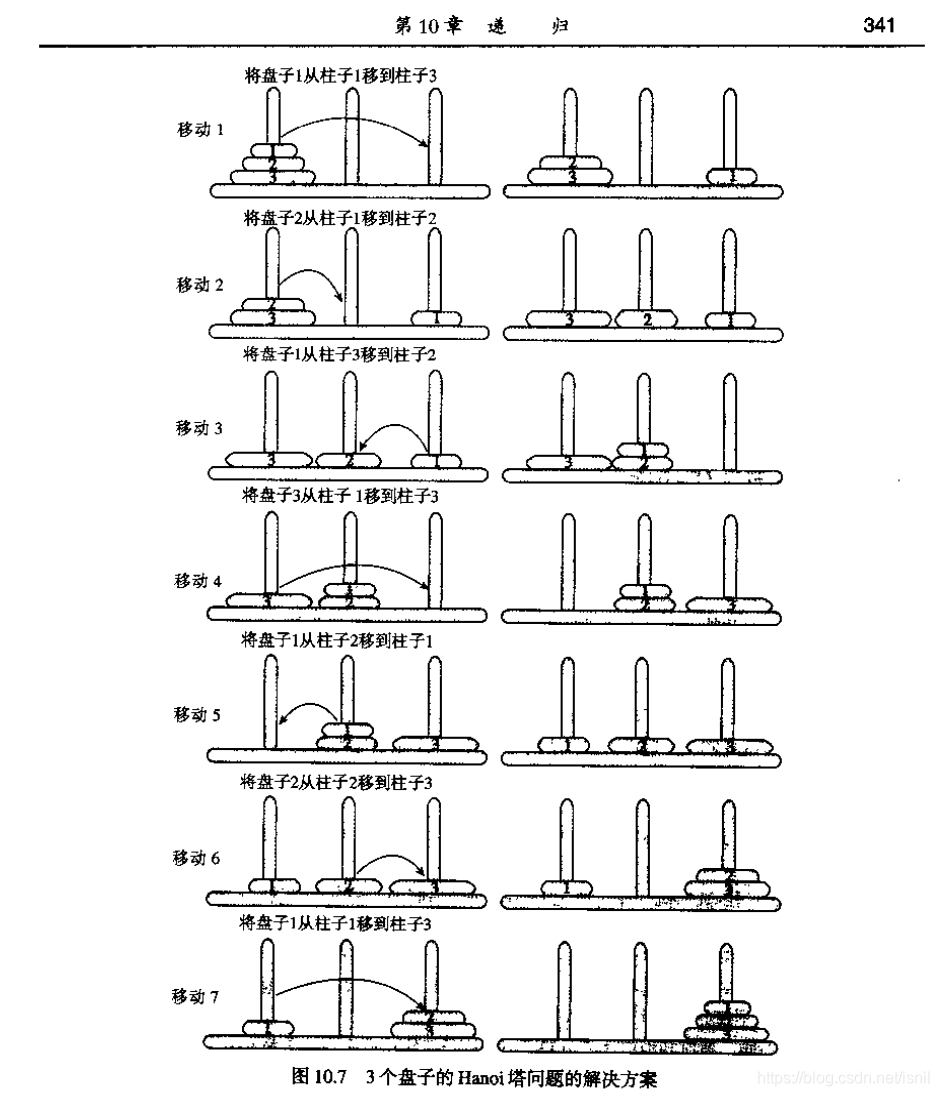
在这里插入图片描述
关于递归思想的理解，可以参考《数据结构与算法分析——C++描述》第三版。
文中c++代码转化为python代码为：

def print_out(n):
	if n >= 10:
		print_out(n // 10)  # 先打印7654 （76543//10）
	print(n % 10)           # 接着打印3 （76543%10）

print_out(76543)

当然，目前看到的对递归最详细易懂的解释是《C语言程序设计与问题求解（第七版）》第九章，这本书英文名为《problem solving and program design in c》，也被翻译为《C语言详解》