哈夫曼树
哈夫曼树的定义
相当于每个结点的概率*树高之和
最优二叉树/哈夫曼树：WPL最小的树
哈夫曼树的构造：权值最小的两棵二叉树合并...*n
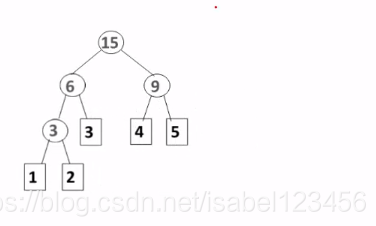
利用堆选取最小的结点
哈夫曼树的特点：
没有度为1的结点
n2 = n0 -1
n个叶子结点的哈夫曼树一共 2n -1 个结点
哈夫曼树任意非叶节点的左右子树交换之后仍为哈夫曼树
对于同一组权值，存在不同结构的哈夫曼树
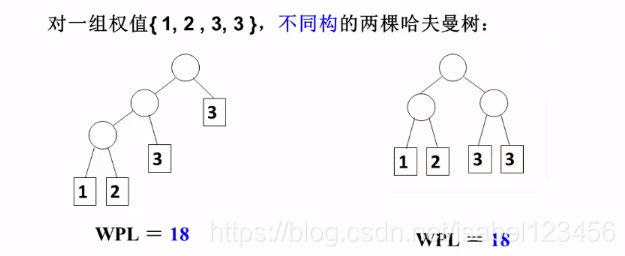
前缀码：任何字符的编码都不是另一字符编码的前缀，可以无二义地编码
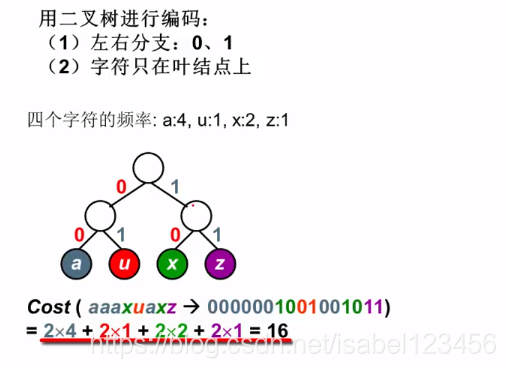
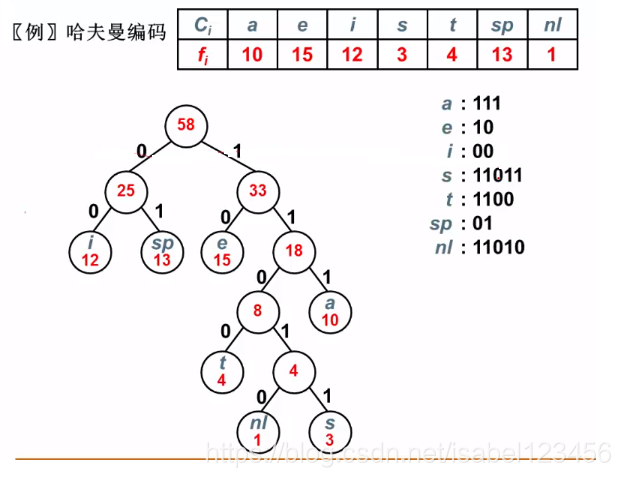
集合的表示
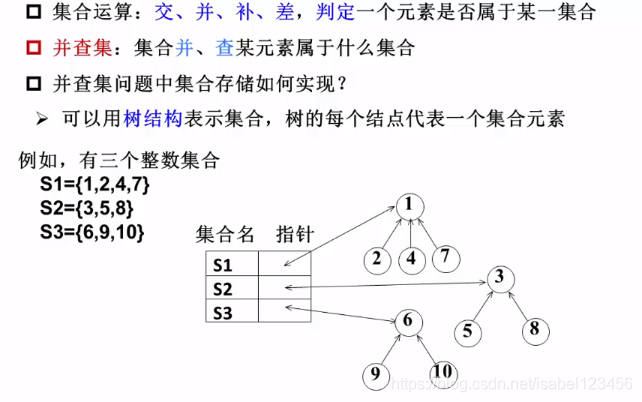
下标 数据 父节点下标
数据结构与算法（五）
本文详细介绍了哈夫曼树的基本概念，包括其定义、特点及构造方法。阐述了哈夫曼树作为最优二叉树的应用场景，以及如何通过堆来选择最小结点进行树的合并。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
