数据结构与算法（四）

数据结构-数组（线性结构）和二叉搜索树（非线性结构）操作

能查找是否具有元素X

能找到最大值和最小值

能插入和删除元素

区别：二叉搜索树的存储结构和数组不一样，二叉搜索树查找效率高于数组

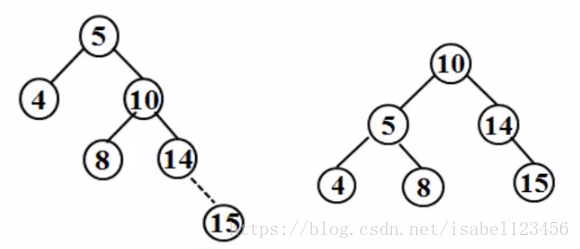
判断以下是否为二叉查找树

 

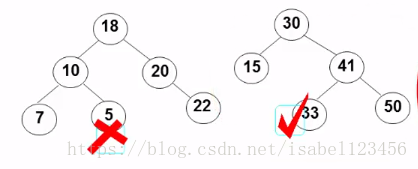
查找某个元素X

二叉搜索树中最大元素一定是在树的最右分枝的端节点上，一定没有右儿子

二叉搜索树中最小元素一定是在树的最左分枝的端节点上，一定没有左儿子

二叉树的删除

1. 叶节点--直接删除 修改其父节点指针为NULL

2. 只有一个孩子结点的结点--删除该结点，其父节点指向要删除结点的孩子结点

3. 有两个孩子结点的结点--删除该结点，要删除结点的位置用左子树中最大的元素或者右子树中最小的元素替代。

     （左最小、右最大的结点只有一个孩子结点）

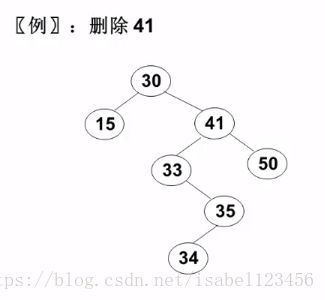
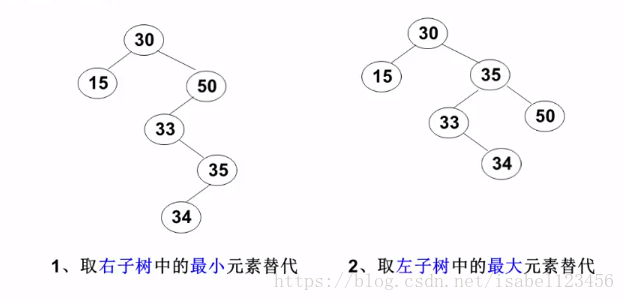
平衡二叉树

 

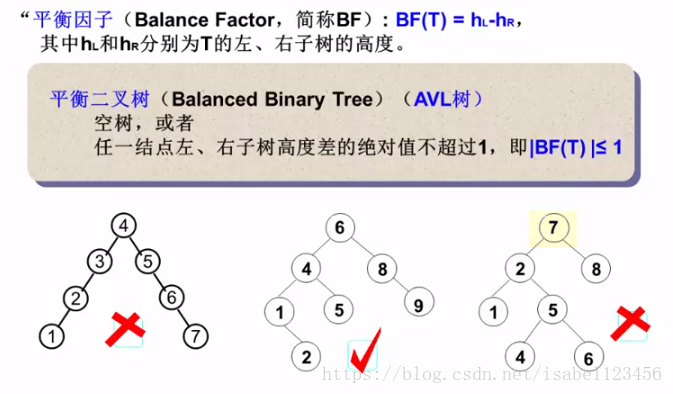
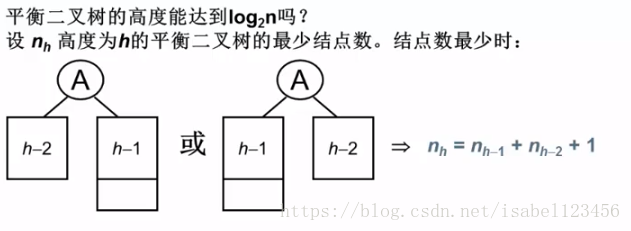
高度 = 深度 - 1

树的高度：从所有叶节点开始数高度到根节点，其中的最大值；也就是从结点x向下到某个叶结点最长简单路径中边的条数。

树的深度：树根下中所有分支结点层数的最大值，递归定义。（一般以根节点深度层数为1）--即层数

平衡二叉树的调整

不平衡的”发现者“，”麻烦结点“（引起不平衡的结点）被发现的位置称其为 RR/LL/LR/RL插入，需要对应的旋转。

RR旋转

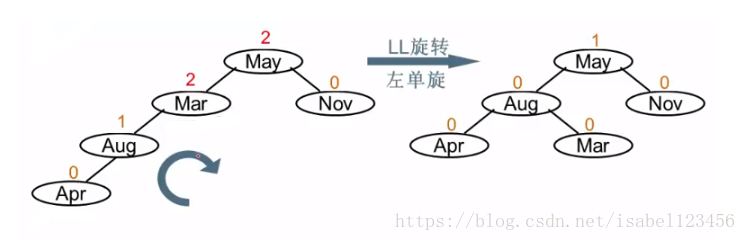
LL旋转 加了Apr

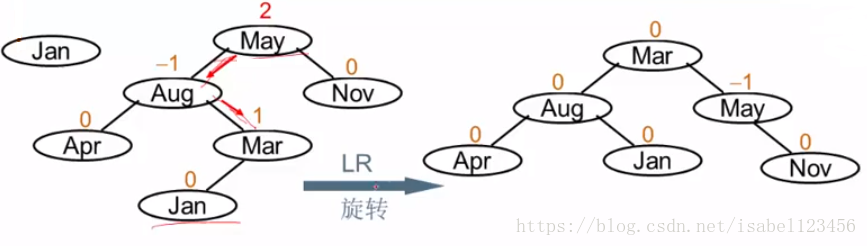
LR旋转 加了Jan 被影响的是May Jan在May的左子树 右分枝...麻烦结点的父结点替换被影响的结点

 

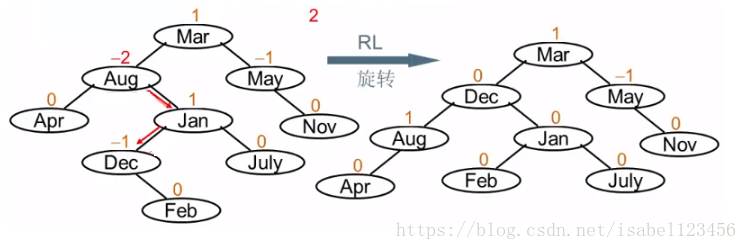
RL旋转 加了Feb 被影响的是Aug Feb在Aug的右子树 左分支..麻烦结点的父结点替换被影响的结点

堆

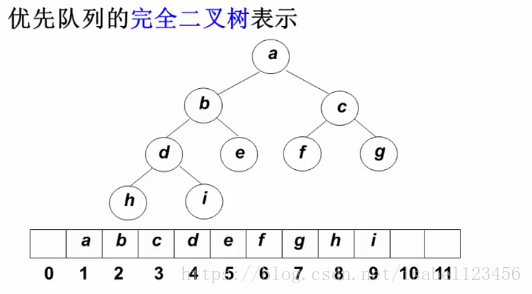
用数组表示的完全二叉树

特点：任意结点的元素值是其子树的最大值/最小值

最大堆，大顶堆：最大值

最小堆，小顶堆：最小值

最大堆的操作有

创建一个最大堆

判断最大堆是否为空

判断最大堆是否为满

插入一个元素

返回最大元素