文章标题:格子玻尔兹曼方法(LBM)模拟压力驱动流的不规则边界处理及压力速度分布的Matlab输出
一、引言
格子玻尔兹曼方法(Lattice Boltzmann Method,简称LBM)是一种用于模拟流体流动的数值方法。它通过模拟粒子在格子上的运动来模拟流体的宏观行为。本文将探讨使用LBM模拟压力驱动流的不规则边界处理,并输出压力速度分布的Matlab实现。
二、格子玻尔兹曼方法(LBM)简介
格子玻尔兹曼方法是一种计算流体动力学方法,其基本思想是将流体看作是由一系列的粒子组成,这些粒子在离散的格子上进行碰撞和迁移。LBM可以有效地模拟各种复杂的流体流动现象,包括压力驱动流。
三、压力驱动流模拟
在压力驱动流中,流体的运动主要由压力梯度引起。我们可以通过设定进出口的压力差来模拟这种流动。在LBM中,我们可以通过调整格子上的粒子分布来模拟这种压力驱动的流动。
四、不规则边界处理
在模拟过程中,我们常常需要处理不规则边界。这可以通过使用适当的边界条件来实现。常见的边界条件包括反弹边界条件和外部力边界条件等。对于不规则边界,我们可以采用拟合方法或离散化方法将边界近似为规则的形状,或者采用更复杂的边界处理方法如动态边界处理方法等。
五、Matlab实现
在Matlab中,我们可以使用自定义的LBM算法来模拟压力驱动流。首先,我们需要定义格子、粒子的初始分布以及边界条件。然后,我们可以使用LBM算法进行迭代计算,得到流体的速度和压力分布。最后,我们可以使用Matlab的图形绘制功能来输出压力速度分布。
六、结论
通过使用LBM和Matlab,我们可以有效地模拟压力驱动流的不规则边界处理及压力速度分布。这种方法可以用于研究各种复杂的流体流动现象,如多孔介质中的流体流动、微流控等。同时,这种方法也可以用于优化流体设备的设计,提高设备的性能和效率。
七、未来展望
未来,我们可以进一步研究LBM在更复杂的流体流动现象中的应用,如湍流、多相流等。此外,我们还可以研究更高效的LBM算法和更精确的边界处理方法,以提高模拟的精度和效率。同时,我们也可以将LBM与其他数值方法相结合,如有限元方法、有限差分方法等,以实现更全面的流体流动模拟。
格子玻尔兹曼方法lbm模拟压力驱动流(不规则边界)并输出压力速度分布 matlab
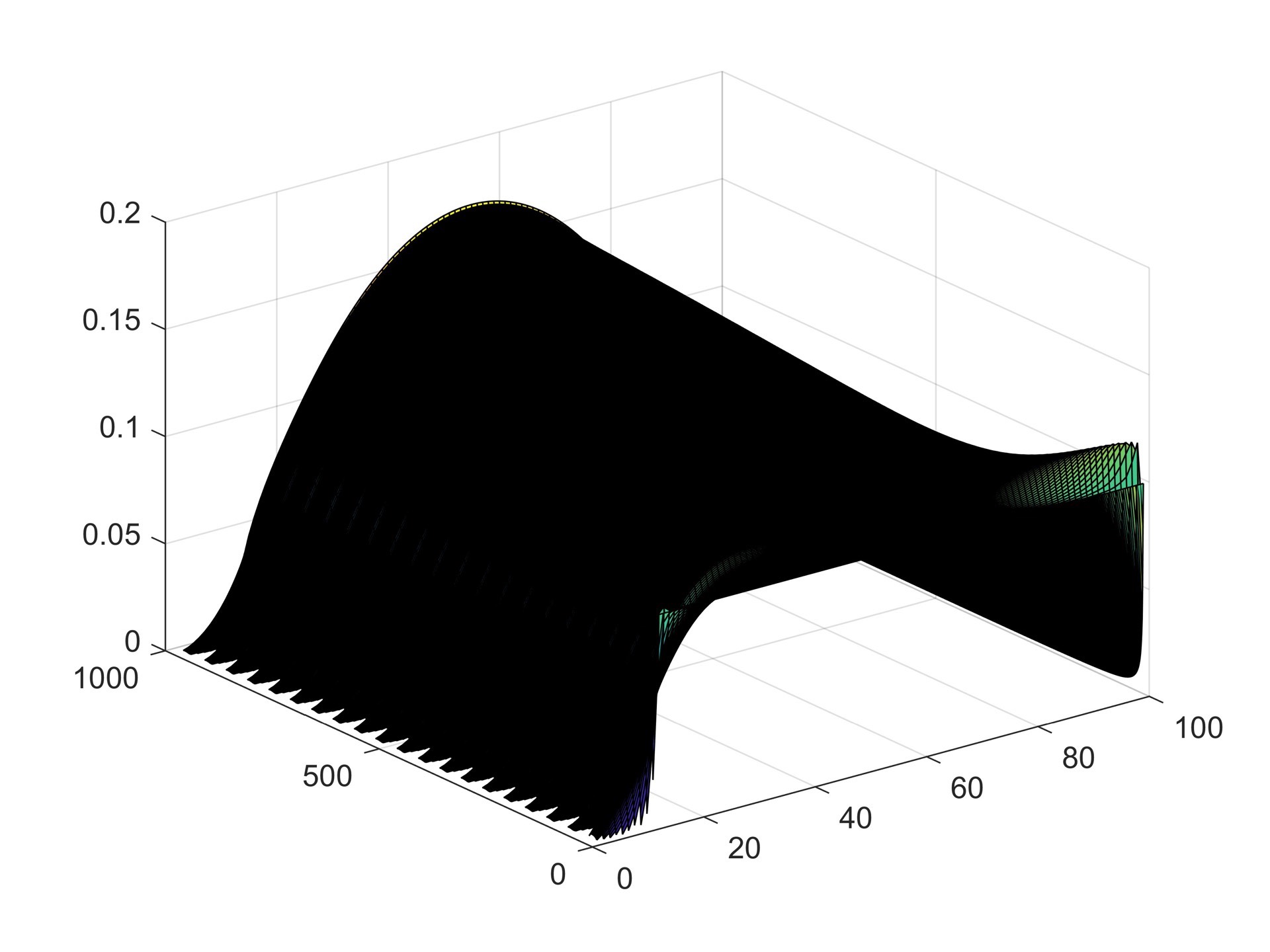
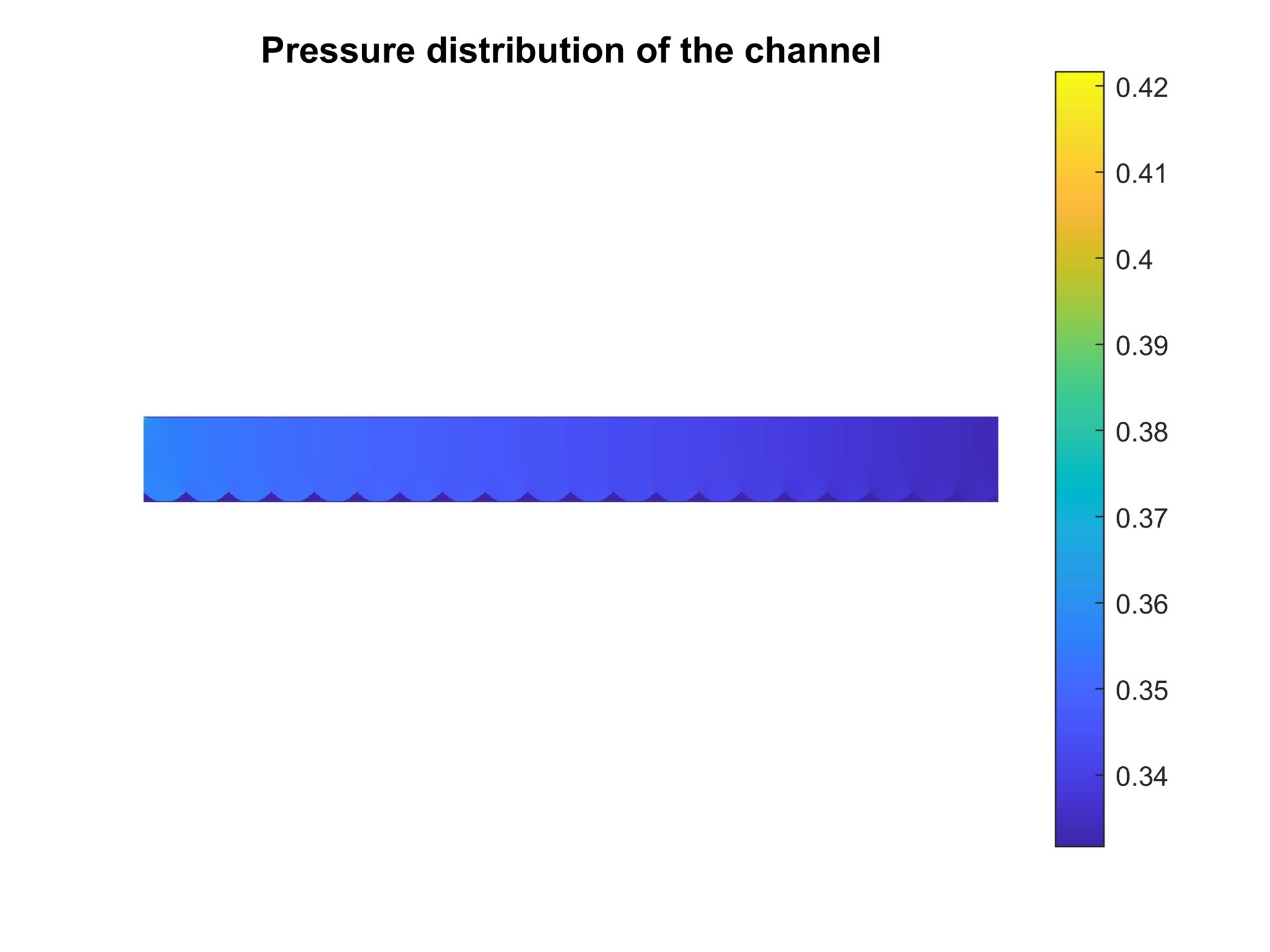
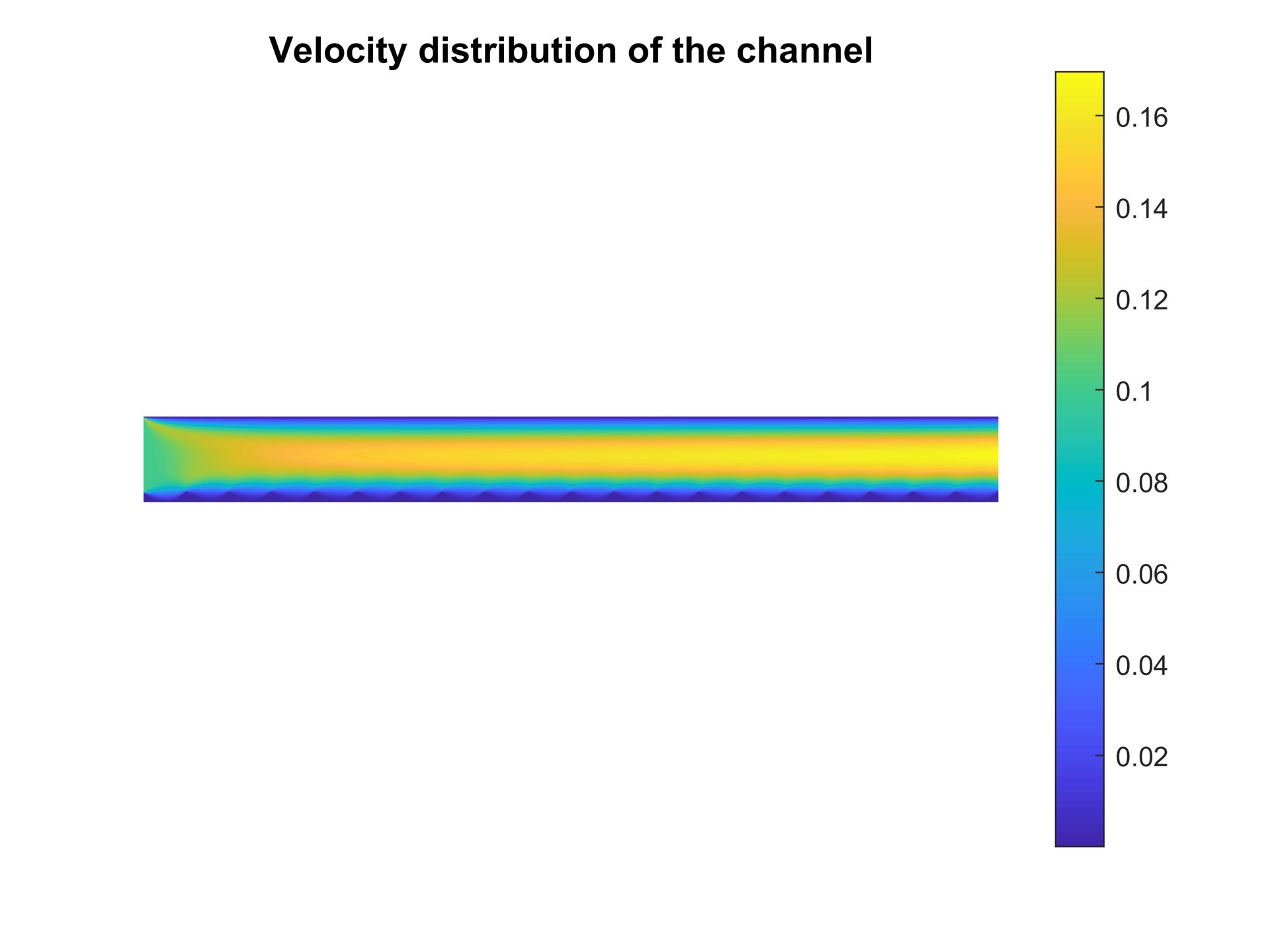
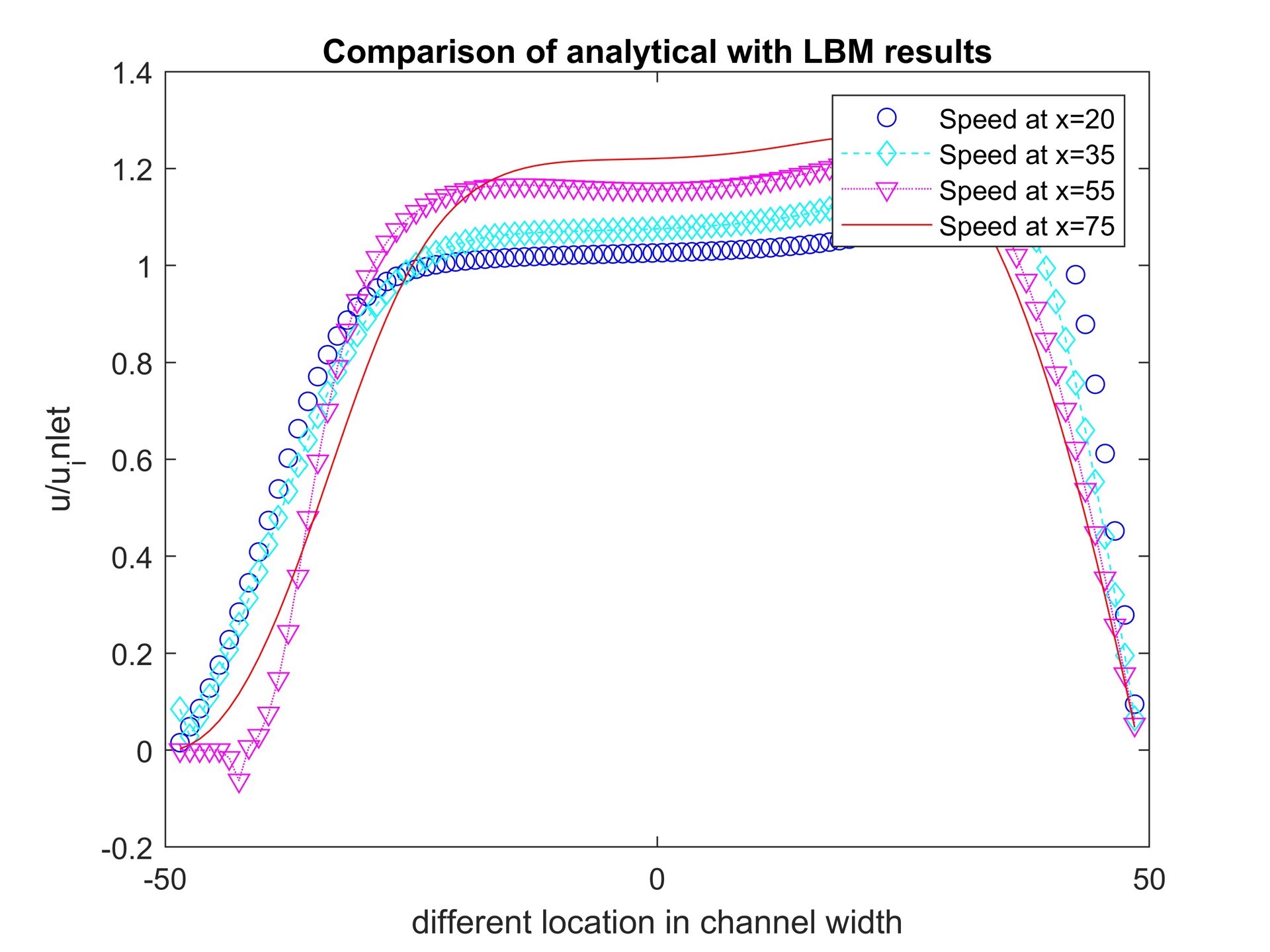





















 1344
1344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








