机器学习教学基础之python矩陈运算

最新推荐文章于 2022-01-18 17:39:57 发布

原创最新推荐文章于 2022-01-18 17:39:57 发布 · 185 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了机器学习中的基础概念——梯度下降法，详细讲解了微分理解、梯度的概念，并提供了数学解释。通过手动求解和Python编程演示了梯度下降法如何寻找函数最小值的过程，最后展示了数据变化和迭代结果的绘制。

1 梯度下降法

参考链接：梯度下降法(Gradient Descent) – 现代机器学习的血液

2 微分理解

1、我们所要优化的函数必须是一个连续可微的函数，可微，既可微分，意思是在函数的任意定义域上导数存在。如果导数存在且是连续函数，则原函数是连续可微的。
2、函数图像中，某点的切线的斜率
3、函数的变化率
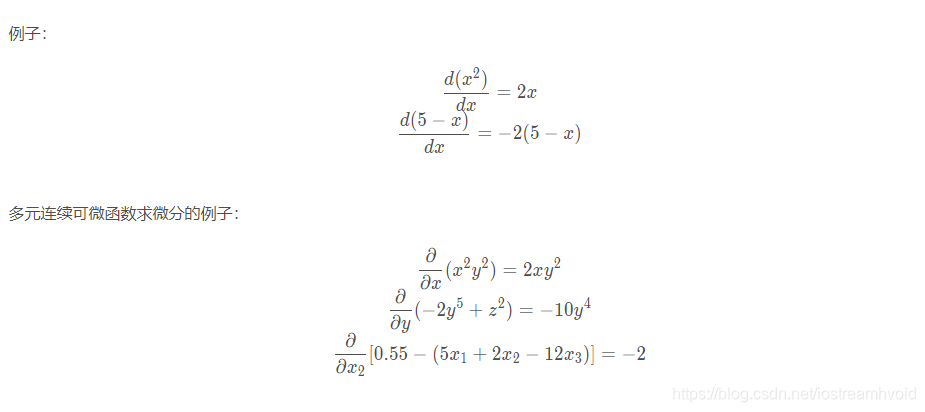
在这里插入图片描述

3 梯度理解

在这里插入图片描述

4 数学解释

深入浅出–梯度下降法及其实现

5 手工求解

问题描述：
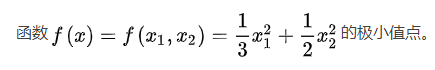
在这里插入图片描述
计算过程：

6 演示梯度下降法的数据变化

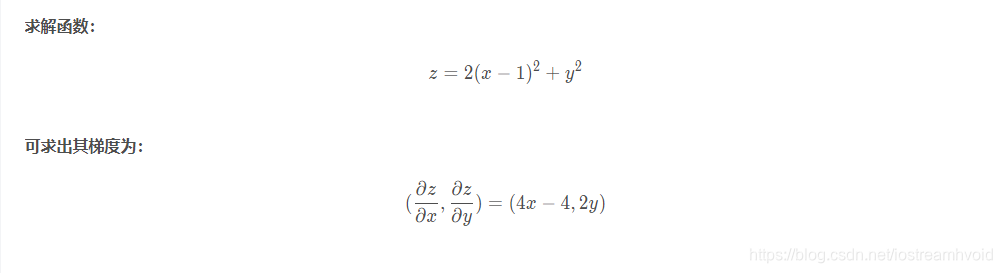
在这里插入图片描述

初始设定
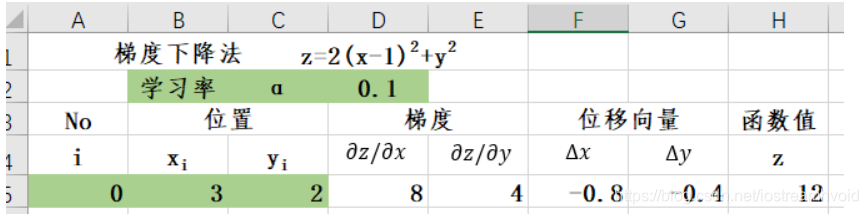
计算位移量

在这里插入图片描述

更新位置
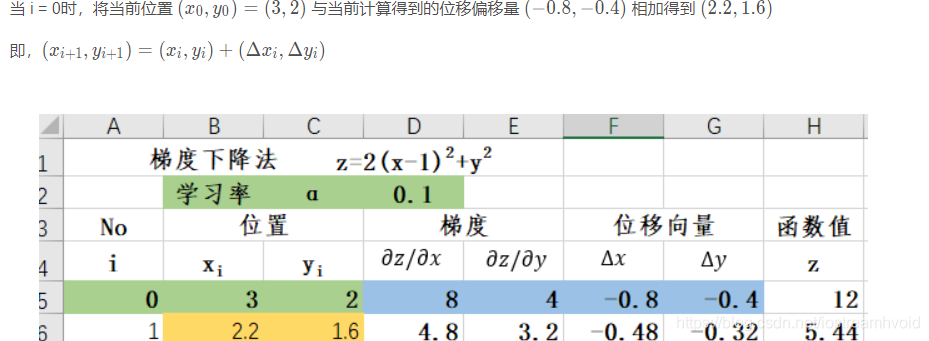
反复执行2和3的操作

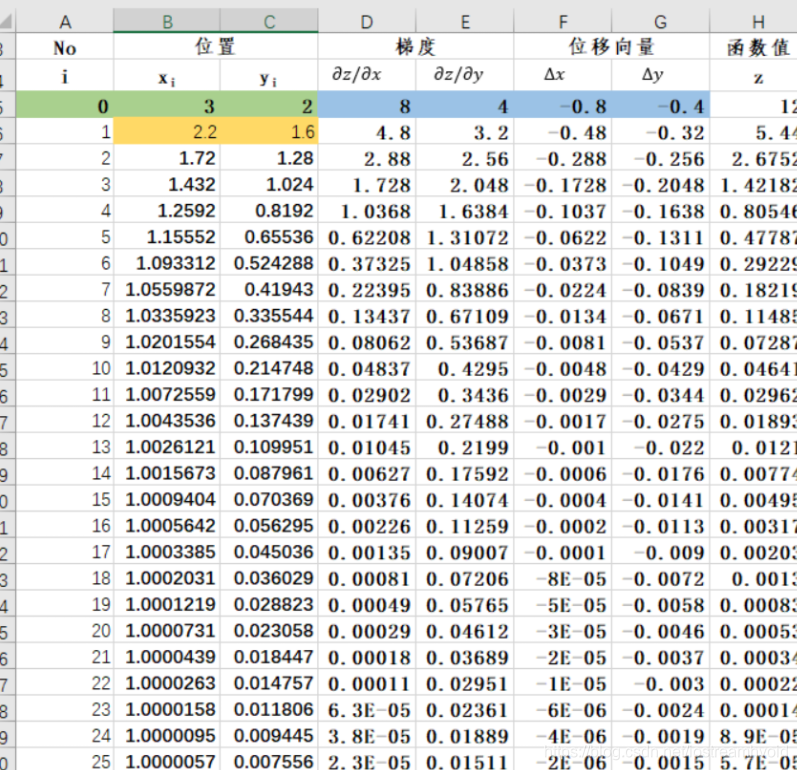
在这里插入图片描述

函数 z zz 在 (1,0) 处取得最小值 0

7 Python 编程

导入所需库

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings

函数定义

def Z(x,y):
   return 2*(x-1)**2 + y**2
# x方向上的梯度
def dx(x):
   return 4*x-4
# y方向上的梯度
def dy(y):
   return 2*y

赋初值

X = x_0 = 3
Y = y_0 = 2
# 学习率
alpha = 0.1

定义数据保存列表

globalX = [x_0]
globalY = [y_0]
globalZ = [Z(x_0,y_0)]

重复迭代30次

for i in range(30):
    temX = X - alpha * dx(X)
    temY = Y - alpha * dy(Y)
    temZ = Z(temX, temY)
    # X,Y 重新赋值
    X = temX
    Y = temY
    # 将新值存储起来
    globalX.append(temX)
    globalY.append(temY)
    globalZ.append(temZ)

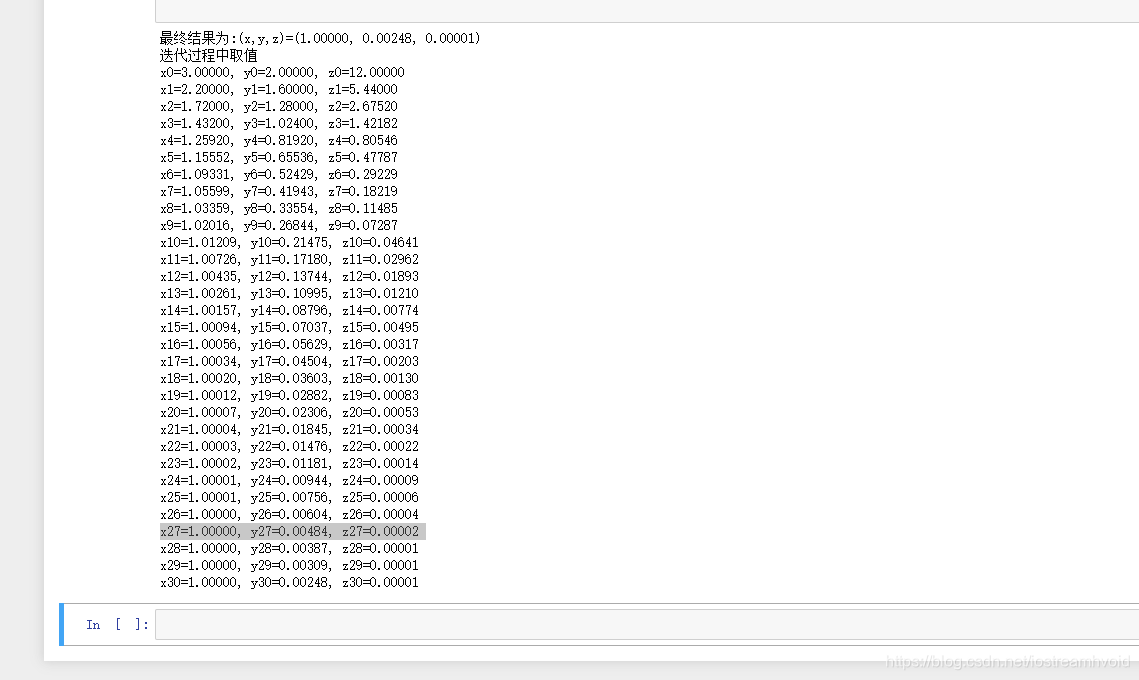
打印结果

print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f)" % (X, Y, Z(X,Y)))
print(u"迭代过程中取值")
num = len(globalX)
for i in range(num):
    print(u"x%d=%.5f, y%d=%.5f, z%d=%.5f" % (i,globalX[i],i,globalY[i],i,globalZ[i]))

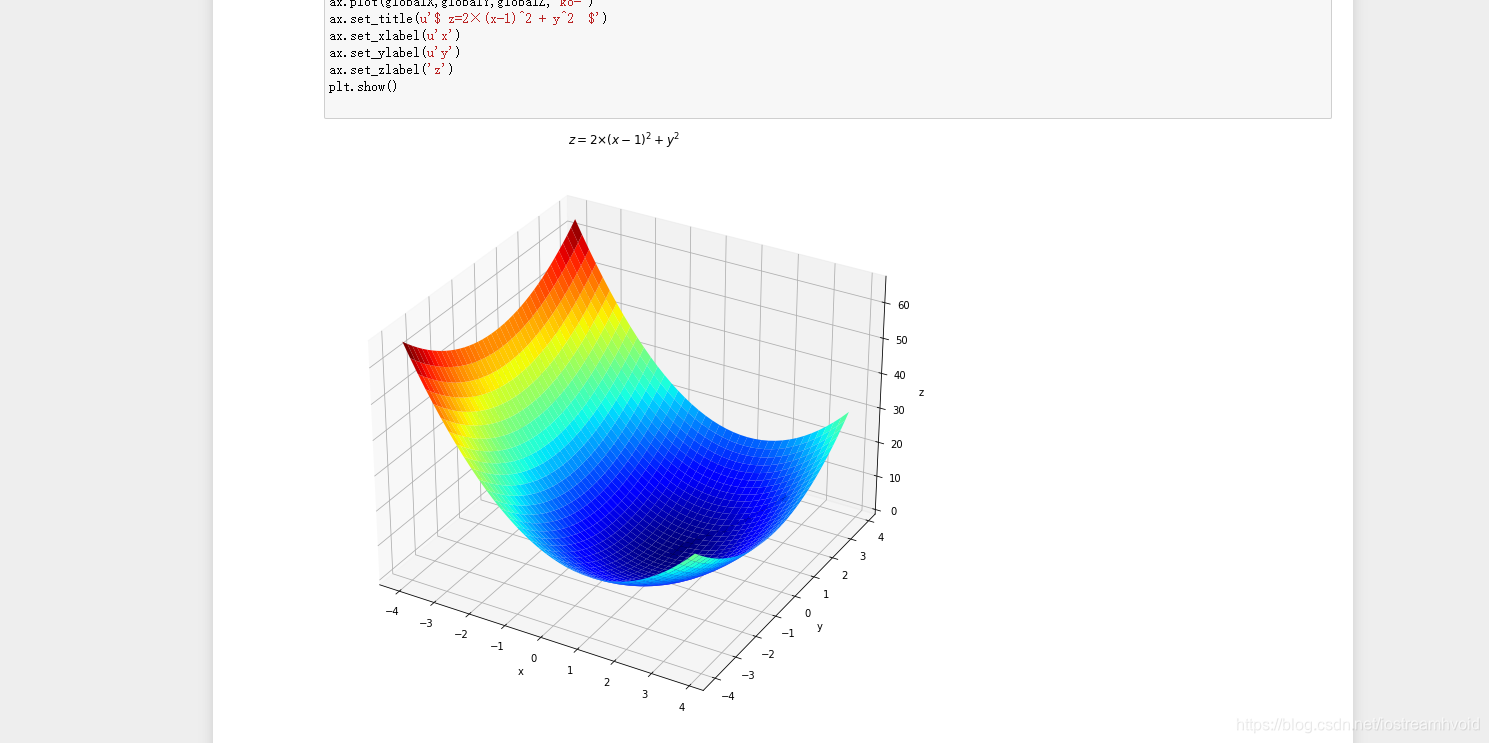
在这里插入图片描述

绘制过程图

axisX = np.arange(-4,4,0.2)
axisY = np.arange(-4,4,0.2)
axisX, axisY = np.meshgrid(axisX, axisY) # 生成xv、yv，将axisX、axisY变成n*m的矩阵，方便后面绘图
valueZ = np.array(list(map(lambda t : Z(t[0],t[1]),zip(axisX.flatten(),axisY.flatten()))))
valueZ.shape = axisX.shape # 1600的Z图还原成原来的（40,40）
%matplotlib inline

#作图
fig = plt.figure(facecolor='w',figsize=(12,8))
ax = Axes3D(fig)
ax.plot_surface(axisX,axisY,valueZ,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(globalX,globalY,globalZ,'ko-')
ax.set_title(u'$ z=2×(x-1)^2 + y^2  $')
ax.set_xlabel(u'x')
ax.set_ylabel(u'y')
ax.set_zlabel('z')
plt.show()
';

在这里插入图片描述