sklearn 5.18.10 logistic function

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from scipy.special import expit

# 本例子生成100个随机样本，样本转换为数据矩阵，根据样本的正负值生成目标值y，样本值为整，则目标值为1，样本值为负，则目标值为0
# 实例化logistic regression模型，训练模型
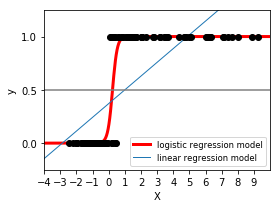
# 将原始数据集可视化为散点图，用黑色标出
# 创建测试数据集，-5到10的等差数列，共300个样本
# 可视化测试数据乘以相关系数加上截距后的值，用红色标出
# 实例化linear regression模型，训练模型
# 可视化测试数据乘以相关系数加上截距后的值，用默认的蓝色标出
# 画y=0.5的线，表示分类的分隔线，用灰色标出
# 因为本例中目标值是0和1，所以分隔线是y=0.5，如果目标值是-1和1，那分隔线是y=0
xmin, xman = -5, 5
n_samples = 100
np.random.seed(0)
X = np.random.normal(size=n_samples)
# 类型转换，True变为1.0，False变为0.0
y = (X>0).astype(np.float)
X[X>0]*=4
X+=0.3 * np.random.normal(size=n_samples)
# 添加新列，将X的形状从（100，）变为（100,1）
X = X[:,np.newaxis]
# fit the classifier
clf = linear_model.LogisticRegression(C=1e5, solver='lbfgs')
clf.fit(X, y)
# plot the result
plt.figure(1, figsize=(4,3))
plt.clf()
plt.scatter(X.ravel(), y, color='black', zorder=20)
X_test = np.linspace(-5, 10, 300)
# expit函数就是logistic sigmoid函数，用来计算分类
loss = expit(X_test*clf.coef_+clf.intercept_).ravel()
plt.plot(X_test, loss, color='red', linewidth=3)
ols = linear_model.LinearRegression()
ols.fit(X,y)
plt.plot(X_test, ols.coef_*X_test+ols.intercept_, linewidth=1)
plt.axhline(0.5, color='.5')
plt.ylabel('y')
plt.xlabel('X')
plt.xticks(range(-5, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-0.25, 1.25)
plt.xlim(-4, 10)
plt.legend(['logistic regression model', 'linear regression model'], loc='lower right', fontsize='small')
plt.tight_layout()
plt.show()