sklearn 5.18.9 polynomial interpolation

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
# 整个流程大致如下：
# 生成两个一样的等差数列x和x_plot，取值范围从0到10，共100个元素
# 重排x的数据，然后取出x数组前20行样本，再将这20个样本排序，返回新的x数组
# 使用函数f基于新x数组生成y数组，即目标值
# 把新x转换成（20,1）的矩阵，返回X，同理转换x_plot为矩阵，返回X_plot
# 在图上画出x_plot和f(x_plot)，即生成训练数据的等差数列和目标值
# 再在图上画出取出来的20个样本点
# 循环使用多项式特征生成的训练样本训练岭回归
# 使用管道函数，将多项式特征生成与训练模型组成管道，简化编码
# 管道基于矩阵X和y训练模型
# 再使用训练过的模型预测矩阵数据X_plot，得到预测值y_plot
# 在图中画出测试数据X_plot和预测值y_plot
# 训练中的训练变量是用于多项式生成类的度，度决定了多项式转换后的特征数量，度越大，转换后的训练数据特征数目越多
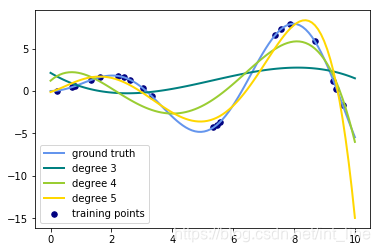
# 从结果图中可以看出来，度越高，特征越多，对测试数据的拟合度越好，但模型越复杂，所以需要根据场景在泛化能力和模型复杂度之间进行权衡
# function to approximate by polynomial interpolation
def f(x):
    return x*np.sin(x)
# generate points used to plot
x_plot = np.linspace(0, 10, 100)
# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
# np.random模块下的重排函数，把数据x样本顺序重排，但不改变样本内容，只能重排索引顺序，不能重排特征熟悉怒
rng.shuffle(x)
# 取出x数组前20行数据，并返回排序后的数组
x = np.sort(x[:20])
y = f(x)
# create matrix versions of these arrays
# X的size为（20,1）
X = x[:, np.newaxis]
# X_plot的size为（100,1）
X_plot = x_plot[:, np.newaxis]
colors = ['teal', 'yellowgreen', 'gold']
lw = 2
plt.plot(x_plot, f(x_plot), color='cornflowerblue', linewidth=lw, label='ground truth')
plt.scatter(x, y, color='navy', s=30, marker='o', label='training points')
for count, degree in enumerate([3,4,5]):
    model = make_pipeline(PolynomialFeatures(degree), Ridge())
    model.fit(X,y)
    y_plot = model.predict(X_plot)
    plt.plot(x_plot, y_plot, color=colors[count], linewidth=lw, label='degree %d' % degree)
plt.legend(loc='lower left')
plt.show()

print(x.shape)
print(X.shape)
print(y.shape)
print(x_plot.shape)
print(X_plot.shape)
print(y_plot.shape)

(20,)
(20, 1)
(20,)
(100,)
(100, 1)
(100,)