1~4字节的CRC32非暴力破解，在线工具手工计算

0. 前言

CRC校验设计的目的是用于低误比特率信道下的数字信息传输差错检测，以及部分数字存储信息的损坏检测，并非加密算法。不知为何，网上有很多研究CRC32暴力破解的文章，即根据原数据的校验码和原数据的长度，把相同长度如4字节（则可能有\( 2^{32} \)个原始数据），采用穷举（暴力）的方式，看哪个数据算得的校验码和已知校验码相等，则把该数据作为原始数据的破解值。

看大家乐此不疲，算得又累，本文给出一个可以利用如ip33这样的在线CRC计算工具，在已知原数据长度（1~4字节）和校验码的条件下，手工破解的方法。本文只给出直接的计算步骤，不讨论相关原理。

1. 计算模型及步骤

文件压缩软件WinRAR的CRC-32校验与以太网的CRC-32/IEEE 802.3一致，计算模型的参数如下：

• 宽度WIDTH                                ：32；
• 多项式POLY(HEX)                     ：04C11DB7；
• 初始值INIT(HEX)                        ：FFFFFFFF；
• 结果异或值XOROUT(HEX)        ：FFFFFFFF；
• 输入数据反转REFIN                   ：True；
• 输出数据反转REFOUT               ：True。

对于1~4字节的数据，无需暴力破解。即知道数据的长度（1~4字节）和它的校验码，利用ip33在线工具即可手工反算该数据内容。

第一步，计算CRC-32/IEEE 802.3校验码生成多项式的反多项式，结果用作逆向计算的多项式。POL 0x04C11DB7的反多项式为0xDB710641，如下图所示（此步骤干一次进行了，下次直接用）：

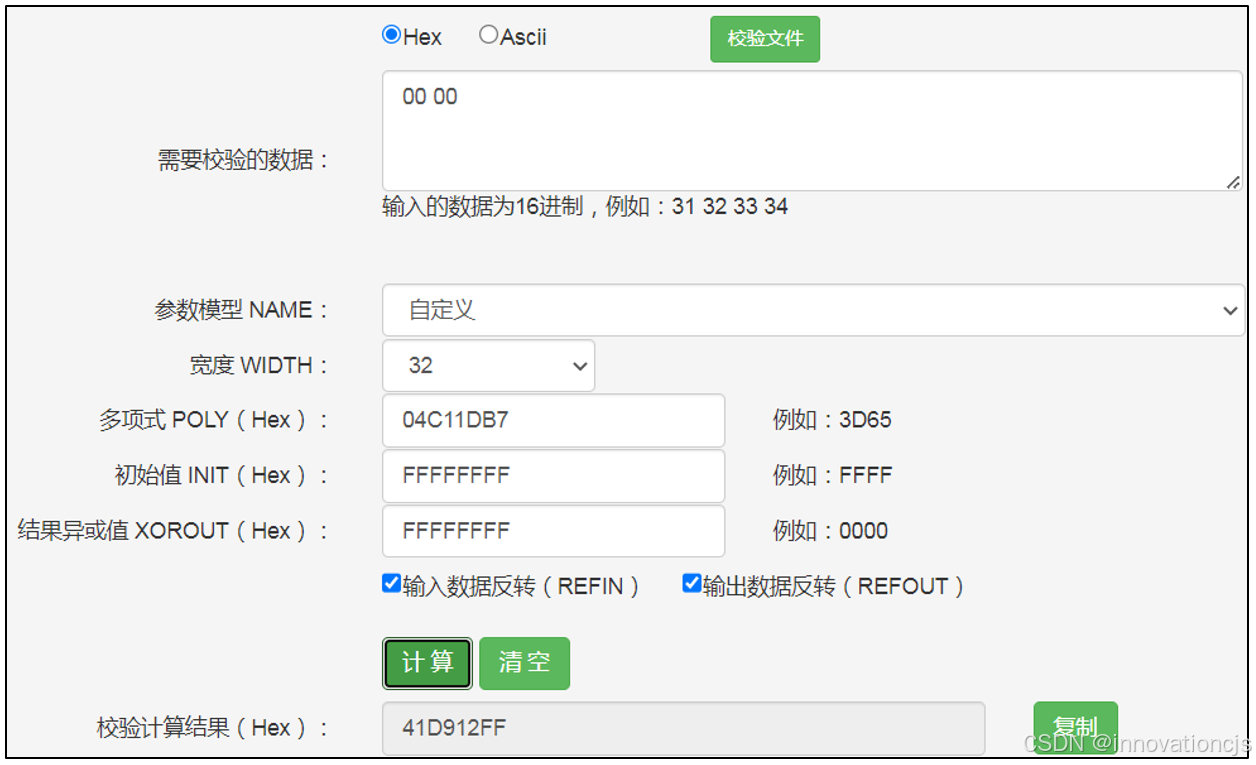
第二步，计算逆运算模型的初始值（本步骤也是预计算步骤，干一次就行了）。不同数据长度时，该初始值不同。本文限定1~4字节数据，需提前计算4个初值。1字节时，将0x00作为数据，代入CRC-32/IEEE 802.3原始模型计算结果，该结果作为1字节数据逆运算模型的初值；2字节时，CRC-32/IEEE 802.3原始模型的输入为0x0000，结果为2字节逆运算模型的初值；依次类推，共计算4个初值备用：1字节逆运算初值0xD202EF8D；2字节逆运算初值0x41D912FF；3字节逆运算初值0xFF41D912；4字节逆运算初值0x2144DF1C。计算方法如下图所示：

第三步，以原数据的校验码为输入数据，代入逆运算模型计算结果。结果始终是4字节的，需要根据确定的原数据长度，从右至左取相应长度的数据即为逆运算出的原始数据。逆运算计算模型如下：

• 宽度WIDTH                                 ：32；
• 多项式POLY(HEX)                      ：DB710641；
• 初始值INIT(HEX)                         ：根据原数据长度选择；
• 结果异或值XOROUT(HEX)         ：00000000；
• 输入数据反转REFIN                    ：False；
• 输出数据反转REFOUT                ：False。

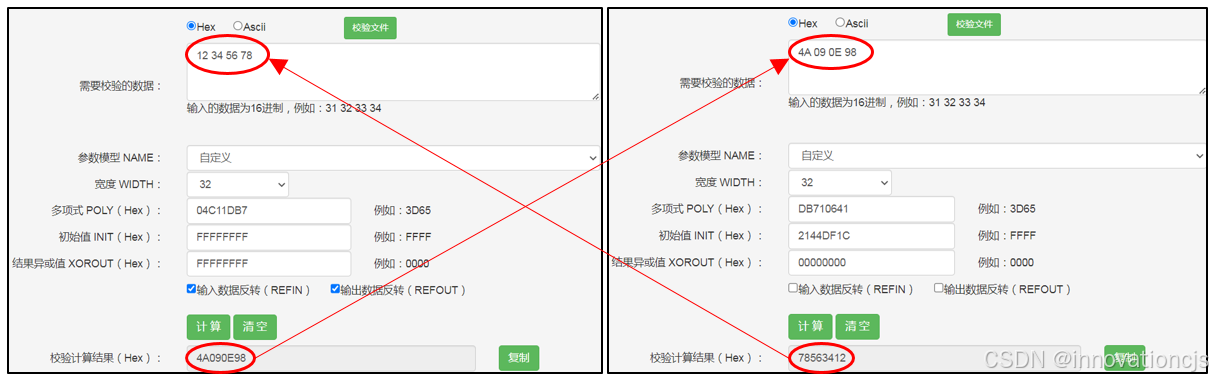
以原始数据为0x12345678为例，校验码为0x4A090E98，把校验码作为输入代入4字节逆运算模型的计算结果为0x78563412，按字节反过来看就是原始数据，如下图所示：

2. 网友案例复现

以优快云网友@Nobody Anyone的博文《浅谈使用Python脚本爆破CRC32》为例，复现该文1、2、3、4字节案例中的首个数据。

2.1 单字节破解实例

文章单字节破解实例的首个数据是大写字符“M”，对应的16进制数据是0x4D，原数据的校验码是0xDA6FD2A0。手工破解如下（逆运算模型初值：0xD202EF8D）：

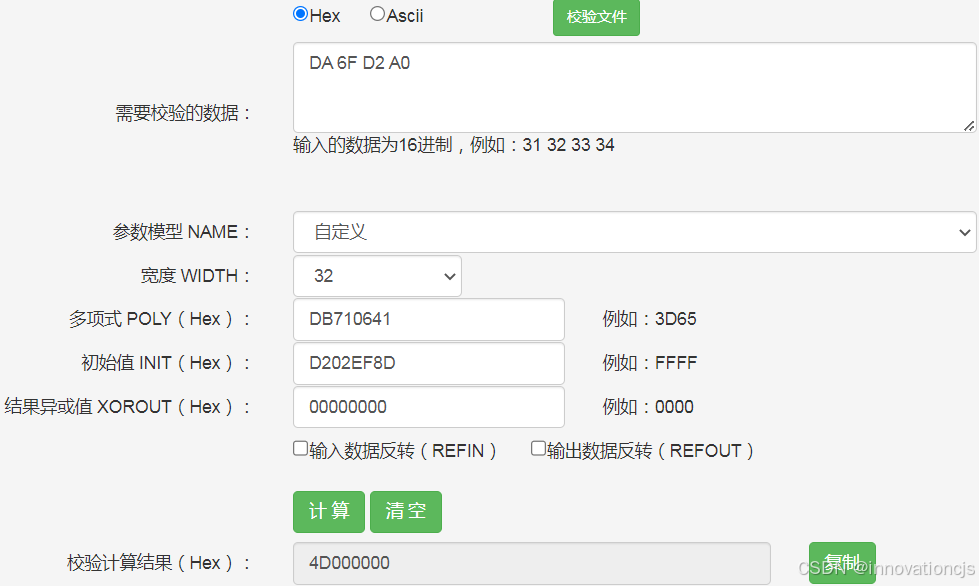
计算结果0x4D000000，已知原数据是单字节的，取最高字节0x4D作为破解结果。

2.2 双字节破解实例

文章双字节破解实例的首个数据是字符“$9”，对应的16进制数据是0x2439，原数据的校验码是0xEF347B51。手工破解如下（逆运算模型初值：0x41D912FF）：

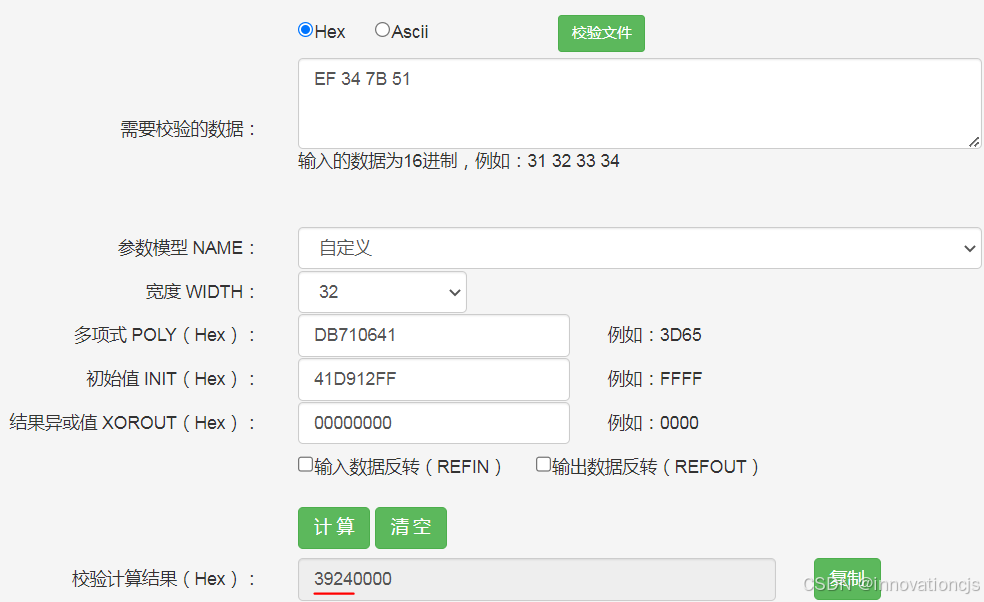
计算结果是0x39240000，已知原数据是双字节的，取最高两个字节0x3924作为破解结果。注意按字节反过来看，即破解所得数据为0x2439。

2.3 三字节破解实例

文章三字节破解实例的首个数据是字符“Z&9”，对应的16进制数据是0x5A2639，原数据的校验码是0x02B17958。手工破解如下（逆运算模型初值：0xFF41D912）：

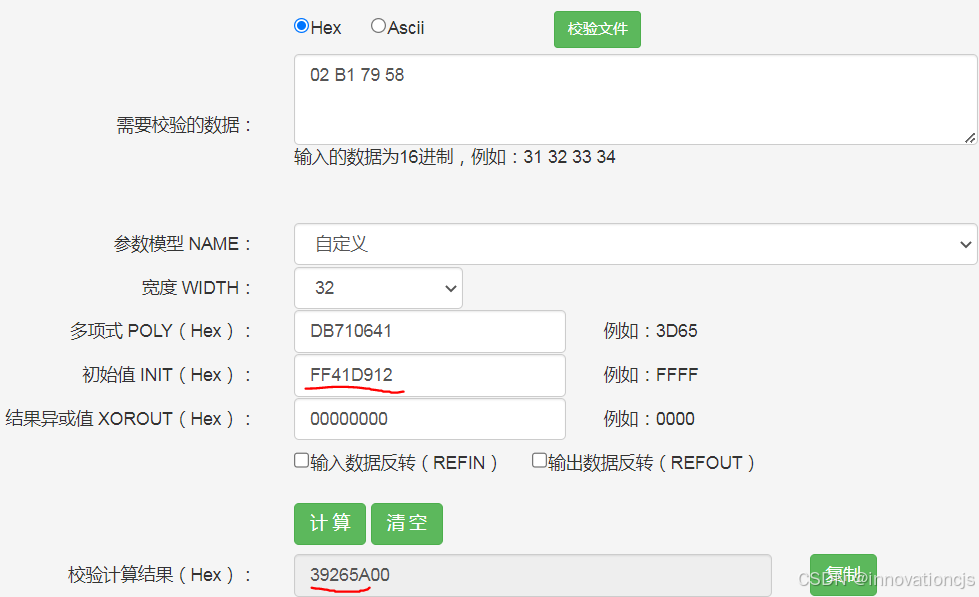
计算结果是0x39265A00，已知原数据是三字节的，取高三个字节0x39265A，再按字节倒过来看，即0x5A2639，获得正确的破解结果。

2.4 四字节破解实例

文章四字节破解实例的首个数据是字符“T9^n”，对应的16进制数据是0x54395E6E，原数据的校验码是0xC0A3A573。手工破解如下（逆运算模型初值：0x2144DF1C）：

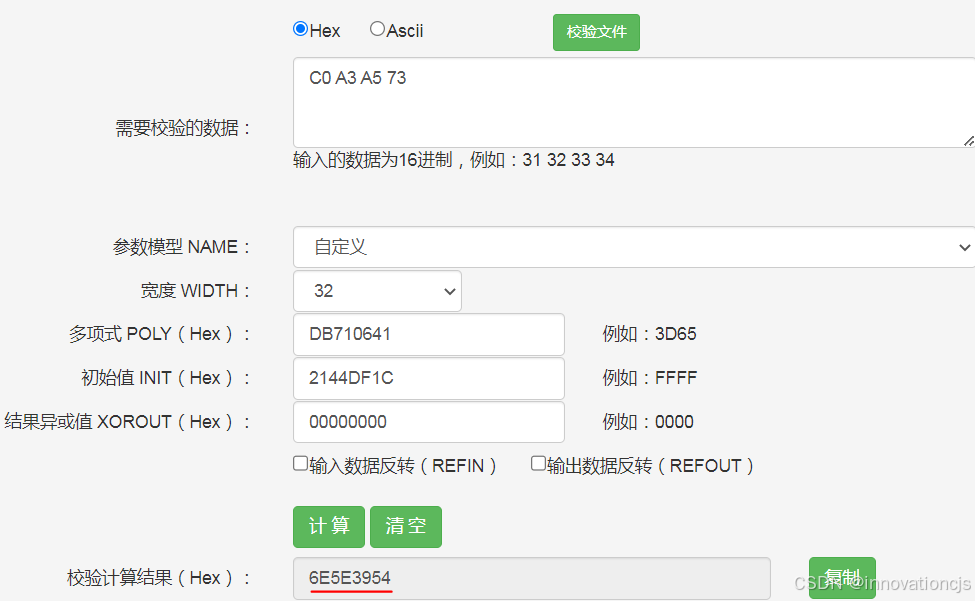
计算结果是0x6E5E3954，按字节倒过来看即为正确的破解结果：0x54395E6E。

3. 总结

不要问我4字节以上怎么算，例如5字节，有\( 2^8=256 \)个原数据对应同一个校验码，6字节有65536个，7字节有\( 2^{24}=16,777,216 \)个......咋办，我目前能想到的还是只有猜。