数据结构---图

1.01 图

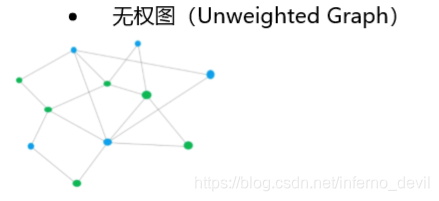
图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中，图是最灵活的数据结构之一，很多问题都可以使用图模型进行建模求解。
例如：生态环境中不同物种的相互竞争、人与人之间的社交与关系网络、化学上用图区分结构不同但分子式相同的同分异构体、分析计算机网络的拓扑结构确定两台计算机是否可以通信、找到两个城市之间的最短路径等等。

图的两个重要组成部分

• 结点Vertex
• 边Edge
  
  可以表示：交通运输，社区网络，互联网，工作安排，脑区活动，程序状态执行。

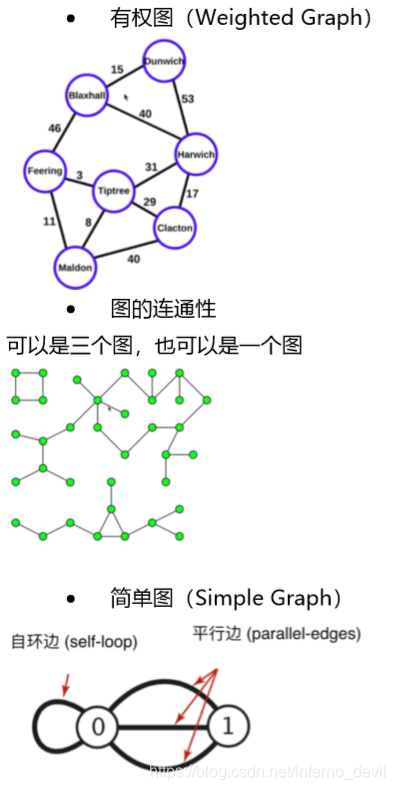
图的分类

• 无向图
  
• 有向图
  
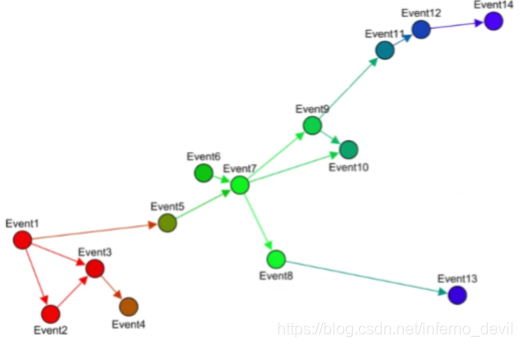
  我们主要以无向图为主，无向图是一种特殊的有向图，所以讲来讲解的都是通用的操作
  
  
  
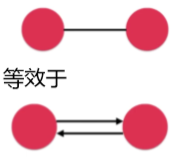
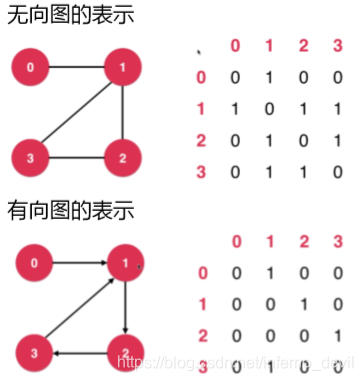
  图的表示
• 链接矩阵，用矩阵的方式表示图
  
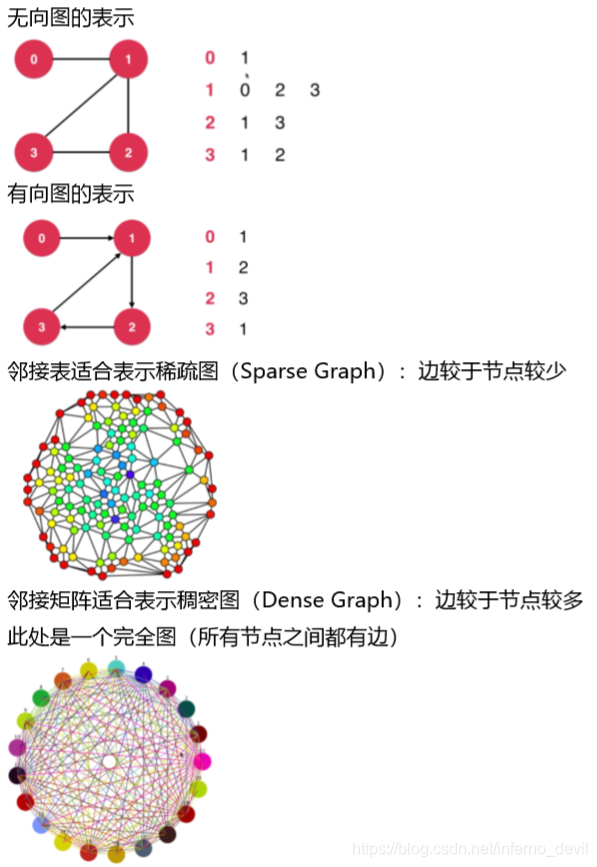
• 邻接表，类似哈希表
  
  Graph接口的定义

public interface Graph{
	public int V();	//返回节点个数
	public int E();	//返回边的个数
	public void addEdge(int v,int w);	//想图中添加一个边v-w或者v->w
	boolean hasEdge(int v,int w);	//验证图中是否有v到w的边
	void show();	//将图打印出来
	public Iterable<Integer> adj(int v);	//返回图中一个顶点的所有邻边
}

稠密图——邻接矩阵DenseGraph
//稠密图——邻接矩阵

public class DenseGraph implements Graph{
private int n; //节点数
private int m; //边数
private boolean directed;//是否为有向图
private boolean[][] g; //图的具体数据
//构造函数
public DenseGraph(int n,boolean directed){
if(n<0){
throw new IllegalArgumentExceptiion(“节点个数不能小于零！”);
}
this.n=n;
this.m=m; //初始化没有任何边
this.directed=directed;
//g初始化为n*n的布尔矩阵，每一个g[i][j]均为false。表示没有任何边
//false为Boolean型变量的默认值
g=new boolean[n][n];
}

//返回节点个数
public int V(){
	return n;
}

//返回边的个数
public int E(){
	return m;
}

//像图中添加一个边v-w或者v-w不管平行边
public void addEdge(int v,int w){
	if(v<0&&v>=n){
		throw new IllegalArgumentException("角标越界！");
	}
	if(w<0&&w>=n	){
		throw new IllegalArgumentException("角标越界！");
	}
	//先判断是否已经有边
	if(hasEdge(v,w))
		return;
	g[w][v]=true;	//有向图-单向
	if(!directed)
		g[w][v]=true;	//无向图-双向
	m++;
}

//验证图中是否有v到w的边
public boolean hasEdge(int v,int w){
	if(v<0&&v>=n){
		throw new IllegalArgumentException("角标越界");
	}
	if(w<0&&w>=m){
		throw new IllegalArgumentException("角标越界！");
	}
	return g[v][w];
}
//返回图中一个顶点的所有邻边
public Iterable<Integer>adj(int v){
	if(v<0&&v>=n){
		throw new IllegalArgumentException("角标越界");
	}
	Vector<Integer> adjV=new Vector<Integer>();
	for(int i=0;i<n;i++){
		if(g[v][i])
			adjV.add(i);
		return adjV;
	}
	
	public void show(){
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				System.out.print((g[i][j]==true?1:0)+" ");
			System.out.println();
			}
		}
	}

稀疏图——邻接表SparseGraph