数据结构---红黑树（RBTree）

1.01 红黑树

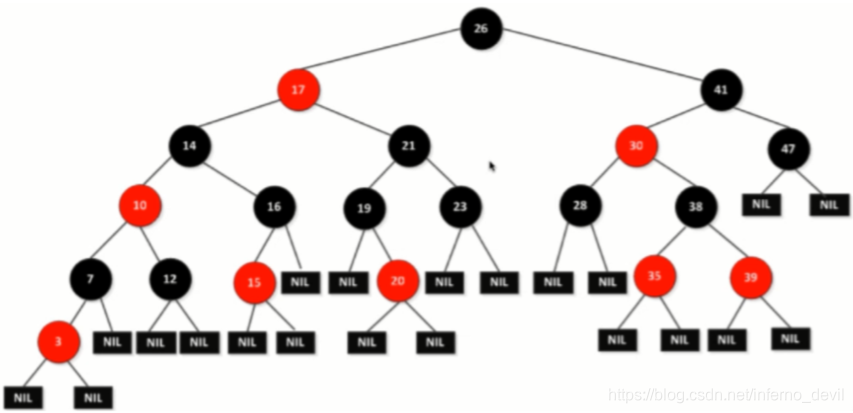
-红黑树是每个节点都带有颜色属性的二叉搜索树，颜色或红色或黑色。
-红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。
-红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。
-它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

1.02 2-3树
学习2-3树，不仅对于理解红黑树有帮助，对于理解B类树，也是有巨大帮助的。
B类树（文件系统，磁盘存储，数据库）

2-3树性质：

满足二分搜索树的基本性质
其本身不是二叉树
结点可以存放一个元素或者两个元素
结点有两个孩子或者三个孩子

2-3树，如图：

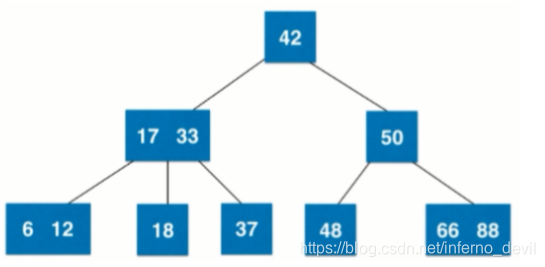
注意：2-3树是一种绝对平衡的树，从根节点到任意叶子结点所经过的节点数一定相同。

1.03 红黑树

红黑树和2-3树是等价性
（换句话说，对于每个 2-3-4 树，都存在至少一个数据元素是同样次序的红黑树。在 2-3-4 树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。这使得 2-3-4 树成为理解红黑树背后的逻辑的重要工具，这也是很多介绍算法的教科书在红黑树之前介绍 2-3-4 树的原因，尽管 2-3-4 树在实践中不经常使用。）

代码实现2-3树比较复杂，因为既要操作2结点还要操作3结点，没有像之前统一操作结点方便，所以产生出红黑树。

性质：

在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1. 每个节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
性质5.每个节点的叶子结点（最后的空结点）默认是黑色的。

最大高度：2logn
时间复杂度：O（logn）
相对于AVL而言，插入元素和删除元素更加便捷。

注意：严格意义讲红黑树不是平衡二叉树，是一个对于其黑结点绝对平衡的树。

红黑树中添加新元素：

2-3树中添加一个新元素

• 添加到2结点，形成3结点
• 添加到3结点，暂时形成4结点，在拆解
  所以，新来的元素总要和当前叶子结点融合，所以永远新元素为红色
  但是根节点必须是黑色的。

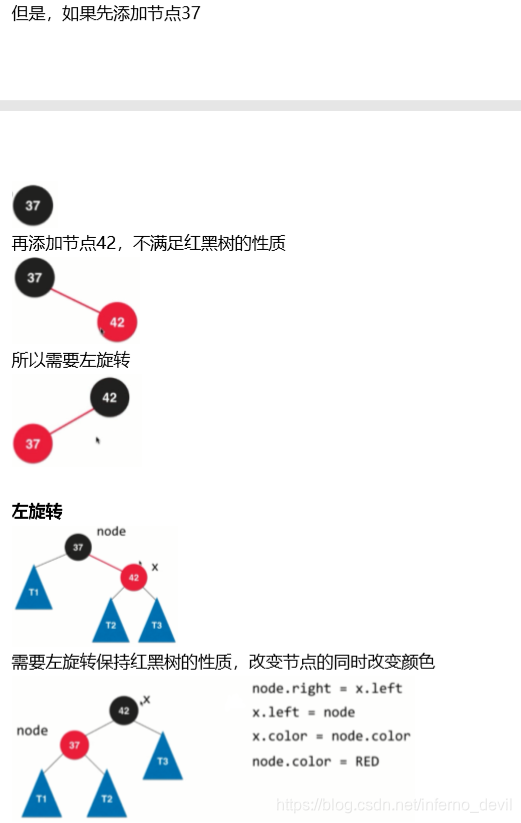
情况1 插入比根节点小的元素

情况2 插入比根节点大的元素

情况3 已有3结点时，插入比根节点大的元素

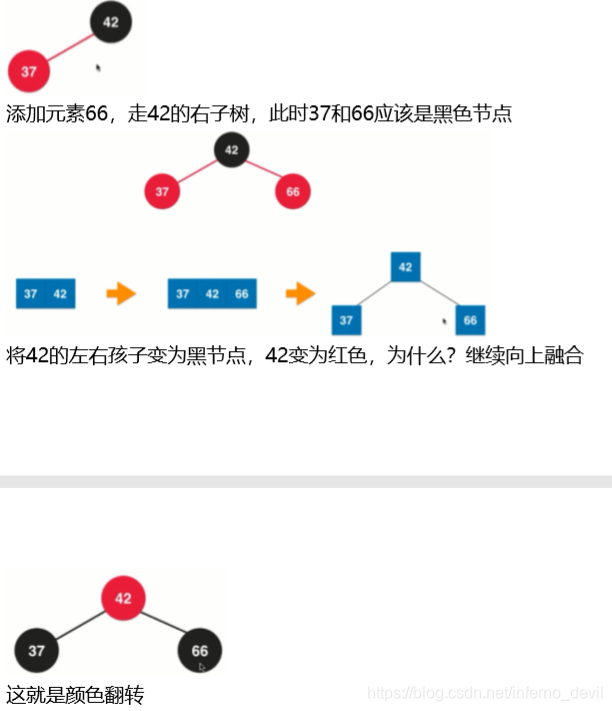
情况4 已有3结点时，插入最小元素

情况5 已有3结点时，插入中等元素

总结：

对于完全随机的数据，普通的二分搜索树很好用！
缺点：极端情况退化成链表（或者高度不平衡）

对于插叙较多的使用情况，AVL树很好用!
红黑树牺牲了平衡性（2logn的高度）

红黑树统计性能更优（总和增删改查所有的操作）
还有类似的SplayTree伸展树