数据结构---并查集

1.01 并查集：

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

转的一个超级有意思，好懂的并查集解释， 膜拜大神~~

并查集：由孩子指向父亲的树结构，主要解决连接问题

网络中结点的连接状态

网络是一个抽象的概念：

• 用户之间形成的社交网络
• 商品，图书，音乐，火车…很多很多
• 数学中的集合类实现 并集 查询

连接问题和路径问题：

• 连接相对于路径个那个如简单 只需回答是否连接
• 路径相对于连接更为复杂，先找路，后判断连接

对于一组数据，主要支持两个动作：

• union(p,q)
• isConnected(p,q)

并查集的基本数据表示

1.02 UnionFind并查集接口定义

public interface UnionFind{
	int getSize();	//一共考虑多少个元素 不关心增加和删除
	boolean isConnected(int p,it q);	//两个元素是否可连接 不关心具体元素 当做角标处理
	void unionElements(int p,int q);	//将两个元素并在一起
}

1.03 UnionFind1类定义（用数组模拟并查集）

public class UnionFind1 implments UnionFind{
	private int[] id;
	public UnionFind1(int size){
		id=new int[size];
		for(int i=0;i<id.length;i++){
			id[i]=i;	//每个元素一个集合
		}
	}
	
	public int getSize(){
		return id.length;
	}

	private int find(int p){
		if(p<0||p>=id.length){
			throw new IllegalArgumentException("p is out of bound");	//越界
		}
		return id[p];
	}

	public boolean isConnected(int p,int q){
		return find(p)==find(q);
	}

	public void unionElements(int p,int q){	//将两个元素连接
		int pID=find(p);
		int qID=find(q);
		if(pID==qID){
			return;
		}
		for(int i=0;i<id.length;i++){
			if(id[i]==pID){
				id[i]=qID;
			}
		}
	}
}

基于时间复杂度的优化：

UnionFind1仅仅是用数据模拟一个并查集的操作，但是最好将每一个元素，看做是一个结点。

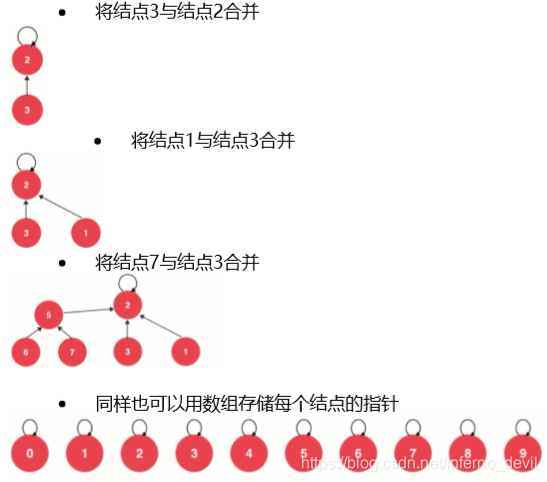
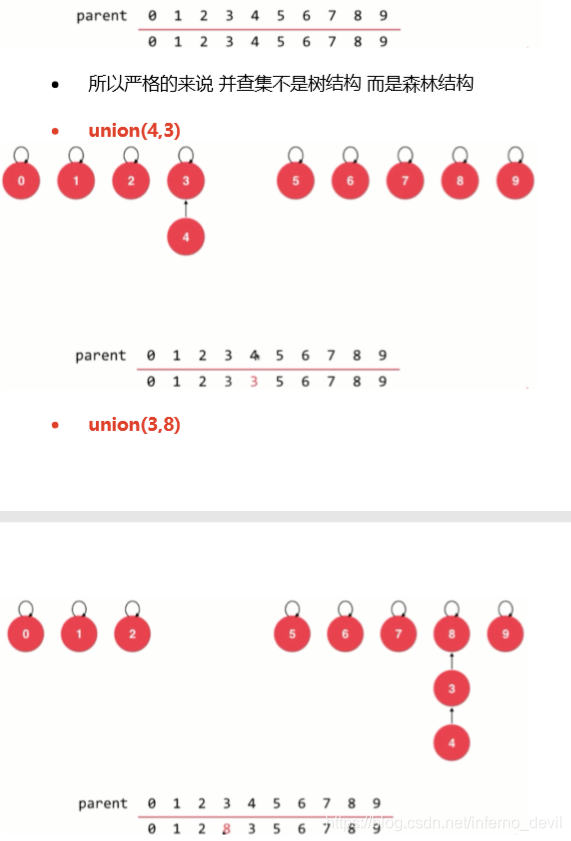
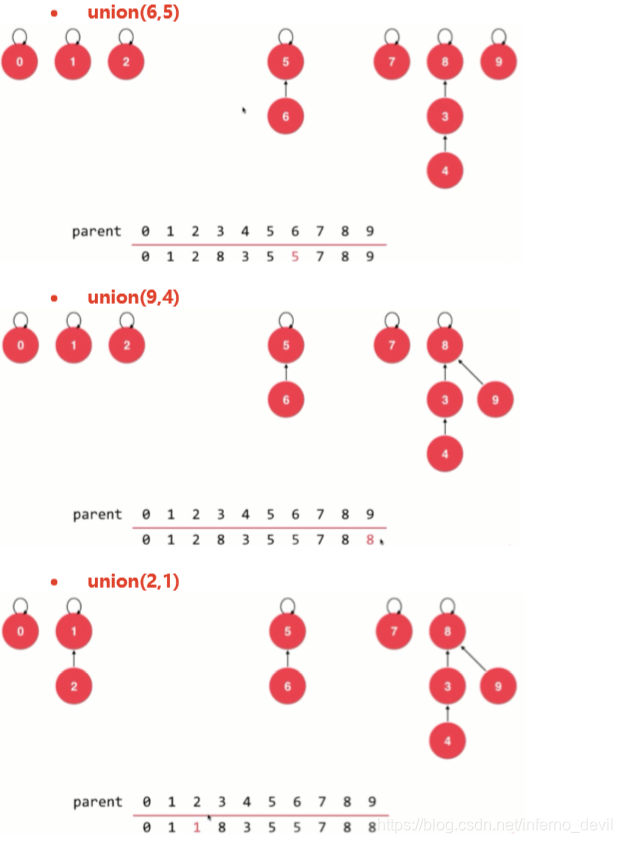
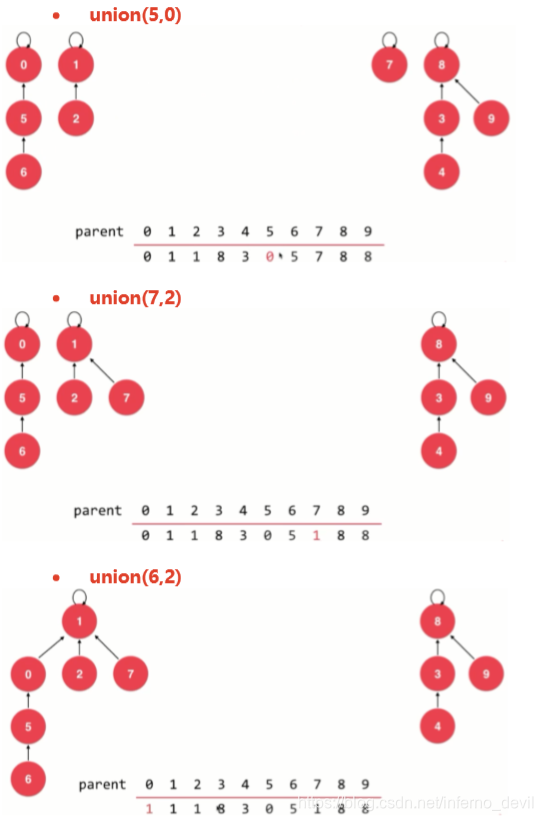
UnionFind2类定义（优化时间复杂度）

public class UnionFind2 implements UnionFind{
	private int[] parent;
	public UnionFind2(int size){
		parent=new int[size];
		for(int i=0;i<size;i++){
			parent[i]=i;
		}
	}

	public int getSize(){
		return parent.length;
	}
	
	private int find(int p){
		if(p<0||p>=parent.length){
			throw new IllegalArgumentException("p is out of bound");
		}
		while(p!=parent[p]){
			p=parent[p];
		}
		return p;
	}

	public boolean isConnected(int p,int q){
		return find(p)==find(q);
	}

	public void unionElements(int p,int q){
		int pRoot=find(p);
		int qRoot=find(q);
		if(pRoot==qRoot){
			return;
		}else{
			parent[pRoot]=qRoot;
		}
	}
}

基于size的优化：

但是对于其实现而言，可能最终退化成一个链表。

UnionFind3类定义（优化深度）

public class UnionFind3 implements UnionFind{
	private int[] parent;
	private int[] sz;
	public UnionFind3(int size){
		parent=new int[size];
		sz=new int[size];
		for(int i=0;i<size;i++){
			parent[i]=i;
			sz[i]=1;
		}
	}

	public int getSize(){
		return parent.length;
	}
	
	private int find(int p){
		if(p<0||p>=parent.length){
			throw new IllegalArgumentException("p is out of bound");
		}
		while(p!=parent[p]){
			p=parent[p];
		}
		return p;
	}

	public boolean isConnected(int p,int q){
		return find(p)==find(q);
	}

	public void unionElements(int p,int q){
		int pRoot=find(p);
		int qRoot=find(q);
		if(pRoot==qRoot){
			return;
		}
		//根据两个元素所在树的元素个数不同判断合并方向
		//将元素个数绍的集合合并到元素个数多的集合上
		if(sz[pRoot]<sz[qRoot]){
			parent[pRoot]=qRoot;
			sz[qRoot]+=sz[pRoot];
		 }else{
		 	parent[qRoot]=pRoot;
		 	sz[pRoot]+=sz[qRoot];
		 }
	}
}

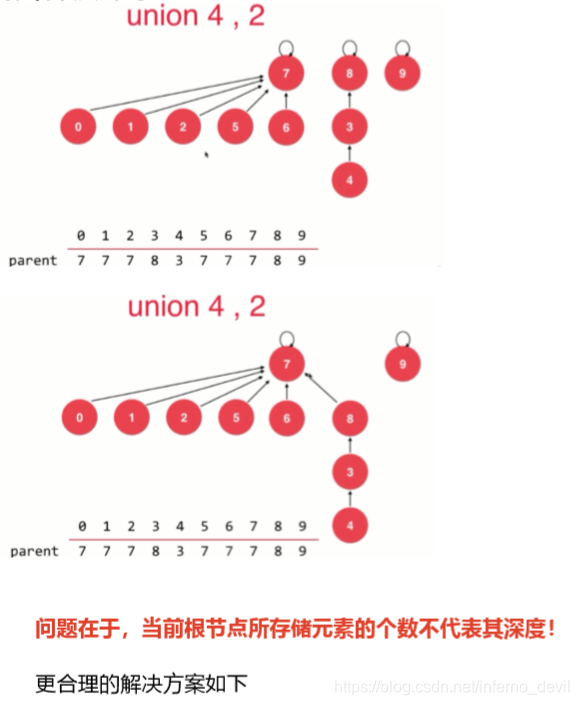
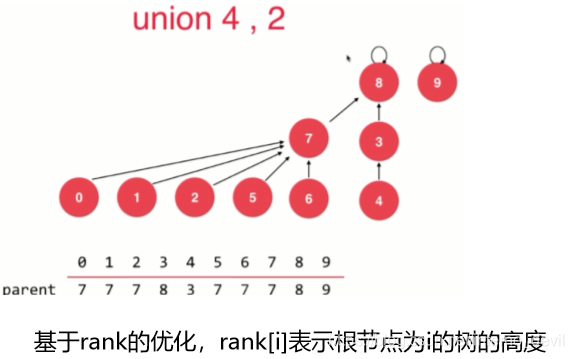
基于rank的优化：

对于此事的并查集而言，如何处理？本身深度为2，按照之前的优化，深度变成4了

Here有一个非常有趣的并查集解读~~欢迎浏览