数据结构---线段树

1.01 线段树

-线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
-使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

1. 一般不考虑增加和删除，只考虑更新和查询，每个结点存储的是一段信息。
   

2. 线段树不一定是满二叉树，也不一定是完全二叉树。
   

3. 线段树一定是一个平衡二叉树（最大深度和最小深度最大相差为1）依然可以用数组表示。。

4. 堆也是一种平衡二叉树，完全二叉树是平衡二叉树，二分搜索树就不一定了。

5. 每个节点以结构体的方式存储，结构体包含以下几个信息：

   区间左端点，右端点（这两者必有）
   这个区间要维护的信息（适实际情况而定，数目不定）

6. 线段树的基本思想：二分

7. 线段树一般结构如图所示：
   
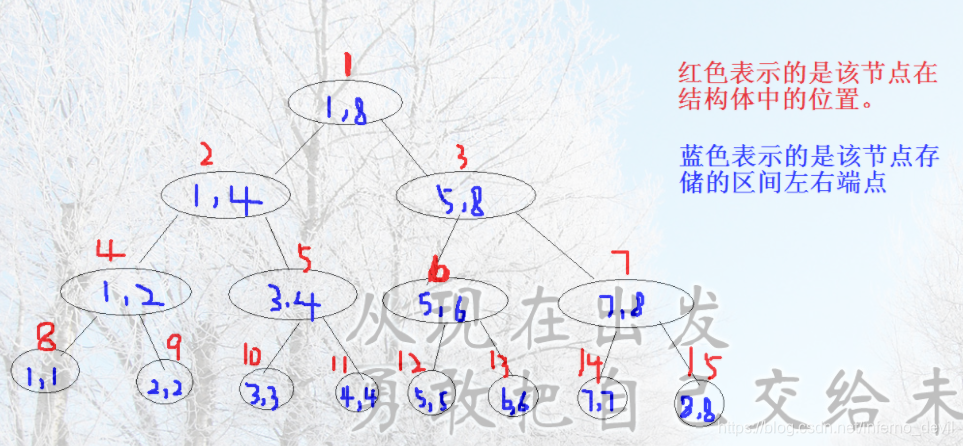
   由上图可知：

   1）每个节点的左孩子区间范围为[1,mid],右孩子为[mid+1,r]
   2)对于节点k,左孩子节点为2k,右孩子为2k+1,这符合完全二叉树的性质

8. 线段树的性质：

   对于满二叉树：

   共有h层的树，一共有2^ h-1个结点（大约2^h）
   第h层的结点个数 2^（h-1）
   最后一层的结点个数大致等于前面所有层结点之和
   

1.02 SegmentTree基于静态数组实现的线段树的定义

1. 定义类

public class SegmentTree<E>

2. 定义成员函数

private E[] tree;
private E[] data;
private Merger<E> merger;
public interface Merger<E>{
	E merge(E a,E b);
}

3. 定义构造函数

public SegmentTree(E[] arr,Merger<E>  merger){
	this.merger=merger;
	data=(E[]) new Object[arr.length];
	for(int i=0;i<arr.length;i++){
		data[i]=arr[i];
	}
	tree=(E[]) new Object[4*arr.length];
	buildSegmentTree(0,0,data.length-1);
}

4. 定义功能

    //获取线段树的大小
    public int getSize(){
    	return data.length;
    }
    
	//获取指定角标index的元素
	public E get(int index){
		if(index<0||index>=data.length){
			throw new IllegalArgumentException("Index is illegal");
		}
		return data[index];
	}
	
	//获取指定角标index的左孩子角标
	private int leftChild(int index){
		return 2*index+1;
	}
	
	//获取指定角标的右孩子角标
	private int rightChild(int index){
		return 2*index+2;
	}
	
	//在treeIndex的位置创建表示区间[1,r]的线段树
	主题思路：
		a)对于二分到的每一个结点，交给它的左右端点确定范围
		b)如果是叶子结点，存储要维护的信息
		c)状态合并
	private  void buildSegmentTree(int treeIndex,int l,int r){
		if(l==r){	//叶子节点
			tree[treeIndex]=data[l];
			return;
		}
		int leftTreeIndex=leftChild(treeIndex);
		int rightTreeIndex=rightChild(treeIndex);
		int mid=l+(r-1)/2;
		buildSegmentTree(leftTreeIndex,l,mid);	//左孩子
		buildSegmentTree(rightTreeIndex,mid+1,r);	//右孩子
		tree[treeIndex]=merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);	//状态合并，此节点的treeIndex=两孩子之和
	}
	
	//返回线段树的字符串表现形式
	public String toString(){
		StringBuilder res=new StringBuilder();
		res.append("[");
		for(int i=0;i<tree.length;i++){
			if(tree[i]!=null){
				res.append(tree[i]);
			}else{
				res.append("null");
			}
			if(i!=tree.length-1){
				res.append(",");
			}else{
				res.append("]");
			}
		}
		return res.tiString();
	}
	
	//在以treeID为根的线段树中更新index的值为e
	private void set(int treeIndex,int l,int r,int index,E e){
		if(l==r){
			tree[treeIndex]=e;
			return;
		}
		int mid=l+(r-1)/2;
		int leftTreeIndex=leftChild(treeIndex);
		int rightTreeIndex=rightChild(treeIndex);
		if(index>=mid+1){
			set(rightTreeIndex,mid+1,r,index,e);
		}else{
			set(leftTreeIndex,l,mid,index,e);
		}
	}

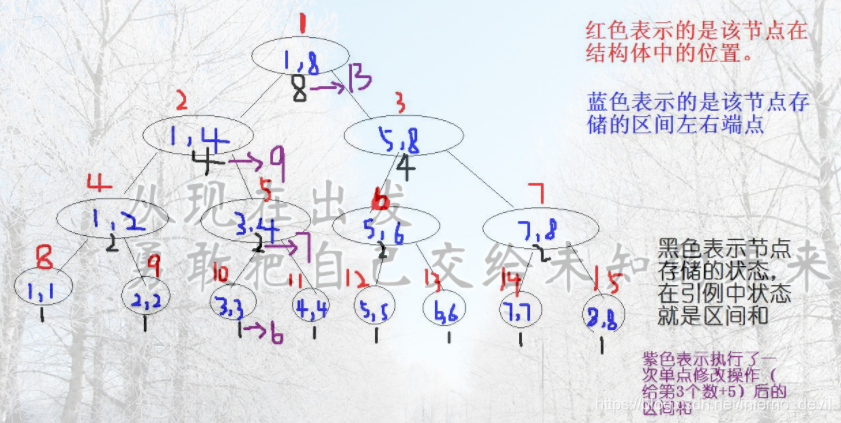
//将index位置的值，更新为e
	主题思想：
		结合单点查询的原理，找到x的位置；
		根据建树状态合并的原理，修改每个节点的状态
	public void set(int index ,E e){
		if(index<0||idex>=data.length){
			throw new IllegalArgumentException("Index is illegal");
		}
		data[index]=e;
		set(0,0,data.length-1.index,e);
	}

	//返回区间[queryL,queryR]的值
	public E query(int queryL,int queryR){
		if(queryL<0||queryL>=data.length||queryR<0||queryR>=data.length||queryL<queryR){
			throw new IllegalArgumentException("index invalid");
		}
		return query(0,0,data.length-1,queryL,queryR);
	}

主题思路：

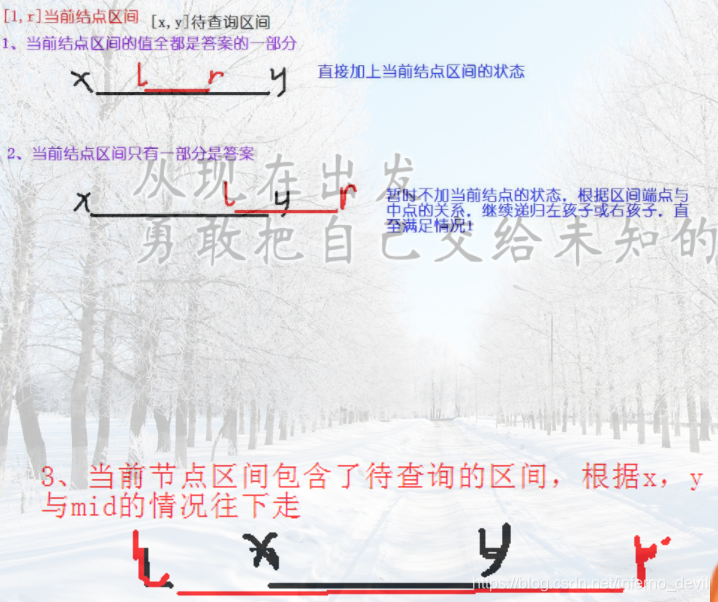
mid=l+(r-1)/2
y<=mid,查询区间全在，当前区间的左子区间，往左孩子走
x>mid,查询区间全在，当前区间的右子区间，往右孩子走
否则，两子区间都走