014——哈夫曼树

于 2025-01-21 14:54:38 发布
阅读量703 收藏 11
点赞数 20
CC 4.0 BY-SA版权
分类专栏： 数据结构 C++ 文章标签： 数据结构 c++ 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/immnature/article/details/145281255

目录

​编辑

概念

相关概念

带权路径长度

构造步骤

性质

应用场景：

代码实现

概念

哈夫曼树（Huffman Tree）是一种用于数据压缩的最优二叉树，基于哈夫曼编码算法构建。它是一种带权路径长度最短的二叉树，常用于文件压缩和编码等场景。

相关概念

带权路径长度

WPL（Weighted Path Length，带权路径长度） 是哈夫曼树的一个重要性质，指的是所有叶子节点的权值与其到根节点路径长度的乘积之和。

公式为：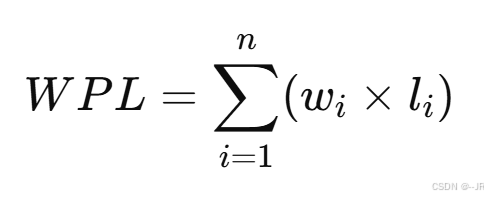

  • wi​: 第 i个叶子节点的权值。
  • li​: 第 i个叶子节点到根节点的路径长度。

哈夫曼树的特点是其 WPL 是最小的，因此被称为最优二叉树。

若想要wpl最小，则让权值越大的结点离根节点更近，所以在构造哈夫曼树的时候，自底向下，让w小的先合并到一起，一次往上构建，即可满足该要求

构造步骤

  1. 将每个权值看作一个节点。
  2. 找出当前权值最小的两个节点，作为左右子节点，构造一个新的父节点。父节点的权值为左右子节点权值之和。
  3. 重复步骤 2，直到所有节点合并成一棵树。

性质

Ⅰ）n个结点合并成一个树需要合并n-1次——>每合并一次需要添加1个结点——>合成一个哈夫曼树需要n-1个结点

Ⅱ）构建的哈夫曼树的wpl是唯一的，但树不唯一

应用场景：

哈夫曼编码：与定长编码不同，哈夫曼编码是一种边长编码，为频率较高的字符分配较短的编码，频率较低的字符分配较长的编码，以节省空间

代码实现

这里我们省略了统计每个字符出现次数的过程，分别用字符数组和权值数组来记录每个字符的权值

char s[105];
int w[105];

为减少不必要麻烦，下标我们这里从0开始

构建结构体存储结点信息

typedef struct {
	int weight;//权值
	//注意，这里存储的是下标信息，所以是int类型
	int left;//左孩子
	int right;//右孩子
	int parent;//父亲
}HuffmanNode,*HuffmanTree;

哈夫曼树的创建

由前面的性质可知，n个数据创建一个哈夫曼树需要m=2n-1个结点，所以在申请大小的时候为m+1个（下标从1开始，所以+1）

HuffmanTree Create_HuffmanTree(int w[], int n) {
    int m = 2 * n - 1; // 哈夫曼树的总节点数
    HuffmanTree tree = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));
    if (!tree) {
        cerr << "内存分配失败" << endl;
        exit(EXIT_FAILURE);
    }

    // 初始化节点
    for (int i = 1; i <= n; i++) {
        tree[i].weight = w[i];
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }
    for (int i = n + 1; i <= m; i++) {
        tree[i].weight = 0;
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }

    // 构造哈夫曼树
    int s1, s2;
    for (int i = n + 1; i <= m; i++) {
        find_Node(tree, i - 1, &s1, &s2);
        tree[i].weight = tree[s1].weight + tree[s2].weight;
        tree[i].left = s1;
        tree[i].right = s2;
        tree[s1].parent = tree[s2].parent = i;
    }
    return tree;
}

// 查找权值最小的两个节点
void find_Node(HuffmanTree tree, int length, int* s1, int* s2) {
    *s1 = *s2 = -1;
    for (int i = 1; i <= length; i++) {
        if (tree[i].parent == 0) { // 未被选择的节点
            if (*s1 == -1 || tree[i].weight < tree[*s1].weight) {
                *s2 = *s1;
                *s1 = i;
            }
            else if (*s2 == -1 || tree[i].weight < tree[*s2].weight) {
                *s2 = i;
            }
        }
    }
}

构建编码的时候，采用的是自底向上的方法，所以这里的start采用的是倒序的形式。而在保存编码这里，一个编码的存储采用一位字符数组，所以多个编码采用了二维字符数组

整体代码：

#define _CRT_SECURE_NO_DEPRECATE

#include <iostream>
#include <cstdlib>
#include <cstring>

using namespace std;

char s[105];     // 存储字符
int w[105];      // 存储权值

typedef struct {
    int weight;  // 权值
    int left;    // 左孩子
    int right;   // 右孩子
    int parent;  // 父亲
} HuffmanNode, * HuffmanTree;

void find_Node(HuffmanTree tree, int length, int* s1, int* s2);
HuffmanTree Create_HuffmanTree(int w[], int n);
char** Create_HuffmanCodes(HuffmanTree tree, int n);

int main() {
    cout << "请输入结点个数：";
    int n;
    cin >> n;

    // 输入字符和对应的权值
    for (int i = 1; i <= n; i++) {
        cin >> s[i] >> w[i];
    }

    // 构造哈夫曼树
    HuffmanTree tree = Create_HuffmanTree(w, n);

    // 输出哈夫曼树的权值
    cout << "哈夫曼树的权值数组：";
    for (int i = 1; i < 2 * n; i++) {
        cout << tree[i].weight << " ";
    }
    cout << endl;

    // 创建哈夫曼编码
    char** codes = Create_HuffmanCodes(tree, n);
    cout << "哈夫曼编码：" << endl;
    for (int i = 1; i <= n; i++) {
        cout << s[i] << ": " << codes[i] << endl;
    }

    // 释放动态分配的内存
    for (int i = 1; i <= n; i++) {
        free(codes[i]);
    }
    free(codes);
    free(tree);

    return 0;
}

// 查找权值最小的两个节点
void find_Node(HuffmanTree tree, int length, int* s1, int* s2) {
    *s1 = *s2 = -1;
    for (int i = 1; i <= length; i++) {
        if (tree[i].parent == 0) { // 未被选择的节点
            if (*s1 == -1 || tree[i].weight < tree[*s1].weight) {
                *s2 = *s1;
                *s1 = i;
            }
            else if (*s2 == -1 || tree[i].weight < tree[*s2].weight) {
                *s2 = i;
            }
        }
    }
}

// 构造哈夫曼树
HuffmanTree Create_HuffmanTree(int w[], int n) {
    int m = 2 * n - 1; // 哈夫曼树的总节点数
    HuffmanTree tree = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));
    if (!tree) {
        cerr << "内存分配失败" << endl;
        exit(EXIT_FAILURE);
    }

    // 初始化节点
    for (int i = 1; i <= n; i++) {
        tree[i].weight = w[i];
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }
    for (int i = n + 1; i <= m; i++) {
        tree[i].weight = 0;
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }

    // 构造哈夫曼树
    int s1, s2;
    for (int i = n + 1; i <= m; i++) {
        find_Node(tree, i - 1, &s1, &s2);
        tree[i].weight = tree[s1].weight + tree[s2].weight;
        tree[i].left = s1;
        tree[i].right = s2;
        tree[s1].parent = tree[s2].parent = i;
    }
    return tree;
}

// 创建哈夫曼编码
char** Create_HuffmanCodes(HuffmanTree tree, int n) {
    char* t = (char*)malloc(n * sizeof(char));
    char** codes = (char**)malloc((n + 1) * sizeof(char*));
    if (!t || !codes) {
        cerr << "内存分配失败" << endl;
        exit(EXIT_FAILURE);
    }

    for (int i = 0; i <= n; i++) {
        codes[i] = NULL;
    }

    for (int i = 1; i <= n; i++) {
        int start = n - 1;
        t[start] = '\0';
        int current = i;
        int parent = tree[i].parent;

        while (parent != 0) {
            start--;
            if (tree[parent].left == current) {
                t[start] = '1';
            }
            else {
                t[start] = '0';
            }
            current = parent;
            parent = tree[current].parent;
        }

        codes[i] = (char*)malloc((n - start) * sizeof(char));
        if (!codes[i]) {
            cerr << "内存分配失败" << endl;
            exit(EXIT_FAILURE);
        }
        strcpy(codes[i], &t[start]);
    }
    free(t);
    return codes;
}

运行结果：

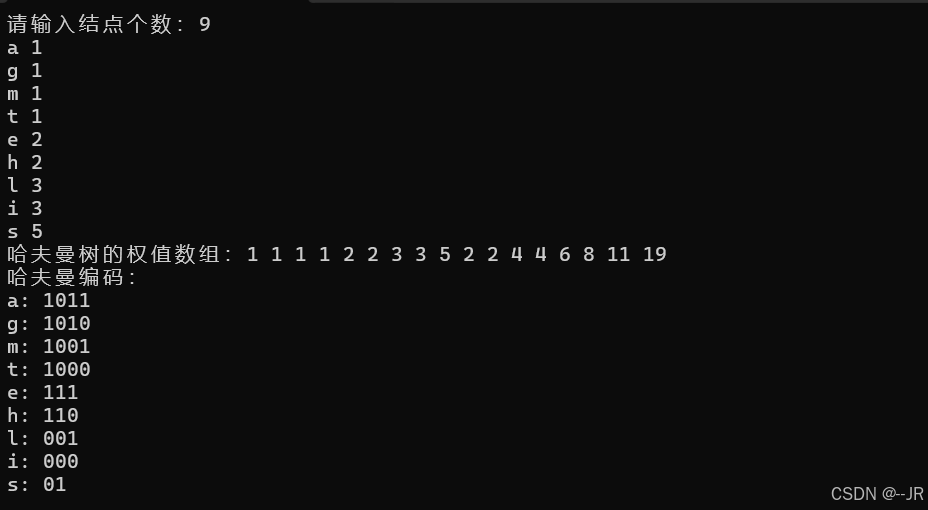
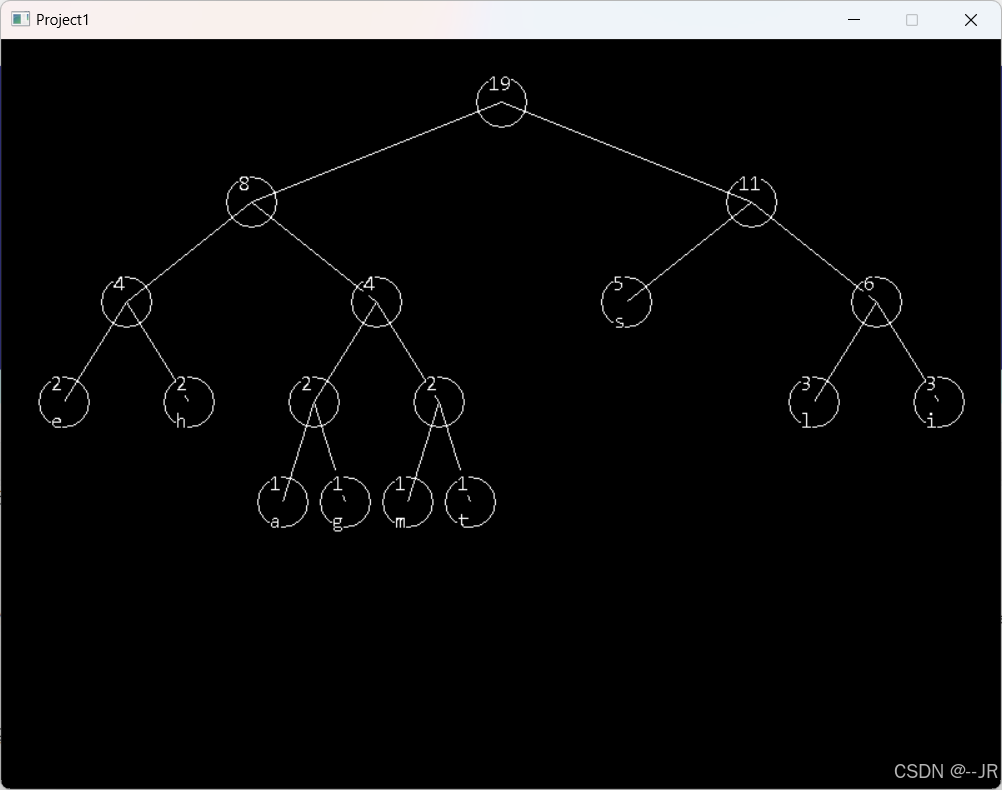
也可以结合easyx库绘制图形

#define _CRT_SECURE_NO_DEPRECATE

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <graphics.h> // 引入 EasyX 库

using namespace std;

char s[105];     // 存储字符
int w[105];      // 存储权值

typedef struct {
    int weight;  // 权值
    int left;    // 左孩子
    int right;   // 右孩子
    int parent;  // 父亲
} HuffmanNode, * HuffmanTree;

void find_Node(HuffmanTree tree, int length, int* s1, int* s2);
HuffmanTree Create_HuffmanTree(int w[], int n);
char** Create_HuffmanCodes(HuffmanTree tree, int n);
void DrawHuffmanTree(HuffmanTree tree, int root, int x, int y, int xOffset, int n);
void DrawTree(HuffmanTree tree, int n);

int main() {
    cout << "请输入结点个数：";
    int n;
    cin >> n;

    // 输入字符和对应的权值
    for (int i = 1; i <= n; i++) {
        cin >> s[i] >> w[i];
    }

    // 构造哈夫曼树
    HuffmanTree tree = Create_HuffmanTree(w, n);

    // 初始化 EasyX 图形窗口
    initgraph(800, 600); // 创建 800x600 的绘图窗口
    settextstyle(20, 0, _T("Consolas")); // 设置字体样式和大小
    cleardevice(); // 清屏

    // 绘制哈夫曼树
    DrawTree(tree, n);

    // 暂停，等待用户关闭窗口
    system("pause");
    closegraph();

    // 输出哈夫曼树的权值
    cout << "哈夫曼树的权值数组：";
    for (int i = 1; i < 2 * n; i++) {
        cout << tree[i].weight << " ";
    }
    cout << endl;

    // 创建哈夫曼编码
    char** codes = Create_HuffmanCodes(tree, n);
    cout << "哈夫曼编码：" << endl;
    for (int i = 1; i <= n; i++) {
        cout << s[i] << ": " << codes[i] << endl;
    }

    // 释放动态分配的内存
    for (int i = 1; i <= n; i++) {
        free(codes[i]);
    }
    free(codes);
    free(tree);

    return 0;
}

// 查找权值最小的两个节点
void find_Node(HuffmanTree tree, int length, int* s1, int* s2) {
    *s1 = *s2 = -1;
    for (int i = 1; i <= length; i++) {
        if (tree[i].parent == 0) { // 未被选择的节点
            if (*s1 == -1 || tree[i].weight < tree[*s1].weight) {
                *s2 = *s1;
                *s1 = i;
            }
            else if (*s2 == -1 || tree[i].weight < tree[*s2].weight) {
                *s2 = i;
            }
        }
    }
}

// 构造哈夫曼树
HuffmanTree Create_HuffmanTree(int w[], int n) {
    int m = 2 * n - 1; // 哈夫曼树的总节点数
    HuffmanTree tree = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));
    if (!tree) {
        cerr << "内存分配失败" << endl;
        exit(EXIT_FAILURE);
    }

    // 初始化节点
    for (int i = 1; i <= n; i++) {
        tree[i].weight = w[i];
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }
    for (int i = n + 1; i <= m; i++) {
        tree[i].weight = 0;
        tree[i].left = tree[i].right = tree[i].parent = 0;
    }

    // 构造哈夫曼树
    int s1, s2;
    for (int i = n + 1; i <= m; i++) {
        find_Node(tree, i - 1, &s1, &s2);
        tree[i].weight = tree[s1].weight + tree[s2].weight;
        tree[i].left = s1;
        tree[i].right = s2;
        tree[s1].parent = tree[s2].parent = i;
    }
    return tree;
}

// 创建哈夫曼编码
char** Create_HuffmanCodes(HuffmanTree tree, int n) {
    char* t = (char*)malloc(n * sizeof(char));
    char** codes = (char**)malloc((n + 1) * sizeof(char*));
    if (!t || !codes) {
        cerr << "内存分配失败" << endl;
        exit(EXIT_FAILURE);
    }

    for (int i = 0; i <= n; i++) {
        codes[i] = NULL;
    }

    for (int i = 1; i <= n; i++) {
        int start = n - 1;
        t[start] = '\0';
        int current = i;
        int parent = tree[i].parent;

        while (parent != 0) {
            start--;
            if (tree[parent].left == current) {
                t[start] = '1';
            }
            else {
                t[start] = '0';
            }
            current = parent;
            parent = tree[current].parent;
        }

        codes[i] = (char*)malloc((n - start) * sizeof(char));
        if (!codes[i]) {
            cerr << "内存分配失败" << endl;
            exit(EXIT_FAILURE);
        }
        strcpy(codes[i], &t[start]);
    }
    free(t);
    return codes;
}

// 绘制哈夫曼树的节点和连接线
void DrawHuffmanTree(HuffmanTree tree, int root, int x, int y, int xOffset, int n) {
    if (root == 0) return;

    // 绘制节点圆形
    circle(x, y, 20);

    // 绘制权值
    wchar_t weightStr[10];
    swprintf(weightStr, 10, L"%d", tree[root].weight);
    outtextxy(x - 10, y - 25, weightStr);

    // 显示字符（仅限叶子节点）
    if (root <= n) {
        wchar_t charStr[10];
        swprintf(charStr, 10, L"%c", s[root]);
        outtextxy(x - 10, y + 5, charStr);
    }

    // 左子树
    if (tree[root].left != 0) {
        int leftX = x - xOffset;
        int leftY = y + 80;
        line(x, y, leftX, leftY); // 绘制连线
        DrawHuffmanTree(tree, tree[root].left, leftX, leftY, xOffset / 2, n);
    }

    // 右子树
    if (tree[root].right != 0) {
        int rightX = x + xOffset;
        int rightY = y + 80;
        line(x, y, rightX, rightY); // 绘制连线
        DrawHuffmanTree(tree, tree[root].right, rightX, rightY, xOffset / 2, n);
    }
}

// 绘制整个哈夫曼树
void DrawTree(HuffmanTree tree, int n) {
    int root = 2 * n - 1; // 哈夫曼树的根节点
    DrawHuffmanTree(tree, root, 400, 50, 200, n); // 居中绘制
}

深度解析哈夫曼树路径问题
主攻整理408、专升本资料~
04-16 161
26考研408数据结构——树与二叉树，持续更新ing
哈夫曼树的介绍：WPL以及路径长度
ZJQ的博客
11-16 2847
Huffman Tree，中文名是哈夫曼树或霍夫曼树，它是最优二叉树。 定义：给定n个权值作为n个叶子结点，构造一棵二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树。 这个定义里面涉及到了几个陌生的概念，下面就是一颗哈夫曼树，我们来看图解答。 (01) 路径和路径长度 定义：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。...
算法中-哈夫曼树（树的带权路径长度（wpl））
ysl1196321875的博客
02-23 5469
哈夫曼树分析+代码+运行结果+概念
【数据结构与算法】哈夫曼树
编程就是在计算机中反应世界
09-12 1402
1. 哈夫曼树的基本概念     哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。     所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为：     WPL=(W1*L1+W2*L2+W3*L3+...+ Wn*Ln)     N个权值Wi(i=1,2,...n)构成一棵有N个
哈夫曼树的WPL值的计算
热门推荐
神様いないの日々
02-22 7万+
在计算WPL值的时候一般是用叶子节点的权值乘上其路径长度，但是实际上在构建哈夫曼树的过程中我们其实已经计算过路径长度了，即 WPL = 哈夫曼树中所有非叶子结点的权值之和 举个例子：构造 1 2 2 5 9的哈夫曼树并计算其WPL值。 上图即为构建出来的HuffmanTree， WPL= （1+2）* 4 + 3 * 2 + 5 * 2 + 9 =37 这个是使用权值乘以路径长度，但是在计算...
哈夫曼树/最优二叉树（WPL）（C语言实现）
BLADCS的博客
05-02 6078
哈夫曼树/最优二叉树（C语言实现） 带长路径长度（WPL）：设二叉树有n个叶子结点，每个叶子结点带有权值Wκ，从根结点到每个叶子结点的长度为lκ，则每个叶子结点的带权路径长度之和就是WPL=∑Wκ•lκ(n,i=1)。 哈夫曼树/最优二叉树：WPL最小二叉树。 举个栗子（WPL） 它的WPL=∑Wκ•lκ(n,i=1)=11+22+33+44+5*4=50 哈夫曼树就是要找WPL最小的树。 哈夫...
【数据结构】-树-计算huffman树的wpl
vector的博客
08-07 1494
wpl=非叶子结点的权值之和 使用上面这个方法的前提是，是一棵huffman树才行，对普通的树没有这个说法。 int wpl = 0; void WPL(BiTree T) { if (T != NULL) { if (T->lchild || T->rchild) wpl=wpl+T->data; WPL(T->lchild); WPL(T->rchild); } } int main() { BiTree T; cout <&lt
WPL、最优二叉树（哈夫曼树）
m0_37976933的博客
04-01 3623
定义：最优树，带全路径长度最短的树 基本概念： 1：路径长度：从树的一个结点到另一个结点的路径中，路径上的分支数目为路径长度 2：树的路径长度：从根结点到某个结点的路径长度之和 3：树的带权路径长度(WPL)：树中所有叶子结点的带权路径长度之和 简单来说：每个（叶子结点的权）（根到该叶子结点的分支数）之和 4：最优二叉树（哈夫曼树）：WPL最小的树 5：一个有n个结点的哈夫曼树共有2n-1个结点 ...
哈工大数据结构大作业——哈夫曼树生成、编码、遍历.doc
最新发布
05-12
哈夫曼编码的过程可以分为几个主要步骤：首先是根据输入的字符及其对应权值生成哈夫曼树，然后通过哈夫曼树来生成最优的0、1编码，最后采用先序、中序、后序等方法遍历哈夫曼树并打印出各节点的权值。 在哈夫曼树的...
C++课程设计——哈夫曼树.txt
04-09
设计内容： 欲发一封内容为AABBCAB ……(共长 100 字符,其中:A 、B 、C 、D 、E 、F分别有7 、9 、12 、22 、23、27个)的电报报文,实现哈夫曼编码。
二叉树的应用——哈夫曼树
筱羊冰冰
08-05 1731
什么是哈夫曼树 很简答啊，是哈夫曼提出来的（雾） 先举一个生活中的例子： 我们都知道考试成绩这东西正常接近于正态分布，那我假设一下 90+占10% 80-90占15% 70-80占25% 60-71占45% 60及以下占5% 然后有一个成绩读入的系统，要统计每一个分数段都有谁，我们可能需要一个switch语句，或者暴力一点if&else，如果我把90+作为比较第一项，那么很多人第一次都不会通过，然后是第二次判断。。把不及格的放在前面也是这个道理。 都知道如果比较的次数多了，时间肯定要长，那么有没
【数据结构】5——哈夫曼树（Huffman Tree）
qq_43507078的博客
09-13 1794
哈夫曼树
最优二叉树——哈夫曼树|最佳编码——哈夫曼编码
diviner_s的博客
05-09 8964
哈夫曼树(最优二叉树) 定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。 路径：从树中一个结点到另一个结点之间得分支构成这两个结点间的路径。 结点的路径长度：两结点间路径上的分支数。 树的路径长度：从树根到每一个结点的路径长度之和。记作：TL...
Huffman树（哈夫曼树）
南方以北
08-17 1万+
哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln)，N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li(i=1,2,...n)。可以...
数据结构期末复习三------哈夫曼树与WPL
2401_83961434的博客
12-20 1020
哈夫曼树又名最优二叉树，指的是当叶子结点带有权值时，通过已知的叶子结点以及相应的权值可以构造出来的带权路径长度最小的二叉树。这就要求权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。
最优二叉树—哈夫曼(huffman)树
一条晒干的咸鱼的博客
10-05 3929
哈夫曼树又称最优二叉树，是一类带权路径长度最短的二叉树，有着广泛的应用。基本概念权：将树中的结点赋上一个有着某种意义的数值路径：从A结点道B结点所经过的分支序列路径长度：从A结点道B结点所经过的分支数目查找效率平均查找长度(ASL)取决于树的高度ASL=(1+2*2+3)/4=2 ASL=(1+2+3...
【数据结构】树的应用-计算哈夫曼树的WPL值
Z_sea的博客
01-09 4688
计算哈夫曼树的WPL值         根据给定的n个权值（非负值），计算所构造哈夫曼树的WPL值。 基本要求：     （1）根据给定的数据，建立哈夫曼树；       （2）输出每个叶子结点的带权路径长度；       （3）输出哈夫曼树的WPL值。 测试数据要求：         输入的n个权值之和应为100，且不允许有负值。  核心代码：   void createhu...
哈夫曼树及求其WPL的算法
Wizzy_Ang的博客
06-30 4304
哈夫曼树及其求其WPL的算法，用AcWing3531. 哈夫曼树作为例题
算法学习笔记——数据结构：哈夫曼树、带权路径长度WPL、哈夫曼编码
Insomnia_X的博客
07-12 2849
树的带权路径长度WPL最小的树为哈夫曼树，本文介绍哈夫曼的构造和应用
实现图像数据的无损压缩——哈夫曼编解码算法
在上述伪代码中，`huffmandict`用于构建哈夫曼树，`huffmanenco`用于编码数据，`encodemat`函数将编码后的数据转换为存储格式，`huffmandeco`则用于解码。 ### 图像数据处理与哈夫曼编码 哈夫曼编码不仅适用于文本...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值