013——并查集

假设有n个互不相交的集合，我们对其有两种操作：合并和查询

举例：

假设有六个集合，分别是{1}、{2}、{3}、{4}、{5}、{6}

操作1：合并1、3所在集合——>{1,3}、{2}、{4}、{5}、{6}

操作2：合并1、6所在集合——>{1,3,6}、{2}、{4}、{5}

操作3：判断3、6是否在同一个集合——>是

查询：

这里可以用一种树型结构进行存储，当两个元素在一个集合中时，用树来表示一个集合，只要他们的根节点时同一个元素，说明两个元素在同一个树上，即在同一个集合中

如何存储：

用一个数组来存储其父亲结点，如f[1]=3,表示元素1的父亲是3

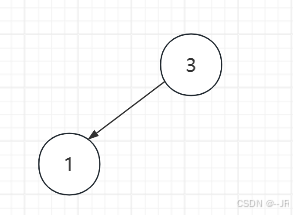
合并：

如集合关系为{1,3,6}、{2，4}、{5}

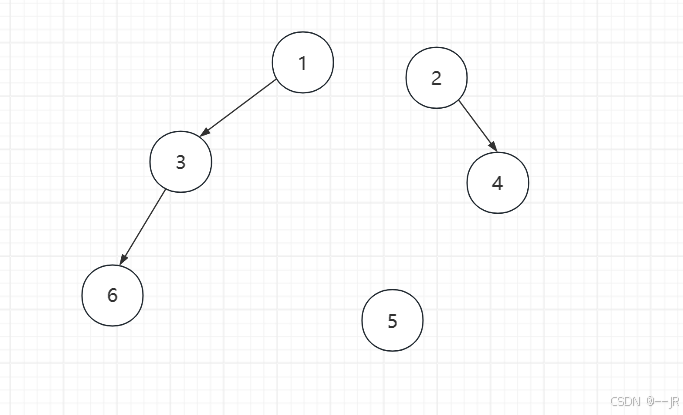
如果想要合并3、2，那么该如何操作？

找到要合并两个元素a、b的根节点为fa、fb，然后让其中一个元素的根节点做另一个元素的根节点的父亲，也就是f [ fa ] = fb,在上一题中就是如下图所示

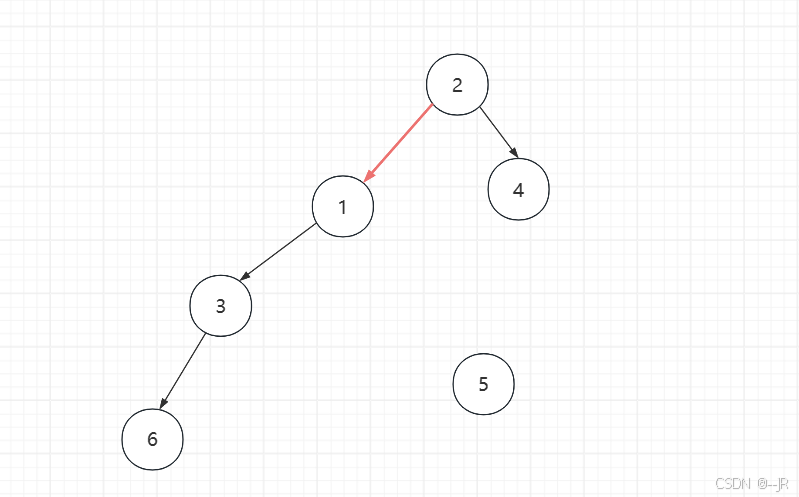
如何查找根节点？

让根节点的元素指向自己，也就是f [a] = a,所以在查询的时候不断跟新a，使得 a = f [a]，直到f [a] == a，说明此时的a就是根节点，具体代码如下：

int find_root(int x) {
	while (f[x] != x) {
		x = f[x];
	}
	return x;
}

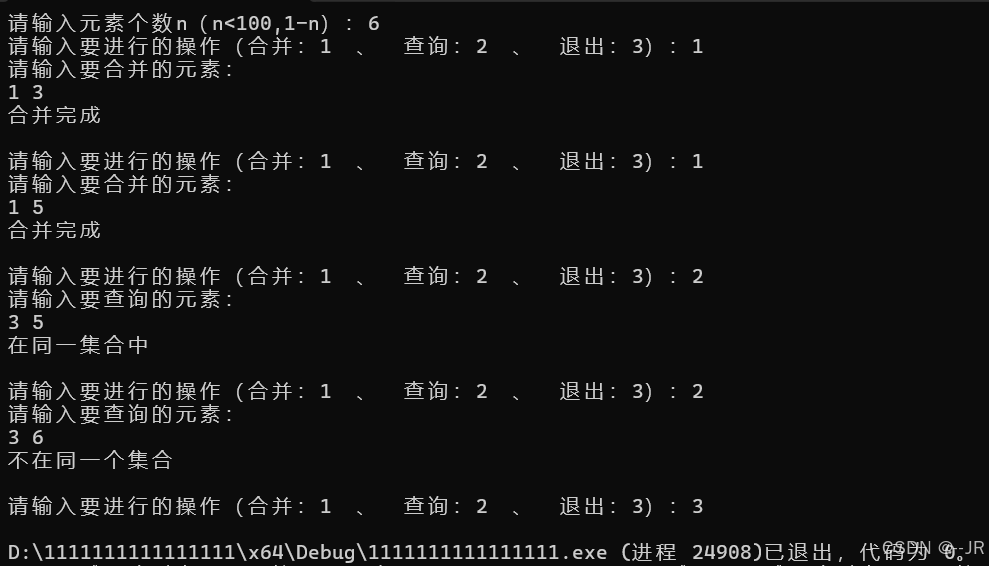
整体代码示例：

#include<iostream>
using namespace std;
int f[100 + 1];
int find_root(int x) {
	while (f[x] != x) {
		x = f[x];
	}
	return x;
}
int main() {
	int n;
	cout << "请输入元素个数n（n<100,1-n）：";
	cin >> n;
	for (int i = 1; i <= n; i++) {
		f[i] = i;
	}
	
	int opt = 0;
	while(opt!=3){
	cout << "请输入要进行的操作（合并：1  、  查询：2  、  退出：3）：";
	opt = 0;
	cin >> opt;
	if (opt == 1) {
		int a = 0, b = 0;
		cout << "请输入要合并的元素：" << endl;
		cin >> a;
		cin >> b;
		int fa = find_root(a);
		int fb = find_root(b);
		if (fa != fb) {
			f[fa] = fb;
			cout << "合并完成" << endl << endl;
		}
		else {
			cout << "俩元素在同一集合中，不需合并" << endl << endl;
		}
	}
	if (opt == 2) {
		int a1 = 0, b1 = 0;
		cout << "请输入要查询的元素：" << endl;
		cin >> a1;
		cin >> b1;
		int fa1 = find_root(a1);
		int fb1 = find_root(b1);
		if (fa1 != fb1) {
			f[fa1] = fb1;
			cout << "不在同一个集合" << endl << endl;
		}
		else {
			cout << "在同一集合中" << endl << endl;
		}
	}

	
	}
	return 0;
}