010——二叉树（2）线索化

引入：

问题1：

n个节点的二叉树，用二叉链表存储，问在这个二叉链表中一共有 __个指针域?
其中，有 __个指针域不为NULL，__个指针域为NULL?

答：2n        n-1        n+1

在二叉链表中，每一个结点都有左右两个指针域，那么有n个结点，则有n个指针域

每一个结点可以有多个孩子，这并不利于我们判断非空指针域个数，所以我们可以考虑每个结点的父亲，因为一个结点的父亲结点有且仅有一个（根节点没有父亲），因此非空指针域为n-1，那么剩下的n+1个指针为空指针

同时这也说明，存在这n+1的指针域空间的浪费

问题2：
中序遍历序列中，E的前驱和后继节点分别是?

一种思路是进行中序遍历（BDCAEHGKF ）保存下中序遍历序列 然后在序列中找某个节点前驱or后继
这里我们还可以采用另一种思路，进行线索化，不需要遍历 直接在树上找答案

那么什么是线索化？

线索化是让一个结点的空左指针指向其前驱结点，让空右指针指向其后继结点。这种指向前驱和后继的指针称为线索。将一棵普通二叉树以某种次序遍历，并添加线索的过程称为线索化

分类

线索化可以分为先序线索化、中序线索化和后序线索化

 例子：中序线索化

在中序遍历的源代码的基础上添加线索，即将之前遍历的visit函数由输出操作改为添加线索操作，引入一个pre指针，记录刚刚访问过的节点。假设现在访问x节点，此时 x的前驱是pre pre的后继是x。如果x->left==NULL x->left=pre;;给x添加前驱线索；如果pre->right==NULL pre->right=x:给pre添加后继线索。在访问完x后 pre=x

中序遍历寻找前驱：

情况1:x-> |flag==1,x的左指针域是线索，x->left就是前驱
情况2:x->lflag==0,x的左指针域是孩子，x的左子树中最靠右的节点是前驱

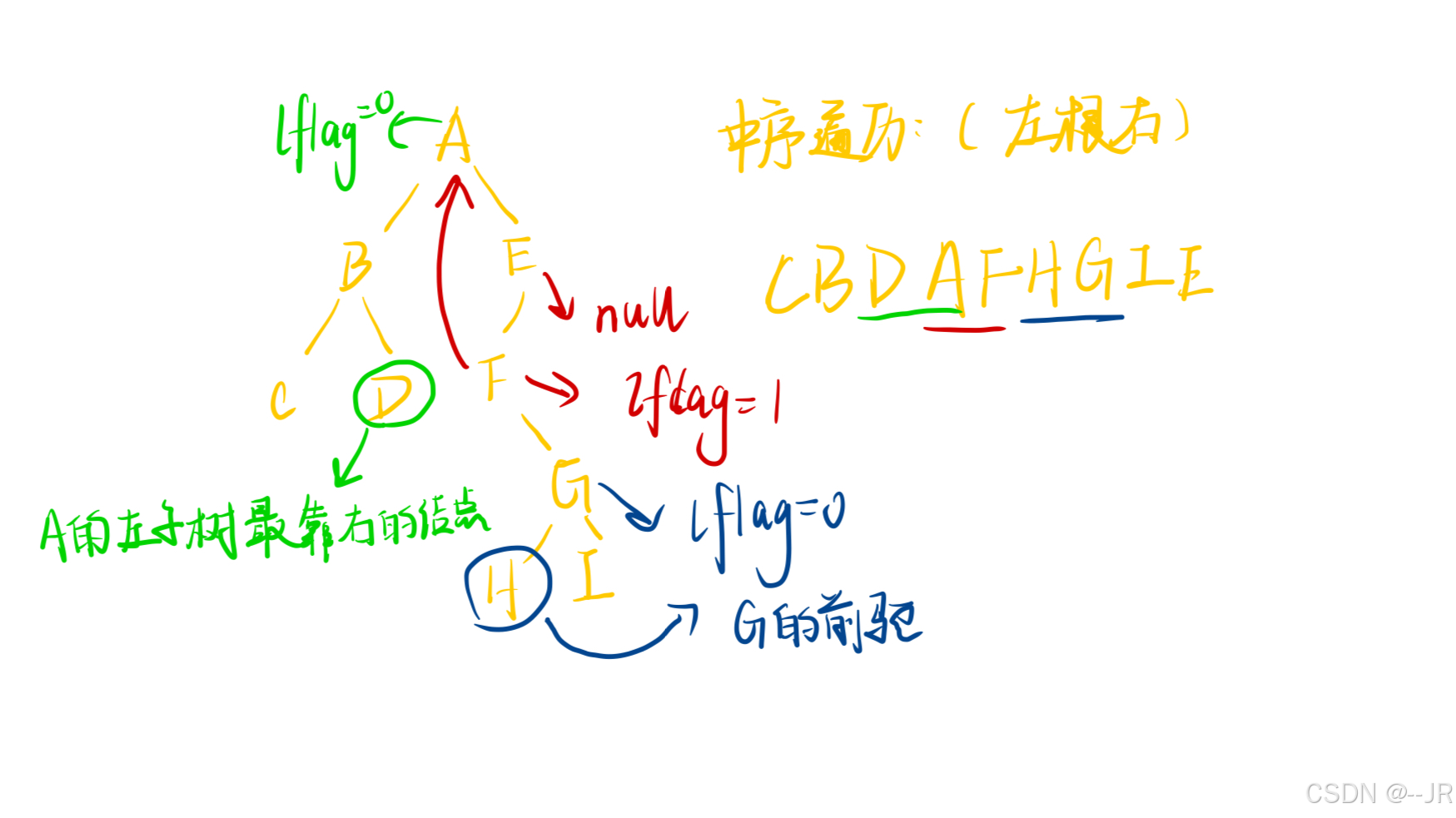
找节点x的中序遍历后继：
情况1：x->rflag==1，x的右指针域是线索，x->rflag就是后继
情况2：x->rFLAG==0，x的右指针域是孩子， 就是后继下右子树中最靠左的节点就是后继

代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

//二叉链表节点结构
typedef struct BTNode {
	char data;
	struct BTNode* left;//保存左孩子地址
	int lflag;//=0 孩子  =1线索 
	struct BTNode* right;//保存右孩子地址 
	int rflag;
}BTNode, * BTree;
BTNode* pre = NULL;
BTree initBTree(char root)
{
	BTNode* r = (BTNode*)malloc(sizeof(BTNode));
	if (r == NULL)
	{
		printf("空间分配失败\n");
		return NULL;
	}
	r->data = root;
	r->left = r->right = NULL;
	r->lflag = r->rflag = 0;
	return r;
}
BTNode* find(BTree r, char fx)
{
	if (r == NULL || r->data == fx)
	{
		return r;
	}

	if (r->left != NULL && r->lflag == 0)
	{
		BTNode* ans = find(r->left, fx);
		if (ans != NULL && ans->data == fx)
		{
			return ans;
		}
	}
	if (r->right != NULL && r->rflag == 0)
	{
		BTNode* ans = find(r->right, fx);
		if (ans != NULL && ans->data == fx)
		{
			return ans;
		}
	}
	return NULL;
}

BTree insert(BTree r, char x, char fx, int flag)
{
	BTNode* f = find(r, fx);
	if (f == NULL)
	{
		printf("父亲节点不存在，不能插入\n");
	}
	else
	{
		BTNode* s = (BTNode*)malloc(sizeof(BTNode));
		//判断s==NULL
		s->data = x;
		s->left = s->right = NULL;
		s->lflag = s->rflag = 0;
		if (flag == 0)
		{
			f->left = s;
		}
		else {
			f->right = s;
		}
	}
	return r;
}
//添加线索 
void visit(BTNode* x)
{

	//pre是x的前驱
	if (x->left == NULL)
	{
		x->left = pre;
		x->lflag = 1;
	}
	//x是pre的后继
	if (pre != NULL && pre->right == NULL)
	{
		pre->right = x;
		pre->rflag = 1;
	}

	pre = x;
}

//对以r为根的树进行先序遍历 
void PerOrder(BTree r)//先序遍历
{
	if (r == NULL)//空树不需要遍历 
	{
		return;
	}

	visit(r);//访问根节点
	if (r->lflag == 0)
		PerOrder(r->left);//对左子树进行先序遍历

	PerOrder(r->right);//对右子树进行先序遍历
}
//对以r为根的树进行中序遍历 
void InOrder(BTree r)//中序遍历
{
	if (r == NULL)//空树不需要遍历 
	{
		return;
	}
	InOrder(r->left);//对左子树进行中序遍历

	visit(r);//访问根节点

	InOrder(r->right);//对右子树进行中序遍历
}
//对以r为根的树进行后序遍历 
void PostOrder(BTree r)//后序遍历
{
	if (r == NULL)//空树不需要遍历 
	{
		return;
	}
	PostOrder(r->left);//对左子树进行后序遍历
	PostOrder(r->right);//对右子树进行后序遍历
	visit(r);//访问根节点
}
BTNode* find_pre(BTree r, BTNode* p)
{
	if (p->lflag == 1)
	{
		return p->left;
	}
	else
	{
		BTNode* q = p->left;
		while (q->right != NULL && q->rflag == 0)
		{
			q = q->right;
		}
		return q;

	}
}
BTNode* find_post(BTree r, BTNode* p)
{
	if (p->rflag == 1)
	{
		return p->right;
	}
	else
	{

		BTNode* q = p->right;
		//如果p是中序遍历序列的最后一个节点，q是NULL；
		if (q == NULL)
		{
			return q;
		}

		while (q->left != NULL && q->lflag == 0)
		{
			q = q->left;
		}
		return q;

	}
}
int main()
{
	int n;
	int flag;//=0 左  =1右孩子 
	BTree r = NULL;
	char root;
	scanf("%d", &n);
	getchar();
	scanf("%c", &root);
	r = initBTree(root);
	char x, fx;
	for (int i = 1; i <= n - 1; i++)
	{
		getchar();
		scanf("%c %c %d", &x, &fx, &flag);
		r = insert(r, x, fx, flag);
	}

	//先序遍历
	//PerOrder(r); 
	//中序遍历s
	InOrder(r);
	getchar();
	scanf("%c", &x);
	BTNode* p = find(r, x);
	//找前驱
	BTNode* ppre = find_pre(r, p);
	if (ppre == NULL)
	{
		printf("中序遍历前驱不存在\n");
	}
	else {
		printf("%c\n", ppre->data);
	}
	//找后继 
	BTNode* post = find_post(r, p);
	if (post == NULL)
	{
		printf("中序遍历后继不存在\n");
	}
	else {
		printf("%c\n", post->data);
	}
	//后序遍历
	//PostOrder(r); 
	return 0;
}