离散时间系统

离散时间系统性质

线性性质的基本概念

线性系统————满足叠加原理的系统

1. 可加性：
   
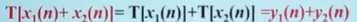
2. 比例性/其次性：
   
   
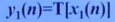
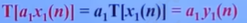
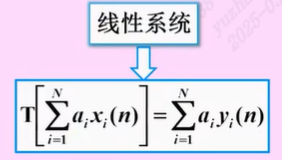
   反褶信号是线性系统
   3点中值滤波器（可以滤掉脉冲型噪声）是非线性系统
   

移不变性质（时不变系统）

若系统响应与激励加于系统的时刻无关，系统为移不变或时不变系统
抽取系统不是时不变系统
y(n) = x(2n)

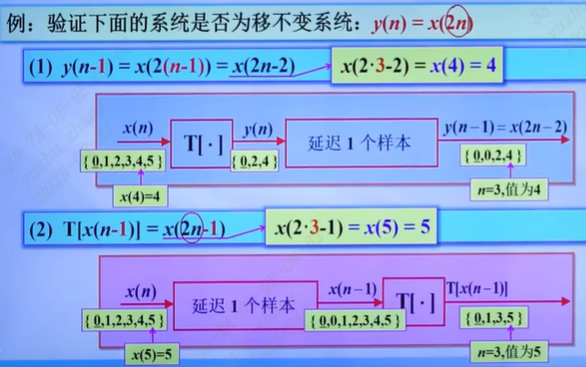
时域求解（LSI系统）

线性卷积

LSI 系统：同时具有线性和移不变性的离散时间系统（Linear Shift Invariant）system

单位冲激（脉冲）响应（h(n)）Impulse Response

当输入为δ(n) 时，系统的输出用h(n)表示。h(n) = T[δ(n)]

线性卷积：卷积（和）：Convolution（sum）

当一个系统是LSI系统时，它的输出y(n)可以用输入x(n)与单位脉冲响应h(n)的线性卷积（卷积和）来表示：y(n) = x(n) * h(n)

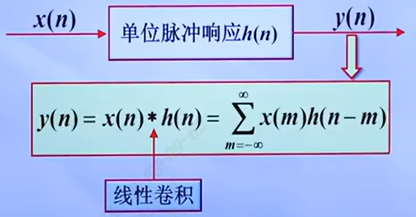
线性卷积的计算方法与步骤

线性卷积2

运算规则

交换律，结合律，分配律

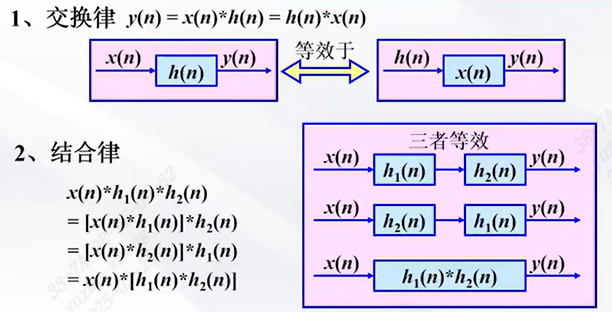
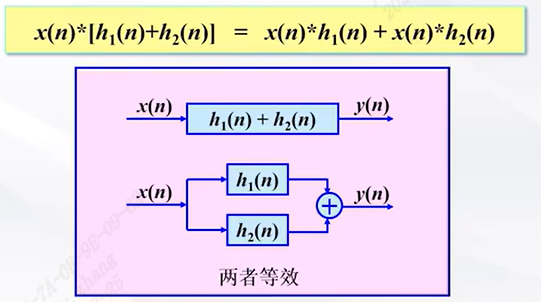
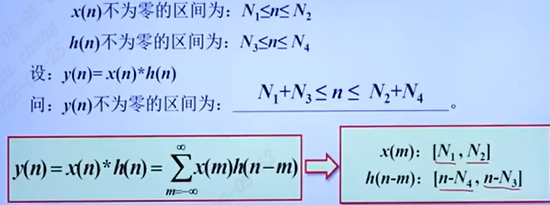
序列的相关

实序列的互相关（cross-correlation）
实序列的自相关（auto-correlation）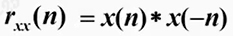

离散时间系统

因果性（causal system）及稳定性

因果性定义

一般系统：某时刻的输出只取决于此时刻和此时刻以前的输入的系统

LSI系统：y(n) = h(n) * x(n), 通过单位脉冲响应判断，如果存在n<0时，h(n)≠0，系统非因果
     若h(n)满足：当n<0时，h(n)=0，此LSI系统为因果系统

稳定性定义

一般系统：有界输入产生有界输出的系统
LSI系统是稳定系统的充分必要条件是：单位脉冲响应绝对可和

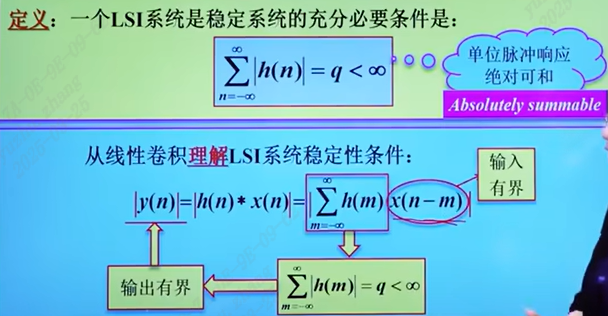
常系数线性差分方程

linear constant-coefficient difference equations

解法：1. 经典解法（类似模拟系统求解微分方程）2. 递推（迭代）3. 变换域（差分方程变换到z域求解）4. 卷积法：由差分方程求出的系统h(n)，再与x(n)卷积