【LeetCode 309】Best Time to Buy and Sell Stock with Cooldown

题意：

股票交易，手里只能持有一股，且卖出以后必须休息一天，不限制总共的交易次数，求能获得的最大利益。

思路：

思路一：
动态规划，涉及到三种状态的状态转移。

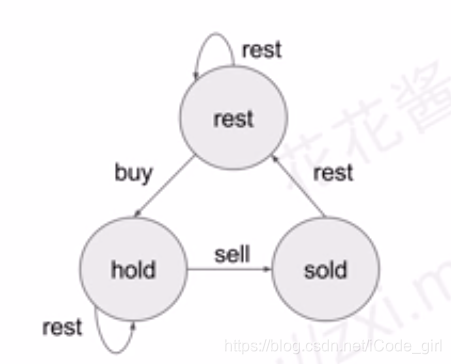
边表示今天的操作。
sold[i] hold[i] rest[i]分别表示第i天操作完成后进入的状态。
那么
sold[i] = hold[i-1] + prices[i]
hold[i] = max(hold[i-1], rest[i-1] - prices[i])
rest[i] = max(rest[i-1], sold[i-1])
时间复杂度O(n)，空间复杂度O(n)，但是当前状态之和前一天状态有关，可以优化到O(1)。
思路二：
自己写的，O（n^2），遍历天数，dp[i]表示第i天能得到的最大收益。
首先遍历第一天到第i-1天，卖掉股票+ 买入股票的-2天的收益，得到第i天卖掉股票的最大收益。
然后dp[i] = max(dp[i], dp[i-1]) 比较得到第i天卖或者不卖的最大收益。
72ms，好歹也过了。。。

代码：

代码一：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.empty() || prices.size() == 1) return 0; 
        int n = prices.size();
        
        #vector<int> rest(n, 0);
        #vector<int> hold(n, 0);
        #vector<int> sold(n, 0);
        
        // init
        int rest[0] = 0;
        hold[0] = -prices[0];
        sold[0] = -INT_MAX;
        
        // transform
        for (int i=1; i<n; ++i) {
            rest[i] = max(sold[i-1], rest[i-1]);
            hold[i] = max(rest[i-1] - prices[i], hold[i-1]);
            sold[i] = hold[i-1] + prices[i];
        }
        
        return max(sold[n-1], rest[n-1]);
    }
};

这个题好难。
参考：https://blog.youkuaiyun.com/zjuPeco/article/details/76468185

代码二：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.empty()) return 0;
        
        int n = prices.size();
        vector<int> dp(n+1, 0);
        
        dp[0] = 0;
        
        for (int i=1; i<n; ++i) {
            for (int j=0; j<i; ++j) {
                dp[i] = max(dp[i], prices[i]-prices[j] + (j>1 ? dp[j-2] : 0));
            }
            dp[i] = max(dp[i], dp[i-1]);
        }
        
        return dp[n-1];
    }
};

思路二是第二次遇见写出来的。。。。。思路一的话，动态规划，重要的是状态转移，应该分析情景中的状态，然后是它们怎么转移的。。。
今天自己写出来了三个media，但是都是一年或半年前做过的，都没有印象了，复杂度都高了一层for循环，一个是两层写了三层，一个是一层写了两层，还都慢悠悠过去了。。。
心好累。。