本文详细解析PAT1009题目，介绍如何找出使等式成立的未知进制，并分享了解题过程中遇到的陷阱及解决方法。
目录
题目描述
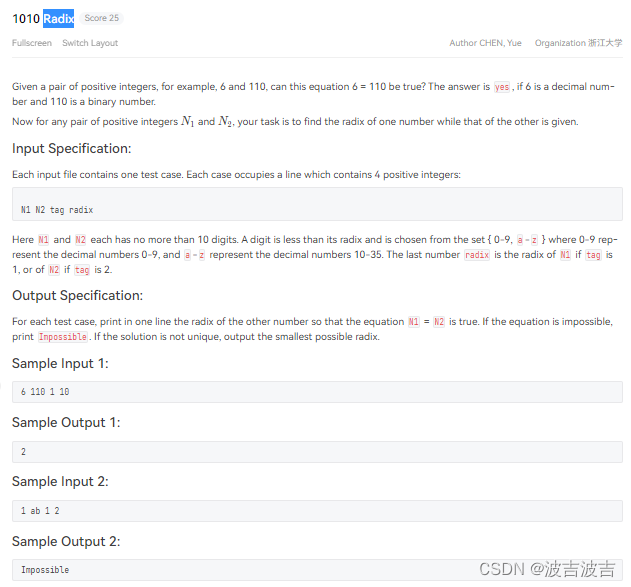
大致意思如下：
输入会给出四个 "数" ,分别是N1,N2,tag,redix
N1、N2是要做比较的数
tag：取值为1或2，标识后面的redix参数是为谁服务的,如果tag = 1，则redix是N1的进制数。
redix：一个正整数，表示某进制，比如redix = 10表示十进制。
也就是说他会给出一个等式 N1 == N2，并告诉你其中一个值是什么进制下的，让你找出另一个数在什么进制下能够使这个等式成立，最后把这个进制输出出来。
如果有多个进制符合，输出最小的那个。如果没有进制符合，输出 "Impossible"
比如第一个例子：
输入：6 110 1 10
即 N1 = 6 ，N2 = 110，告诉你N1 = 6是一个十进制下的数，问你110在什么进制下能和6相等，即有6 == 110
很明显，如果110是个二进制数，那么转化成十进制正好是6，所以2就是我们的答案。
我的解题过程
我的想法很简单，他会给出输入的两个数值，我把已知进制的那个数值先转化成十进制下的，然后再用一个循环，循环的去找另一个数的进制，然后每次循环都求一下在当前进制下转化成十进制能不能使等式成立。
然而，确实是没这么简单的，这道题存在很多的坑，以及恶心的某几个测试用例。
我的这种想法最后只让我得了19分。在摸索中，我找出了某些坑，并拿到了24分，接下来我说下我发现的坑。
最大的一个坑：可能的进制的最大值并不是36
题目里存在一定的误导，题目告诉你N1或者N2的每一位数都可能是 0~9,a~z 并且说了a = 10，z = 35, 我们很容易就想到：既然每一位数最大都不超过35，那最大的进制不就是36进制吗？
恭喜你，完全的错误，大大的踩坑。我一开始就是这么想的，所以我在循环寻找进制的时候，我设置的最大值就是36 ，我的第一次提交以19分作为结束。如下图：
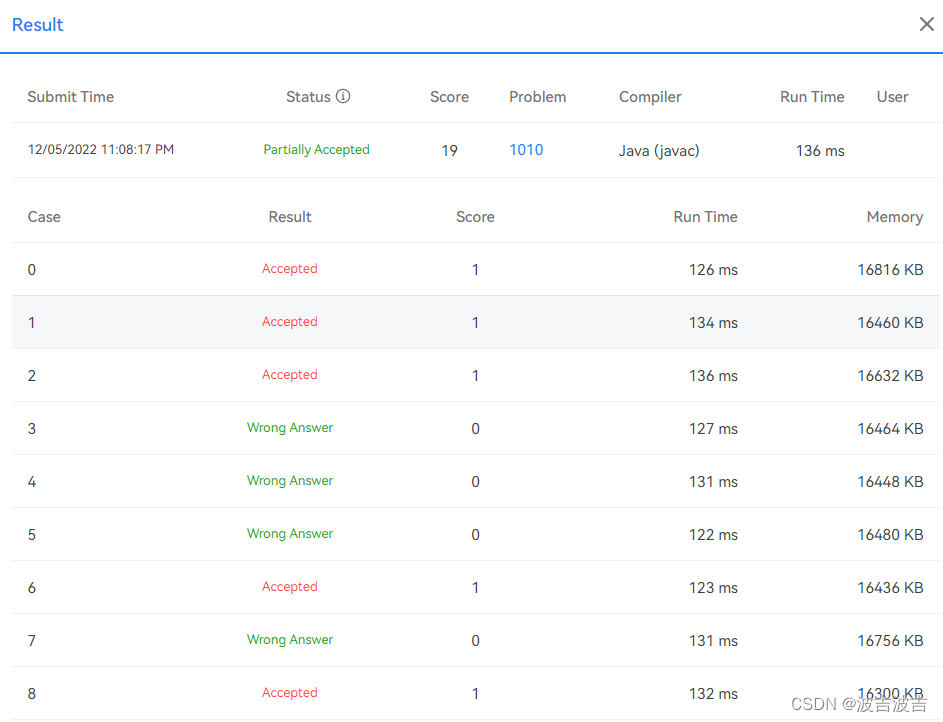
这时的我就很纳闷，觉得自己想的没啥问题，但就是好多的测试点都过不去。此时已经很晚了，我决定第二天再继续想想。
第二天，我准备先仔细看看题目，发现题目中完全没有提到过这个进制的范围，我带着尝试的心理，把循环的次数调大到了100000(随便写的，只是为了调试)。
但是神奇的情况出现了，这次我得了24分，只差一个测试用例就满分ac。
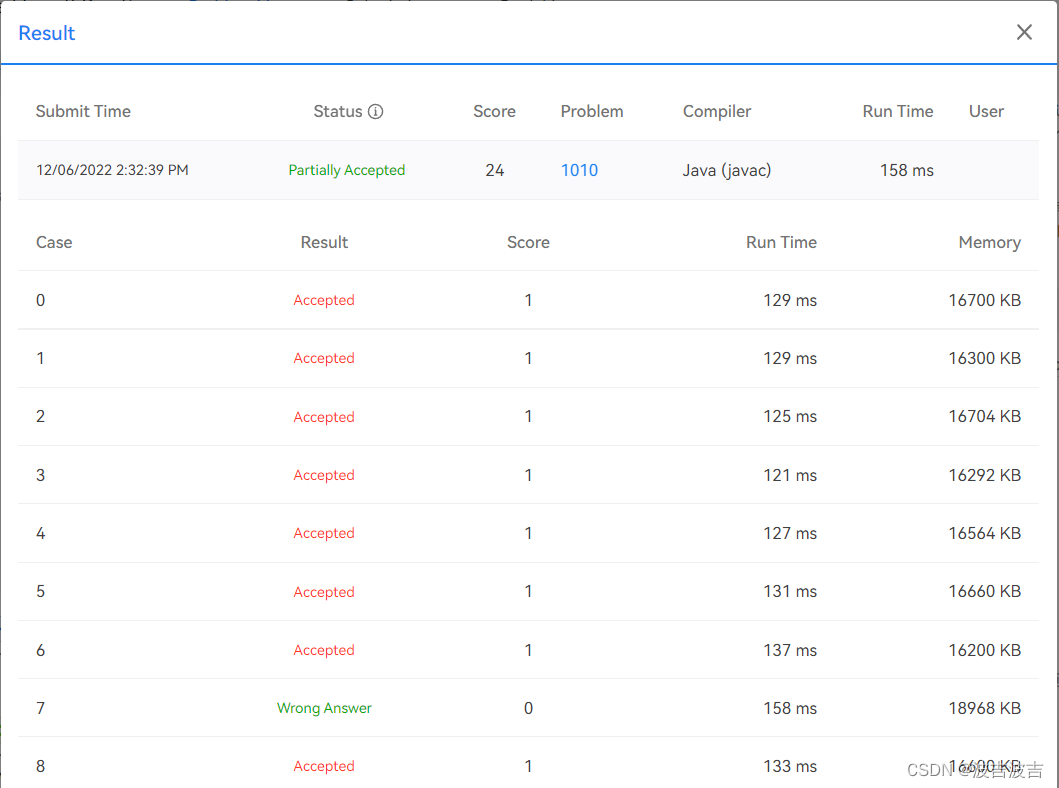
我就知道了，我的最大进制值是100000进制，这个值就已经包含了很多个测试用例的结果。所以我最开始分数低就是因为我踩进坑里，觉得最大进制就是36 。
接下来我就在想，是不是100000不够大，所以才导致我仍然有一个测试点过不去呢？
接下来我又修改了几次最大进制值，当我把循环次数调大到100000000时，第7个测试用例不再是Wrong Answer 而是 Runtime Exceed
那么，是因为我设置的循环次数太多，但是在这么多次循环里，对应进制下的另一个数始终小于已知的那个数，从而导致超时。
那么接下来要做的就是优化这个查找进制的过程，即不要无脑一直循环下去，因为如果他这个测试用例的结果特别特别大，那么你会进行特别特别多次的循环，百分百超时。
所以可以使用二分查找，来减少循环消耗的时间。
不过，既然100000000仍然小，那么int很可能不够用，所以这里把代码中的进制数全改成long类型了。
接下来，出现了第二个坑，修改成二分查找后，再次提交，结果好多以前能通过的测试点现在都通过不了了，因为二分查找的初始上限我用的是long的最大值，那么第一次的mid = (low + high)/2 就很大了，此时去计算每一位会导致直接溢出，long也接不住，而溢出以后是个负数，所以就导致low = mid + 1 ，但很可能我真正的结果是2，3这种很小的数，这不就错过了，到最后一定是错误的值。
但是不用二分法是无法解决最后一个测试点循环次数过多超时的问题的。
于是我做了个筛选，保留原来的100000次循环不变，循环后做个判断，如果最后循环得出的那个最接近目标值的值还是很小，那就从100001开始，low = 100001，而high = long的最大值，这样再去做二分查找，就不会出现漏值的问题了(因为这个测试点一定特别特别大)。也就是单独为这第七个测试点写了个二分查找过程，因为100000已经能够满足其他的测试用例了。
果然，成功AC了。
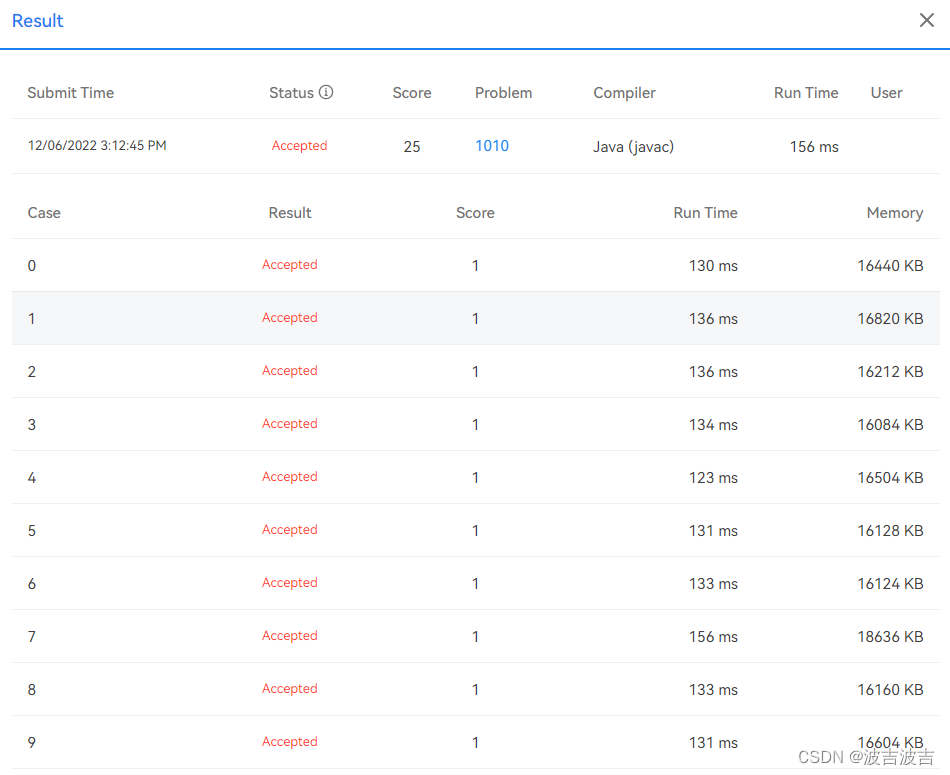
但这是我一次次提交，然后测试并改进得到的最终结果，并不能够在一两次就能直接AC，还是准备去看看别的大佬的思路，或许会有帮助。
实现代码(最终版本)
package com.pat;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
/*
* PAT1009 判断等式是否能成立
* */
// 例如输入 6 110 1 10 意思是 等式左边是6,右边是110,标签= 1代表后面的10是6的进制
// 就是说这个6是10进制下的
// 要求我们输出一个进制数,意思是当不确定进制的那个数是 这个进制下的数的时候, 这个等式就成立了
public class Problem1010 {
// 此方法将传入的某进制下的数字或字母字符串转换成十进制数
public static long toTenRedix(String know,long redix) {
int tempNum = 0;
long i = know.length()-1,result = 0;
for(char temp:know.toCharArray()) {
if(temp>='a'&&temp<='z') {
tempNum = temp - 'a' +10;
}else {
tempNum = temp - '0';
}
// 每一位都不能大于他的进制
if(tempNum>=redix) {
return -1;
}
result += tempNum*Math.pow(redix, i);
i--;
}
//System.out.println(know + ": " +result);
return result;
}
//若输入的N1或N2 是字母串，a = 10,b=11,....,z=35
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String[] N = new String[2];
String know;
long[] a = {0,0};
int tag,redix,tempNum = 0,other;
long result=0;
boolean ifCan = false;
//读入数据
N[0] = scanner.next();
N[1] = scanner.next();
for(int i=0;i<2;i++) {
int index = -1;
//把输入的数据的开头的0都去掉
for(char temp:N[i].toCharArray()) {
if(temp!='0') {
break;
}
index++;
}
if(index==-1) {
//说明这个字符串没有0开头
continue;
}
N[i] = N[i].substring(index+1);
}
tag = scanner.nextInt();
tag = tag - 1;
redix = scanner.nextInt();
//把已知进制的数先记录下来
know = N[tag];
//获取另一个未知进制的数的下标
other = tag==1?0:1;
//把已知转成十进制
a[tag] = toTenRedix(know, redix);
//此题有坑,这里用二分法
for(int r = 1;r<=100000;r++) {
a[other] = toTenRedix(N[other], r);
// 转成十进制后相等了
if(a[other]==a[tag]) {
result = r;
ifCan = true;
break;
}else if(a[other]>a[tag]) {
//现在都比已知的值大了,权重再变大就更大了,不可能相等了
break;
}
}
//为了通过最后一个恶心的测试点
if(a[other]<a[tag]) {
//如果我都把进制调成100000了还是小
//那用二分法开始找
for(long low = 100001,high = Long.MAX_VALUE;low<=high;) {
long mid = (low + high)/2;
a[other] = toTenRedix(N[other], mid);
if(a[other]>a[tag]) {
high = mid - 1;
}else if(a[other]<a[tag]) {
low = mid + 1;
}else {
ifCan = true;
result = mid;
break;
}
}
}
if(ifCan) {
System.out.println(result);
}else {
System.out.println("Impossible");
}
}
}
这题写的真的艰难，不愧是通过率11.33%的题。
主要还是测试点太恶心了，并且还误导我们把36当成最大进制。
这道题并不是一天内ac的，1010打卡失败= =
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
